【自然语言处理】隐马尔科夫模型【Ⅲ】估计问题
有任何的书写错误、排版错误、概念错误等,希望大家包含指正。
由于字数限制,分成六篇博客。
【自然语言处理】隐马尔可夫模型【Ⅰ】马尔可夫模型
【自然语言处理】隐马尔科夫模型【Ⅱ】隐马尔科夫模型概述
【自然语言处理】隐马尔科夫模型【Ⅲ】估计问题
【自然语言处理】隐马尔科夫模型【Ⅳ】学习问题
【自然语言处理】隐马尔科夫模型【Ⅴ】解码问题
【自然语言处理】隐马尔科夫模型【Ⅵ】精度问题
2.3. 估计算法
2.3.1. 直接计算法
给定模型 λ=(A,B,π)\lambda=(A,B, \pi)λ=(A,B,π) 和观测序列 O=(o1,o2,…,oT)O=(o_1, o_2,… , o_T)O=(o1,o2,…,oT),计算观测序列 OOO 出现的概率 P(O∣λ)P(O\mid \lambda)P(O∣λ)。最直接的方法是按概率公式直接计算。通过列举所有可能的长度为 TTT 的状态序列 S=(s1,s2,…,sT)S= (s_1, s_2,\dots,s_T)S=(s1,s2,…,sT),求各个状态序列 SSS 与观测序列 O=(o1,o2,…,oT)O=(o_1,o_2,… ,o_T)O=(o1,o2,…,oT) 的联合概率 P(O,S∣λ)P(O,S \mid \lambda)P(O,S∣λ),然后对所有可能的状态序列求和,得到 P(O∣λ)P(O\mid \lambda)P(O∣λ)。
状态序列 S=(s1,s2,…,sT)S = (s_1,s_2,\dots,s_T)S=(s1,s2,…,sT) 的概率是:
P(S∣λ)=πs1as1s2as2s3…asT−1sT(1)P(S\mid \lambda) = \pi_{s_1}a_{s_1s_2}a_{s_2s_3}\dots a_{s_{T-1}s_T}\tag{1} P(S∣λ)=πs1as1s2as2s3…asT−1sT(1)
式 (1)(1)(1) 可以简洁表示为
P(S∣λ)=πs1∏t=1T−1astst+1P(S\mid \lambda) = \pi_{s_1} \prod_{t=1}^{T-1} a_{s_{t}s_{t+1}} P(S∣λ)=πs1t=1∏T−1astst+1
证明式 (1)(1)(1)。
利用齐次马尔可夫性假设可得,
P(S∣λ)=P(s1,s2,…,sT∣λ)=P(sT∣s1,s2…,sT−1,λ)P(s1,s2,…,sT−1∣λ)=P(sT∣sT−1,λ)P(s1,s2,…,sT−1∣λ)=asT−1sTP(s1,s2,…,sT−1∣λ)\begin{aligned} P(S\mid \lambda) &= P(s_1,s_2,\dots,s_T\mid \lambda) \\ &=P(s_T\mid s_1,s_2\dots, s_{T-1}, \lambda) P(s_1,s_2,\dots,s_{T-1}\mid \lambda) \\ &=P(s_T\mid s_{T-1}, \lambda) P(s_1,s_2,\dots,s_{T-1}\mid \lambda)\\ &=a_{s_{T-1}s_T} P(s_1,s_2,\dots,s_{T-1}\mid \lambda) \end{aligned} P(S∣λ)=P(s1,s2,…,sT∣λ)=P(sT∣s1,s2…,sT−1,λ)P(s1,s2,…,sT−1∣λ)=P(sT∣sT−1,λ)P(s1,s2,…,sT−1∣λ)=asT−1sTP(s1,s2,…,sT−1∣λ)
不妨记 ft=P(s1,s2,…,st∣λ)f_t = P(s_1,s_2,\dots,s_t\mid \lambda)ft=P(s1,s2,…,st∣λ),那么由上式可得递推公式
ft=ft−1⋅ast−1stf_{t} = f_{t-1} · a_{s_{t-1}s_{t}} ft=ft−1⋅ast−1st
又已知 f1=P(s1∣λ)=πs1f_1 = P(s_1\mid \lambda) = \pi_{s_1}f1=P(s1∣λ)=πs1,所以
fT=fT−1⋅asT−1sT=fT−2⋅asT−2sT−1asT−1sT=…=f1⋅as1s2as2s3…asT−1sT=πs1as1s2as2s3…asT−1sT\begin{aligned} f_T &= f_{T-1} · a_{s_{T-1}s_T}\\ &= f_{T-2}·a_{s_{T-2}s_{T-1}} a_{s_{T-1}s_T} \\ &= \dots \\ &= f_1 ·a_{s_1s_2}a_{s_2s_3}\dots a_{s_{T-1}s_T} \\ &= \pi_{s_1}a_{s_1s_2}a_{s_2s_3}\dots a_{s_{T-1}s_T} \end{aligned} fT=fT−1⋅asT−1sT=fT−2⋅asT−2sT−1asT−1sT=…=f1⋅as1s2as2s3…asT−1sT=πs1as1s2as2s3…asT−1sT
即式 (1)(1)(1)。
对固定的状态序列 S=(s1,s2,….,sT)S= (s_1,s_2,…. ,s_T)S=(s1,s2,….,sT),观测序列 O=(o1,o2,…,oT)O=(o_1,o_2,\dots, o_T)O=(o1,o2,…,oT) 的概率是:
P(O∣S,λ)=bs1(o1)bs2(o2)…bsT(oT)(2)P(O\mid S,\lambda) = b_{s_1}(o_1) b_{s_2}(o_2)\dots b_{s_T}(o_T) \tag{2} P(O∣S,λ)=bs1(o1)bs2(o2)…bsT(oT)(2)
式 (2)(2)(2) 可以简洁表示为
P(O∣S,λ)=∏t=1Tbst(ot)P(O\mid S,\lambda) = \prod_{t=1}^T b_{s_t}(o_t) P(O∣S,λ)=t=1∏Tbst(ot)
证明式 (2)(2)(2)。
利用观测独立性假设可得,
P(O∣S,λ)=P(o1,o2,…,oT∣S,λ)=P(oT∣o1,o2,…,oT−1,S,λ)P(o1,o2,…,oT−1∣S,λ)=P(oT∣sT,λ)P(o1,o2,…,oT−1∣S,λ)=bsT(oT)P(o1,o2,…,oT−1∣S,λ)\begin{aligned} P(O\mid S,\lambda) &= P(o_1,o_2,\dots, o_T\mid S,\lambda) \\ &= P(o_T\mid o_1,o_2,\dots, o_{T-1},S,\lambda) P(o_1,o_2,\dots,o_{T-1}\mid S, \lambda) \\ &= P(o_T\mid s_T,\lambda) P(o_1,o_2,\dots, o_{T-1}\mid S, \lambda) \\ &= b_{s_T}(o_T) P(o_1,o_2,\dots, o_{T-1}\mid S, \lambda) \end{aligned} P(O∣S,λ)=P(o1,o2,…,oT∣S,λ)=P(oT∣o1,o2,…,oT−1,S,λ)P(o1,o2,…,oT−1∣S,λ)=P(oT∣sT,λ)P(o1,o2,…,oT−1∣S,λ)=bsT(oT)P(o1,o2,…,oT−1∣S,λ)
不妨记 gt=P(o1,o2,…,ot∣S,λ)g_t = P(o_1,o_2,\dots,o_t\mid S,\lambda)gt=P(o1,o2,…,ot∣S,λ),那么由上式可得递推公式
gt=bst(ot)⋅gt−1g_{t} = b_{s_{t}}(o_{t}) ·g_{t-1} gt=bst(ot)⋅gt−1
又已知 g1=P(o1∣S,λ)=P(o1∣s1,λ)=bs1(o1)g_1 = P(o_1\mid S, \lambda) = P(o_1\mid s_1,\lambda) = b_{s_1}(o_1)g1=P(o1∣S,λ)=P(o1∣s1,λ)=bs1(o1),所以
gT=bsT(oT)⋅gT−1=bsT(oT)bsT−1(oT−1)⋅gT−2=…=bsT(oT)bsT−1(oT−1)…bs2(o2)⋅g1=bsT(oT)bsT−1(oT−1)…bs2(o2)bs1(o1)\begin{aligned} g_T &= b_{s_{T}}(o_T) · g_{T-1}\\ &= b_{s_T}(o_T)b_{s_{T-1}}(o_{T-1}) · g_{T-2} \\ &= \dots \\ &= b_{s_T}(o_T)b_{s_{T-1}}(o_{T-1}) \dots b_{s_2}(o_2) · g_1\\ &= b_{s_T}(o_T)b_{s_{T-1}}(o_{T-1}) \dots b_{s_2}(o_2) b_{s_1}(o_{1}) \end{aligned} gT=bsT(oT)⋅gT−1=bsT(oT)bsT−1(oT−1)⋅gT−2=…=bsT(oT)bsT−1(oT−1)…bs2(o2)⋅g1=bsT(oT)bsT−1(oT−1)…bs2(o2)bs1(o1)
即式 (2)(2)(2)。
OOO 和 SSS 同时出现的联合概率为
P(O,S∣λ)=P(O∣S,λ)P(S∣λ)=πs1∏t=1Tbst(ot)∏t=1T−1astst+1(3)\begin{aligned} P(O,S\mid \lambda) &= P(O\mid S,\lambda) P(S\mid \lambda) \\ &=\pi_{s_1}\prod_{t=1}^T b_{s_t}(o_t)\prod_{t=1}^{T-1} a_{s_{t}s_{t+1}} \tag{3}\\ \end{aligned} P(O,S∣λ)=P(O∣S,λ)P(S∣λ)=πs1t=1∏Tbst(ot)t=1∏T−1astst+1(3)
对所有可能的状态序列 SSS 求和,得到观测序列 OOO 的概率 P(O∣λ)P(O\mid \lambda)P(O∣λ),即
P(O∣λ)=∑SP(O,S∣λ)=∑SP(O∣S,λ)P(S∣λ)=∑s1∑s2⋯∑sT(πs1∏t=1Tbst(ot)∏t=1T−1astst+1)(4)\begin{aligned} P(O\mid \lambda) &=\sum_{S} P(O,S\mid \lambda) \\ &= \sum_{S} P(O\mid S,\lambda)P(S\mid \lambda) \\ &= \sum_{s_1}\sum_{s_2}\dots\sum_{s_T}\left( \pi_{s_1}\prod_{t=1}^T b_{s_t}(o_t)\prod_{t=1}^{T-1} a_{s_{t}s_{t+1}}\right)\tag{4} \\ \end{aligned} P(O∣λ)=S∑P(O,S∣λ)=S∑P(O∣S,λ)P(S∣λ)=s1∑s2∑⋯sT∑(πs1t=1∏Tbst(ot)t=1∏T−1astst+1)(4)
P(O∣λ)P(O\mid \lambda)P(O∣λ) 可以认为是边缘概率,所以有 P(O∣λ)=∑SP(O,S∣λ)P(O\mid \lambda) =\sum\limits_{S} P(O,S\mid \lambda)P(O∣λ)=S∑P(O,S∣λ)。其中,∑S=∑s1∑s2⋯∑sT\sum\limits_S=\sum\limits_{s_1}\sum\limits_{s_2}\dots\sum\limits_{s_T}S∑=s1∑s2∑⋯sT∑ 表示对于每个状态 sis_isi 都枚举其 NNN 种取值情况。
观察式 (4)(4)(4),连加对应的时间复杂度为 O(NT)O(N^T)O(NT),连乘对应的时间复杂度为 O(T)O(T)O(T),所以直接计算法的时间复杂度为 O(TNT)O(TN^T)O(TNT),这种算法显然只在概念上可行,但是在计算上不可行。
不能直接观察出时间复杂度的读者,可以采用写 for 循环的方式计算。一个连加号对应一个 NNN 次枚举的 for 循环,总共 TTT 个这样的循环嵌套,另外,还需要在最内层继续嵌套一个 TTT(或 T−1T-1T−1 次,与具体实现有关)次枚举的 for 循环,该循环的每次枚举都累乘 bst(ot)astst+1b_{s_t}(o_t)a_{s_{t}s_{t+1}}bst(ot)astst+1。可见,总共 T+1T+1T+1 层嵌套循环,最外 TTT 层循环枚举 NNN 次,最内层循环枚举 TTT 次,因此有时间复杂度 O(TNT)O(TN^T)O(TNT)。
2.3.2. 前向算法
前向算法(forward algorithm)是一种基于动态规划(dynamic programming)思想计算 P(O∣λ)P(O\mid \lambda)P(O∣λ) 的算法。
定义前向概率。给定隐马尔可夫模型 λ\lambdaλ,定义到时刻 ttt 部分观测序列为 o1,o2,…,oto_1,o_2,\dots,o_to1,o2,…,ot 且时刻 ttt 对应状态为 qiq_iqi 的概率,记作
αt(i)=P(o1,o2,…,ot,st=qi∣λ)(5)\alpha_t(i) = P(o_1,o_2,\dots, o_t,s_t = q_i\mid \lambda) \tag{5} αt(i)=P(o1,o2,…,ot,st=qi∣λ)(5)
由此可知时刻 TTT 的前向概率为
αT(i)=P(O,sT=qi∣λ)\alpha_T(i) = P(O,s_T = q_i\mid \lambda) αT(i)=P(O,sT=qi∣λ)
因此
P(O∣λ)=∑i=1NP(O,sT=qi∣λ)=∑i=1NαT(i)(6)P(O\mid \lambda) = \sum_{i=1}^N P(O,s_T=q_i\mid \lambda) = \sum_{i=1}^N \alpha_T(i)\tag{6} P(O∣λ)=i=1∑NP(O,sT=qi∣λ)=i=1∑NαT(i)(6)
特别地,时刻 111 的前向概率为
α1(i)=P(o1,s1=qi∣λ)=P(o1∣s1=qi,λ)P(s1=qi∣λ)=bi(o1)πi(7)\begin{aligned} \alpha_1(i) &= P(o_1,s_1 = q_i\mid \lambda) \\ &= P(o_1\mid s_1 = q_i, \lambda) P(s_1 = q_i\mid \lambda) \\ &= b_i(o_1)\pi_i \tag{7} \end{aligned} α1(i)=P(o1,s1=qi∣λ)=P(o1∣s1=qi,λ)P(s1=qi∣λ)=bi(o1)πi(7)
动态规划问题的三个要素,状态保存、状态转移和边界条件。式 (5)(5)(5) 指明了状态保存的方式,式 (6)(6)(6) 和 (7)(7)(7) 为边界条件,其中式 (6)(6)(6) 为目标,式 (7)(7)(7) 为初值。还缺少状态转移部分,即递推公式。
利用齐次马尔可夫性假设和观测独立性假设可得,
αt+1(i)=P(o1,o2,…,ot+1,st+1=qi∣λ)=∑j=1NP(o1,o2,…,ot+1,st=qj,st+1=qi∣λ)=∑j=1NP(ot+1∣o1,o2,…,ot,st=qj,st+1=qi,λ)P(o1,o2,…,ot,st=qj,st+1=qi∣λ)=∑j=1NP(ot+1∣st+1=qi,λ)P(o1,o2,…,ot,st=qj,st+1=qi∣λ)=[∑j=1NP(st+1=qi∣o1,o2,…,ot,st=qj,λ)P(o1,o2,…,ot,st=qj∣λ)]P(ot+1∣st+1=qi,λ)=[∑j=1NP(st+1=qi∣st=qj,λ)P(o1,o2,…,ot,st=qj∣λ)]P(ot+1∣st+1=qi,λ)=[∑j=1Najiαt(j)]bi(ot+1)(8)\begin{aligned} \alpha_{t+1}(i) &= P(o_1,o_2,\dots,o_{t+1},s_{t+1}=q_i\mid \lambda) \\ &=\sum_{j=1}^N P(o_1,o_2,\dots,o_{t+1},s_t = q_j,s_{t+1}=q_i\mid \lambda) \\ &=\sum_{j=1}^N P(o_{t+1}\mid o_1,o_2,\dots,o_{t},s_t = q_j,s_{t+1}=q_i,\lambda) P(o_1,o_2,\dots,o_{t},s_t = q_j,s_{t+1}=q_i\mid \lambda) \\ &=\sum_{j=1}^N P(o_{t+1}\mid s_{t+1}=q_i,\lambda) P(o_1,o_2,\dots,o_{t},s_t = q_j,s_{t+1}=q_i\mid \lambda) \\ &= \left[\sum_{j=1}^N P(s_{t+1} = q_i\mid o_1,o_2,\dots,o_{t},s_t = q_j,\lambda) P(o_1,o_2,\dots,o_{t},s_t = q_j\mid \lambda)\right]P(o_{t+1}\mid s_{t+1}=q_i,\lambda) \\ &= \left[\sum_{j=1}^N P(s_{t+1} = q_i\mid s_t = q_j,\lambda) P(o_1,o_2,\dots,o_{t},s_t = q_j\mid \lambda)\right]P(o_{t+1}\mid s_{t+1}=q_i,\lambda) \\ &=\left[\sum_{j=1}^Na_{ji}\alpha_t(j)\right]b_i(o_{t+1})\tag{8} \end{aligned} αt+1(i)=P(o1,o2,…,ot+1,st+1=qi∣λ)=j=1∑NP(o1,o2,…,ot+1,st=qj,st+1=qi∣λ)=j=1∑NP(ot+1∣o1,o2,…,ot,st=qj,st+1=qi,λ)P(o1,o2,…,ot,st=qj,st+1=qi∣λ)=j=1∑NP(ot+1∣st+1=qi,λ)P(o1,o2,…,ot,st=qj,st+1=qi∣λ)=[j=1∑NP(st+1=qi∣o1,o2,…,ot,st=qj,λ)P(o1,o2,…,ot,st=qj∣λ)]P(ot+1∣st+1=qi,λ)=[j=1∑NP(st+1=qi∣st=qj,λ)P(o1,o2,…,ot,st=qj∣λ)]P(ot+1∣st+1=qi,λ)=[j=1∑Najiαt(j)]bi(ot+1)(8)
完整算法如下。
输入:隐马尔科夫模型λ,观测序列O过程:\begin{array}{ll} \textbf{输入:}&\space隐马尔科夫模型 \space\lambda,\space 观测序列\space O &&& \\ \textbf{过程:} \end{array} 输入:过程: 隐马尔科夫模型 λ, 观测序列 O
1:fori=1,2,…,Ndo2:α1(i)=πibi(o1);3:endfor4:fort=1,2,…,T−1do5:fori=1,2,…,Ndo6:αt+1(i)=[∑j=1Najiαt(j)]bi(ot+1);7:endfor8:endfor9:P=0;10:fori=1,2,…,Ndo11:P=P+αT(i);12:endfor\begin{array}{rl} 1:& \textbf{for}\space i = 1,2,\dots,N \space\textbf{do} \\ 2:& \space\space\space\space \alpha_1(i)=\pi_ib_i(o_1)\space; \\ 3:& \textbf{end} \space \textbf{for} \\ 4:& \textbf{for}\space t = 1,2,\dots,T-1 \space\textbf{do} \\ 5:& \space\space\space\space \textbf{for}\space i = 1,2,\dots,N \space\textbf{do} \\ 6:& \space\space\space\space\space\space\space\space \alpha_{t+1}(i)=\left[\sum\limits_{j=1}^Na_{ji}\alpha_t(j)\right]b_i(o_{t+1}) \space ;\\ 7:& \space\space\space\space \textbf{end} \space \textbf{for} \\ 8:& \textbf{end} \space \textbf{for} \\ 9:& P = 0\space; \\ 10:& \textbf{for}\space i = 1,2,\dots,N \space\textbf{do} \\ 11:& \space\space\space\space P=P+\alpha_T(i)\space; \\ 12:& \textbf{end} \space \textbf{for} \\ \end{array} 1:2:3:4:5:6:7:8:9:10:11:12:for i=1,2,…,N do α1(i)=πibi(o1) ;end forfor t=1,2,…,T−1 do for i=1,2,…,N do αt+1(i)=[j=1∑Najiαt(j)]bi(ot+1) ; end forend forP=0 ;for i=1,2,…,N do P=P+αT(i) ;end for
输出:观测序列概率P\begin{array}{l} \textbf{输出:}\space 观测序列概率\space P &&&&&&&&&& \end{array} 输出: 观测序列概率 P
算法 1 观测序列概率的前向算法
如图 222 所示,前向算法实际是基于“状态序列的路径结构”递推计算 P(O∣λ)P(O\mid \lambda)P(O∣λ) 的算法。前向算法高效的关键是其局部计算前向概率,然后利用路径结构将前向概率“递推”到全局,得到 P(O∣λ)P(O\mid\lambda)P(O∣λ)。具体地,在时刻 t=1t = 1t=1,计算 α1(i)α_1(i)α1(i) 的 NNN 个值 (i=1,2,…,N)(i=1,2,\dots, N)(i=1,2,…,N);在各个时刻 t=1,2,…,T−1t=1,2,\dots,T-1t=1,2,…,T−1,计算 αt+1(i)\alpha_{t+1}(i)αt+1(i) 的 NNN 个值 (i=1,2,…,N)(i=1,2,\dots, N)(i=1,2,…,N),而且每个 αt+1(i)\alpha_{t+1}(i)αt+1(i) 的计算利用前一时刻 NNN 个 αt(j)\alpha_t(j)αt(j)。减少计算量的原因在于每一次计算直接引用前一个时刻的计算结果,避免重复计算。这样,利用前向概率计算 P(O∣λ)P(O\mid \lambda)P(O∣λ) 的时间复杂度为 O(TN2)O(TN^2)O(TN2),显然比直接计算的时间复杂度 O(TNT)O(TN^T)O(TNT) 要小。
图 2 前向算法动态计算过程(详)
我们也可以通过类似图 111 所展示的模型结构,来抽象地理解前向概率的定义以及前向算法的动态计算过程,如图 333 所示。
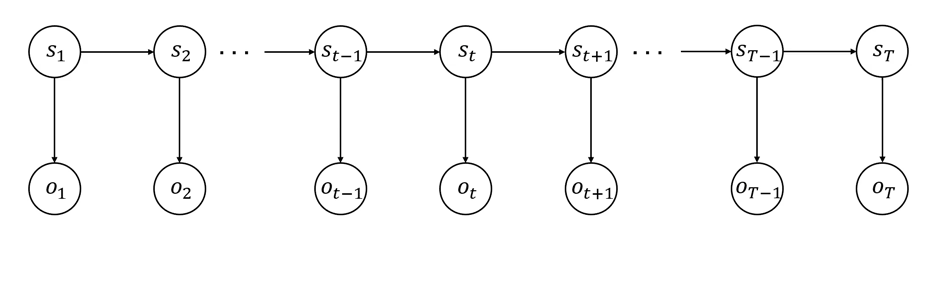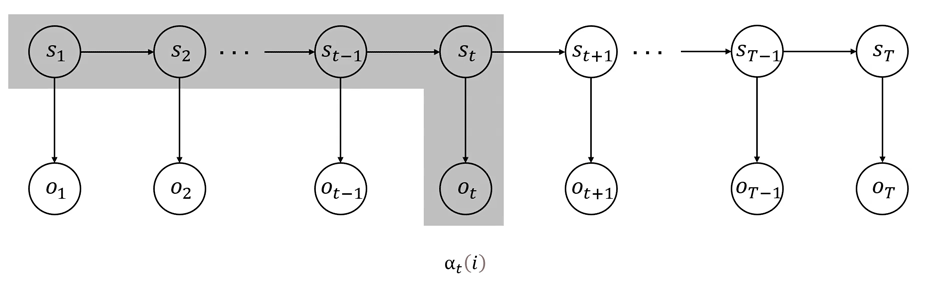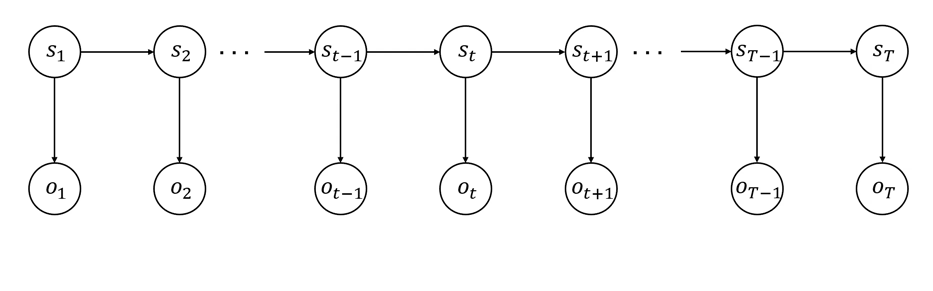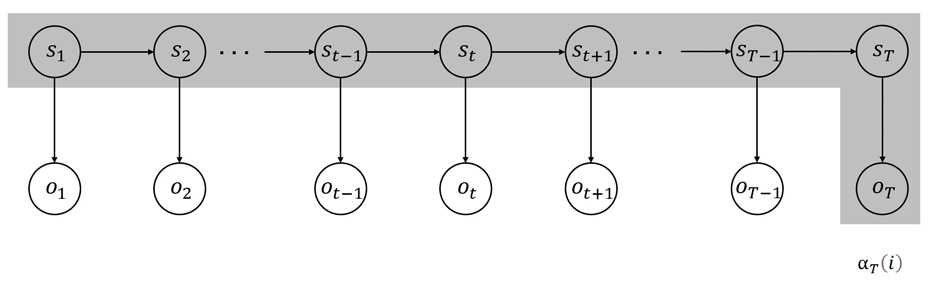
图 3 前向算法动态计算过程(简)
通过例子来理解前向算法的计算过程。考虑盒子与球模型 λ=(A,B,π)\lambda = (A,B,\pi)λ=(A,B,π),状态集合 Q={1,2,3}Q=\{1,2,3\}Q={1,2,3},观测集合 V={V = \{V={红,,, 白}\}},
A=[0.50.20.30.30.50.20.20.30.5],B=[0.50.50.40.60.70.3],π=[0.20.40.4]A = \left[\begin{matrix} 0.5 & 0.2 & 0.3 \\ 0.3 & 0.5 & 0.2 \\ 0.2 & 0.3 & 0.5 \\ \end{matrix}\right],\space\space\space\space B = \left[\begin{matrix} 0.5 & 0.5 \\ 0.4 & 0.6 \\ 0.7 & 0.3 \\ \end{matrix}\right],\space\space\space\space \pi = \left[\begin{matrix} 0.2 \\ 0.4 \\ 0.4 \\ \end{matrix}\right] A=⎣⎡0.50.30.20.20.50.30.30.20.5⎦⎤, B=⎣⎡0.50.40.70.50.60.3⎦⎤, π=⎣⎡0.20.40.4⎦⎤
设 T=3T=3T=3,O=(O = (O=(红,,, 白,,, 红))),用前向算法计算 P(O∣λ)P(O\mid \lambda)P(O∣λ) 如下。
计算初值
α1(1)=π1b1(o1)=0.2×0.5=0.10α1(2)=π2b2(o1)=0.4×0.4=0.16α1(3)=π3b3(o1)=0.4×0.7=0.28\alpha_1(1) = \pi_1b_1(o_1) = 0.2 \times 0.5 = 0.10 \\ \alpha_1(2) = \pi_2b_2(o_1) = 0.4 \times 0.4 = 0.16 \\ \alpha_1(3) = \pi_3b_3(o_1) = 0.4 \times 0.7 = 0.28 \\ α1(1)=π1b1(o1)=0.2×0.5=0.10α1(2)=π2b2(o1)=0.4×0.4=0.16α1(3)=π3b3(o1)=0.4×0.7=0.28
递推计算
α2(1)=[∑i=13α1(i)ai1]b1(o2)=0.154×0.5=0.0770α2(2)=[∑i=13α1(i)ai2]b2(o2)=0.184×0.6=0.1104α2(3)=[∑i=13α1(i)ai3]b3(o2)=0.202×0.3=0.0606\alpha_2(1) = \left[ \sum_{i=1}^3\alpha_1(i)a_{i1} \right]b_1(o_2) = 0.154\times 0.5 = 0.0770 \\ \alpha_2(2) = \left[ \sum_{i=1}^3\alpha_1(i)a_{i2} \right]b_2(o_2) = 0.184\times 0.6 = 0.1104 \\ \alpha_2(3) = \left[ \sum_{i=1}^3\alpha_1(i)a_{i3} \right]b_3(o_2) = 0.202\times 0.3 = 0.0606 \\ α2(1)=[i=1∑3α1(i)ai1]b1(o2)=0.154×0.5=0.0770α2(2)=[i=1∑3α1(i)ai2]b2(o2)=0.184×0.6=0.1104α2(3)=[i=1∑3α1(i)ai3]b3(o2)=0.202×0.3=0.0606
α3(1)=[∑i=13α2(i)ai1]b1(o3)=0.04187α3(2)=[∑i=13α2(i)ai2]b2(o3)=0.03551α3(3)=[∑i=13α2(i)ai3]b3(o3)=0.05284\alpha_3(1) = \left[ \sum_{i=1}^3\alpha_2(i)a_{i1} \right]b_1(o_3) = 0.04187\\ \alpha_3(2) = \left[ \sum_{i=1}^3\alpha_2(i)a_{i2} \right]b_2(o_3) = 0.03551\\ \alpha_3(3) = \left[ \sum_{i=1}^3\alpha_2(i)a_{i3} \right]b_3(o_3) = 0.05284\\ α3(1)=[i=1∑3α2(i)ai1]b1(o3)=0.04187α3(2)=[i=1∑3α2(i)ai2]b2(o3)=0.03551α3(3)=[i=1∑3α2(i)ai3]b3(o3)=0.05284
最终计算出 P(O∣λ)P(O\mid\lambda)P(O∣λ)
P(O∣λ)=∑i=13α3(i)=0.13022P(O\mid \lambda) = \sum_{i=1}^3 \alpha_3(i) = 0.13022 P(O∣λ)=i=1∑3α3(i)=0.13022
2.3.3. 后向算法
后向算法也是基于动态规划的思想降低时间复杂度,与前向算法不同之处在于后向算法是从时刻 TTT 向时刻 111 递推计算的。
定义后向概率。 给定隐马尔可夫模型 λ\lambdaλ,定义在时刻 ttt 状态为 qiq_iqi 的条件下,从 t+1t+1t+1 到 TTT 的部分观测序列为 ot+1,ot+2,…,oTo_{t+1},o_{t+2},\dots,o_{T}ot+1,ot+2,…,oT 的概率为后向概率,记作
βt(i)=P(ot+1,ot+2,…,oT∣st=qi,λ)(9)\beta_t(i) = P(o_{t+1},o_{t+2},\dots, o_T\mid s_t = q_i,\lambda)\tag{9} βt(i)=P(ot+1,ot+2,…,oT∣st=qi,λ)(9)
后向算法的初始化为
βT(i)=1,1≤i≤N\beta_T(i) = 1,\space\space\space\space 1\le i \le N \\ βT(i)=1, 1≤i≤N
利用观测独立性假设可得 P(O∣λ)P(O\mid \lambda)P(O∣λ)
P(O∣λ)=∑i=1NP(O,s1=qi∣λ)=∑i=1NP(O∣s1=qi,λ)P(s1=qi∣λ)=∑i=1NP(o1∣o2,o3,…,oT,s1=qi,λ)P(o2,o3,…,oT∣s1=qi)P(s1=qi∣λ)=∑i=1NP(o1∣s1=qi,λ)P(o2,o3,…,oT∣s1=qi)P(s1=qi∣λ)=∑i=1Nbi(o1)β1(i)πi(10)\begin{aligned} P(O\mid \lambda) &= \sum_{i=1}^N P(O,s_1 = q_i\mid \lambda)\\ &= \sum_{i=1}^N P(O\mid s_1 = q_i, \lambda) P(s_1 = q_i\mid \lambda) \\ &= \sum_{i=1}^N P(o_1\mid o_2,o_3,\dots, o_T, s_1 = q_i, \lambda) P(o_2,o_3,\dots, o_T\mid s_1 = q_i) P(s_1 = q_i\mid \lambda) \\ &= \sum_{i=1}^N P(o_1\mid s_1 = q_i, \lambda) P(o_2,o_3,\dots, o_T\mid s_1 = q_i) P(s_1 = q_i\mid \lambda) \\ &= \sum_{i=1}^N b_i(o_1) \beta_1(i) \pi_i \tag{10} \end{aligned} P(O∣λ)=i=1∑NP(O,s1=qi∣λ)=i=1∑NP(O∣s1=qi,λ)P(s1=qi∣λ)=i=1∑NP(o1∣o2,o3,…,oT,s1=qi,λ)P(o2,o3,…,oT∣s1=qi)P(s1=qi∣λ)=i=1∑NP(o1∣s1=qi,λ)P(o2,o3,…,oT∣s1=qi)P(s1=qi∣λ)=i=1∑Nbi(o1)β1(i)πi(10)
推导递推公式,
βt(i)=P(ot+,ot+2,…,oT∣st=qi,λ)=∑j=1NP(ot+1,ot+2,…,oT,st+1=qj∣st=qi,λ)=∑j=1NP(ot+1,ot+2,…,oT∣st+1=qj,st=qi,λ)P(st+1=qj∣st=qi,λ)\begin{aligned} \beta_{t}(i) &= P(o_{t+},o_{t+2},\dots,o_T\mid s_{t}=q_i,\lambda)\\ &= \sum_{j=1}^N P(o_{t+1},o_{t+2},\dots,o_T,s_{t+1}=q_j\mid s_{t}=q_i,\lambda) \\ &= \sum_{j=1}^N P(o_{t+1},o_{t+2},\dots,o_T\mid s_{t+1}=q_j,s_{t}=q_i,\lambda)P(s_{t+1}=q_j\mid s_t=q_i,\lambda) \\ \end{aligned} βt(i)=P(ot+,ot+2,…,oT∣st=qi,λ)=j=1∑NP(ot+1,ot+2,…,oT,st+1=qj∣st=qi,λ)=j=1∑NP(ot+1,ot+2,…,oT∣st+1=qj,st=qi,λ)P(st+1=qj∣st=qi,λ)
其中,根据 D-separation 可以将 {st}\{s_t\}{st} 视为集合 AAA,{st+1}\{s_{t+1}\}{st+1} 视为集合 BBB,{ot+1,ot+2,…,oT}\{o_{t+1},o_{t+2},\dots, o_T\}{ot+1,ot+2,…,oT} 视为集合 CCC。显然三者构成依赖关系中的顺序结构,存在性质 P(C∣B)=P(C∣A,B)P(C\mid B) = P(C\mid A,B)P(C∣B)=P(C∣A,B),即 A⊥C∣BA⊥C\mid BA⊥C∣B。因此,根据条件独立性和观测独立性假设可以对上式进一步变形
βt(i)=∑j=1NP(ot+1,ot+2,…,oT∣st+1=qj,λ)⋅aij=∑j=1NP(ot+1∣ot+2,ot+3,…,oT,st+1=qj,λ)P(ot+2,ot+3,…,oT∣st+1=qj,λ)⋅aij=∑j=1NP(ot+1∣st+1=qj,λ)P(ot+2,ot+3,…,oT∣st+1=qj,λ)⋅aij=∑j=1Nbj(ot+1)βt+1(j)aij(11)\begin{aligned} \beta_t(i) &= \sum_{j=1}^N P(o_{t+1},o_{t+2},\dots,o_T\mid s_{t+1}=q_j,\lambda)·a_{ij} \\ &=\sum_{j=1}^N P(o_{t+1}\mid o_{t+2},o_{t+3},\dots, o_T, s_{t+1}=q_j, \lambda) P(o_{t+2},o_{t+3}, \dots, o_T\mid s_{t+1}=q_j,\lambda) ·a_{ij} \\ &= \sum_{j=1}^N P(o_{t+1}\mid s_{t+1}=q_j, \lambda) P(o_{t+2},o_{t+3}, \dots, o_T\mid s_{t+1}=q_j,\lambda) ·a_{ij} \\ &= \sum_{j=1}^N b_j(o_{t+1})\beta_{t+1}(j)a_{ij} \tag{11} \end{aligned} βt(i)=j=1∑NP(ot+1,ot+2,…,oT∣st+1=qj,λ)⋅aij=j=1∑NP(ot+1∣ot+2,ot+3,…,oT,st+1=qj,λ)P(ot+2,ot+3,…,oT∣st+1=qj,λ)⋅aij=j=1∑NP(ot+1∣st+1=qj,λ)P(ot+2,ot+3,…,oT∣st+1=qj,λ)⋅aij=j=1∑Nbj(ot+1)βt+1(j)aij(11)
后向概率计算的动态过程如图 444 和 555 所示。
图 4 后向算法动态计算过程(详)
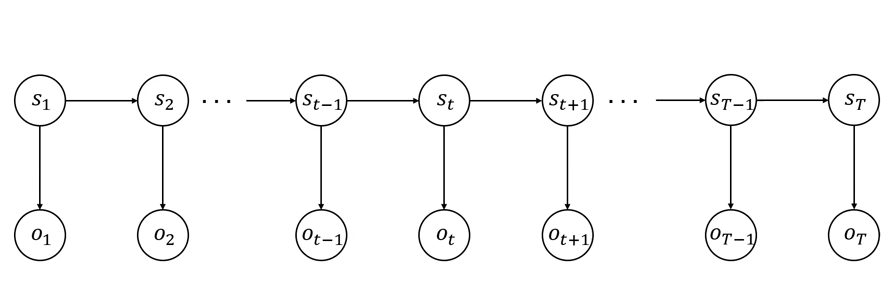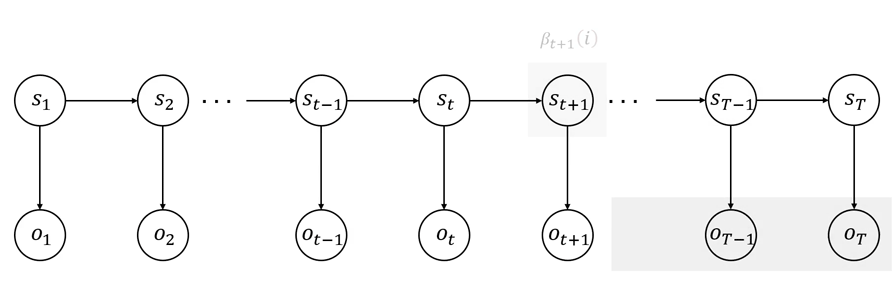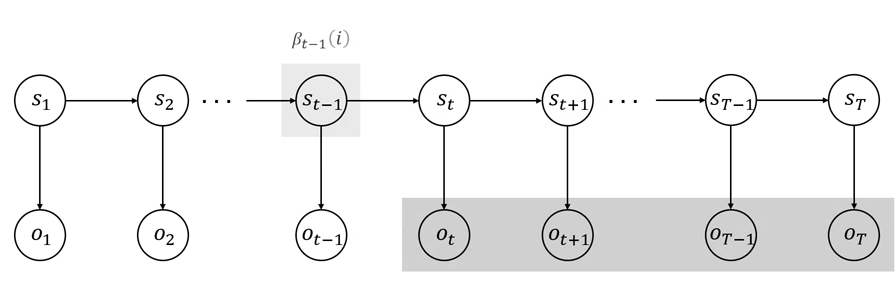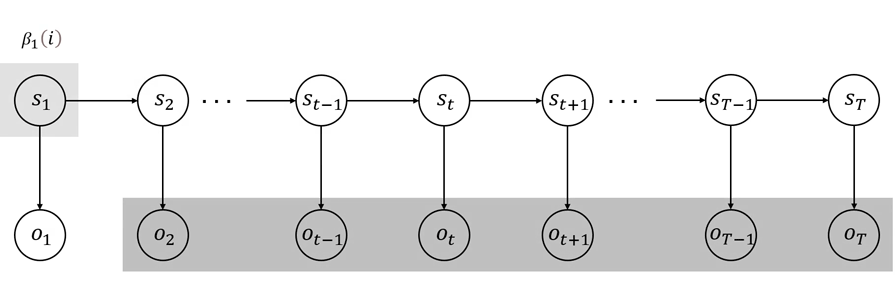
图 5 后向算法动态计算过程(简)
2.3.4. 前向、后向概率的相关计算
利用前向概率和后向概率可以得到一些下面会用到的概率。
-
P(O∣λ)P(O\mid \lambda)P(O∣λ) 的多种表达形式。
式 (6)(6)(6) 和式 (10)(10)(10) 展示了 P(O∣λ)P(O\mid \lambda)P(O∣λ) 为分别由前向概率和后向概率表示的形式,但是更为常用的其实是二者共同表示的形式。由前向概率和后向概率的定义可得
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ P(O\mid \lambd…
特别地,当 t=Tt=Tt=T 时式 (12)(12)(12) 变形为式 (6)(6)(6);当 t=Tt=Tt=T 时式 (12)(12)(12) 变形为式 (10)(10)(10)。另外,如果将式 (11)(11)(11) 代入到式 (12)(12)(12) 中得
P(O∣λ)=∑i=1N∑j=1Nαt(i)aijbj(ot+1)βt+1(j)(13)P(O\mid \lambda ) = \sum_{i=1}^N\sum_{j=1}^N \alpha_t(i) a_{ij} b_j(o_{t+1}) \beta_{t+1}(j) \tag{13} P(O∣λ)=i=1∑Nj=1∑Nαt(i)aijbj(ot+1)βt+1(j)(13)
由于 P(O∣λ)=∑i=1N∑j=1NP(O,st=qi,st+1=qj∣λ)P(O\mid \lambda) = \sum\limits_{i=1}^N\sum\limits_{j=1}^N P(O,s_t = q_i,s_{t+1}=q_j\mid \lambda)P(O∣λ)=i=1∑Nj=1∑NP(O,st=qi,st+1=qj∣λ),与式 (13)(13)(13) 相对应可得
P(O,st=qi,st+1=qj∣λ)=αt(i)aijbj(ot+1)βt+1(j)(14)P(O,s_t = q_i,s_{t+1}=q_j\mid \lambda) =\alpha_t(i) a_{ij} b_j(o_{t+1}) \beta_{t+1}(j)\tag{14} P(O,st=qi,st+1=qj∣λ)=αt(i)aijbj(ot+1)βt+1(j)(14) -
给定模型 λ\lambdaλ 和观测 OOO,在时刻 ttt 处于状态 qiq_iqi 的概率。
该概率记为
γt(i)=P(st=qi∣O,λ)(15)\gamma_t(i) = P(s_t = q_i \mid O,\lambda) \tag{15} γt(i)=P(st=qi∣O,λ)(15)
根据式 (12)(12)(12) 我们知道 P(O,st=qi∣λ)=αt(i)βt(i)P(O,s_t=q_i\mid \lambda)=\alpha_t(i)\beta_t(i)P(O,st=qi∣λ)=αt(i)βt(i) 和 P(O∣λ)=∑i=1Nαt(i)βt(i)P(O\mid \lambda) = \sum\limits_{i=1}^N \alpha_t(i)\beta_t(i)P(O∣λ)=i=1∑Nαt(i)βt(i),可得
γt(i)=P(st=qi∣O,λ)=P(O,st=qi∣λ)P(O∣λ)=αt(i)βt(i)∑i=1Nαt(i)βt(i)(16)\begin{aligned} \gamma_t(i) &= P(s_t = q_i\mid O,\lambda) \\ &=\frac{P(O,s_t=q_i\mid \lambda)}{P(O\mid \lambda)} \\ &= \frac{\alpha_t(i)\beta_t(i)}{\sum\limits_{i=1}^N \alpha_t(i)\beta_t(i)} \tag{16} \end{aligned} γt(i)=P(st=qi∣O,λ)=P(O∣λ)P(O,st=qi∣λ)=i=1∑Nαt(i)βt(i)αt(i)βt(i)(16) -
给定模型 λ\lambdaλ 和观测 OOO,在时刻 ttt 处于状态 qiq_iqi 且在时刻 t+1t+1t+1 处于状态 qjq_jqj 的概率。
该概率记为
ξt(i,j)=P(st=qi,st+1=qj∣O,λ)(17)\xi_t(i,j) = P(s_t=q_i,s_{t+1} =q_j\mid O,\lambda) \tag{17} ξt(i,j)=P(st=qi,st+1=qj∣O,λ)(17)
利用式 (13)(13)(13) 和式 (14)(14)(14) 对式 (17)(17)(17) 变形得
ξt(i,j)=P(O,st=qi,st+1=qj∣λ)P(O∣λ)=P(O,st=qi,st+1=qj∣λ)∑i=1N∑j=1NP(O,st=qi,st+1=qj∣λ)=αt(i)aijbj(ot+1)βt+1(j)∑i=1N∑j=1Nαt(i)aijbj(ot+1)βt+1(j)(18)\begin{aligned} \xi_t(i,j) &= \frac{P(O,s_t=q_i,s_{t+1} =q_j\mid\lambda)}{P(O\mid \lambda)} \\ &= \frac{P(O,s_t=q_i,s_{t+1} =q_j\mid\lambda)}{\sum\limits_{i=1}^N\sum\limits_{j=1}^N P(O,s_t=q_i,s_{t+1} =q_j\mid\lambda)} \\ &= \frac{\alpha_t(i) a_{ij} b_j(o_{t+1}) \beta_{t+1}(j)}{\sum\limits_{i=1}^N\sum\limits_{j=1}^N \alpha_t(i) a_{ij} b_j(o_{t+1}) \beta_{t+1}(j)}\tag{18} \end{aligned} ξt(i,j)=P(O∣λ)P(O,st=qi,st+1=qj∣λ)=i=1∑Nj=1∑NP(O,st=qi,st+1=qj∣λ)P(O,st=qi,st+1=qj∣λ)=i=1∑Nj=1∑Nαt(i)aijbj(ot+1)βt+1(j)αt(i)aijbj(ot+1)βt+1(j)(18)
观察式 (15)(15)(15) 和式 (17)(17)(17),很容易得出 γt(i)\gamma_t(i)γt(i) 与 ξt(i,j)\xi_t(i,j)ξt(i,j) 的关系
γt(i)=∑j=1Nξt(i,j)\gamma_t(i) = \sum_{j=1}^N \xi_t(i,j) γt(i)=j=1∑Nξt(i,j)
