树上操作【点分治】 - 原理 中心分解 【POJ No. 1741】 树上两点之间的路径数 Tree
树上操作【点分治】 - 原理 中心分解
分治法指将规模较大的问题分解为规模较小的子问题,解决各个子问题后合并得到原问题的答案。树上的分治算法分为点分治和边分治。
点分治经常用于带权树上的路径统计,本质上是一种带优化的暴力算法,并融入了容斥原理。对树上的路径,并不要求这棵树是有根树,无根树不影响统计结果。
分治法的核心是分解和治理。那么如何分?如何治?
数列上的分治法,通常从数列中间进行二等分,也就是说分解得到的两个子问题规模相当。若将n 个数分解为1、n -1,则分治法会退化为暴力穷举,那么对树怎么划分呢?
对树的划分要尽量均衡,不要出现一个子问题太大,另一个子问题太小的情况。也就是说,期望划分后每棵子树的节点数都不超过n /2。那么选择哪个节点作为划分点呢?可以选择树的重心。
树的重心指删除该节点后得到的最大子树的节点数最少。
定理: 删除重心后得到的所有子树,其节点数必然不超过n /2。
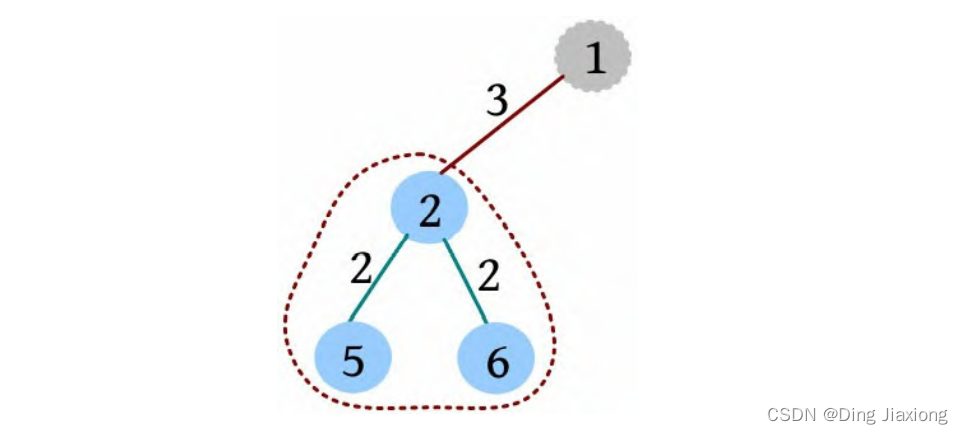
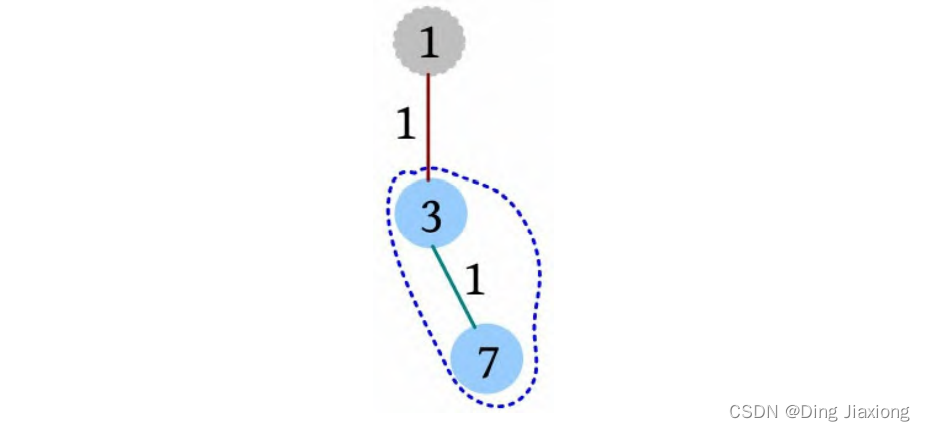
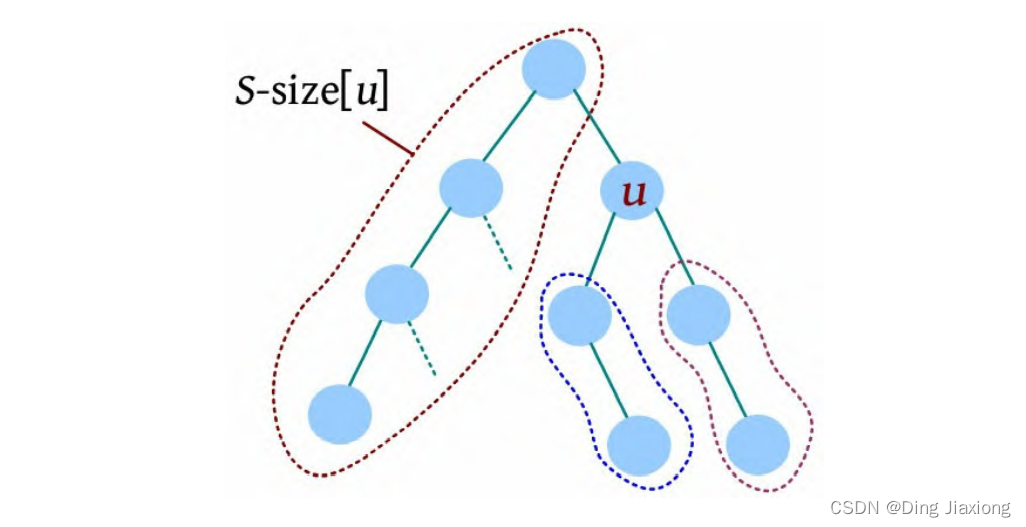
证明: 若s 为树的重心,则删除s 后得到的最大子树T 1 节点数最少。假设T 1 节点数m >n /2,则以s 为根的子树节点数 因此以树的重心作为划分点,每次划分后得到的子树大小减半,所以递归树的高度为O (logn )。 北大OJ 题目地址 【题意】 一棵有n 个节点的树,每条边都有一个长度(小于1001的正整数),dist(u , v )为节点u 和v 的最小距离。给定一个整数k ,对每对节点(u , v ),当且仅当dist(u , v )不超过k 时才叫作有效。计算给定的树中有多少对节点是有效的。 【输入输出】 输入: 输入包含几个测试用例。每个测试用例的第1行都包含两个整数n 、k (n ≤10000),下面的n -1行,每行都包含三个整数u 、v、l ,表示节点u 和v 之间有一条长度为l 的边。在最后一个测试用例后面跟着两个0。 输出: 对每个测试用例,都单行输出答案。 【样例】 【思路分析】 根据测试用例的输入数据,树形结构如下图所示。树中距离不超过4的有8对节点:1-2、1-3、1-4、1-5、2-3、3-4、3-5、4-5。 以树的重心root为划分点,则树上两点u 、v的路径分为两种:①经过root;②不经过root(两点均在root的一棵子树中),只需求解第1类路径,对第2类路径根据分治策略继续采用重心分解即可得到。 【算法设计】 ① 求树的重心root。 ② 从树的重心root出发,统计每个节点到root的距离。 ③ 对距离数组排序,以双指针扫描,统计以root为根的子树中满足条件的节点数。 ④ 对root的每一棵子树v 都减去重复统计的节点数。 ⑤ 从v 出发重复上述过程。 【举个栗子】 一棵树如下图所示,求解树上两点之间距离(路径长度)不超过4的路径数。 ① 求解树的重心,root=1。 ② 从树的重心root出发,统计每个节点到root的距离,得到距离数组dep[]。 ③ 对距离数组进行非递减排序,结果如下图所示。然后以双指针扫描,统计以root为根的子树中满足条件的节点数。 L =1,R =7,若dep[L ]+dep[R ]>4,则R --。 L =1,R =5,dep[L ]+dep[R ]<=4,则ans+=R -L =4,L ++。 为什么这么计算呢?因为序列从右向左递减,当dep[L ]+dep[R]≤4时,[L , R ]区间的其他节点与dep[L ]的和值必然也小于或等于4,该区间的节点个数为R -L ,累加即可。 L =2,R =5,若dep[L ]+dep[R ]≤4,则ans+=R -L =7,L ++。 L =3,R =5,若dep[L ]+dep[R ]>4,则R --。 L =3,R =4,若dep[L ]+dep[R ]≤4,则ans+=R -L =8,L ++,此时L =R ,算法停止。 也就是说,以1为根的树,满足条件的路径数有8个。在这些路径中,有些是合并路径,例如两条路径1-2和1-3,其路径长度之和为4,满足条件。这相当于将两条路径合并为2-1-3,路径长度为4。 第7条路径的合并是错误的。路径1-3和路径1-3-7的路径长度之和虽然小于或等于4,但是不可以作为合并路径,因为树中任意两个节点之间的路径都是不重复的。而路径1-3和路径1-3-7之间的路径有重复,所以这样的路径不可以作为合并路径。可以先统计该路径,然后在处理以3为根的子树时去重。 ④ 对root的每一棵子树v 都先去重,然后求以v 为根的子树的重心,重复上述过程。 ⑤ 去重。以2为根的子树没有重复统计的路径。 ⑥ 以2为根的子树的重心为2,该子树满足条件的路径有3条,ans+=3=11,这3条为2-5、2-6、2-5, 2-6(相当于一条合并路径5-2-6,路径长度为4)。 ⑦ 去重。以3为根的子树,该子树有一条重复统计的路径(1-3和1-3-7的合并路径)。减去重复路径,ans-1=10。 ⑧ 以3为根的子树的重心为3,该子树满足条件的路径有1条(3-7),路径长度为1,ans+1=11。 ⑨ 以4为根的子树的重心为4,该子树没有重复统计的路径,也没有满足条件的路径。 【算法实现】 ① 求树的重心。只需进行一次深度优先遍历,找到删除该节点后最大子树最小的节点。用f [u ]表示删除u 后最大子树的大小,size[u ]表示以u 为根的子树的节点数,S 表示整棵子树的节点数。先统计u 的所有子树中最大子树的节点数f [u ],然后与S -size[u ]比较,取最大值。 ② 统计每个节点到重心u 的距离。把dep[0]当作计数器使用,初始化为0,深度优先遍历,将每个节点到u 的距离d[]都存入dep数组中。 ③ 统计重心u 的子树中满足条件的个数。初始化d[u ]=dis且dep[0]=0(用于计数),将每个节点到u 的距离d[]都存入dep数组中;然后对dep数组排序,L =1,R =dep[0](dep数组末尾的下标),用sum累加满足条件的节点对个数。 ④ 对重心u 的所有子树都先去重,然后递归求解答案。对u 的每一棵子树v 都减去v 中重复统计的答案,然后从v 出发重复上述过程。 【算法分析】 因为每次都选择树的重心作为划分点,点分治至多递归O (logn )层,dep[]排序的时间复杂度为O (n logn ),因此总的时间复杂度为O(n log^2 n )。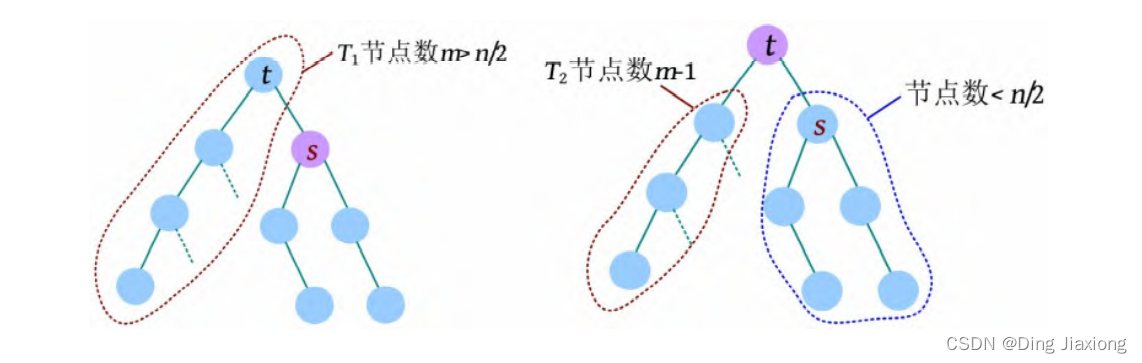
【POJ No. 1741】 树上两点之间的路径数 Tree

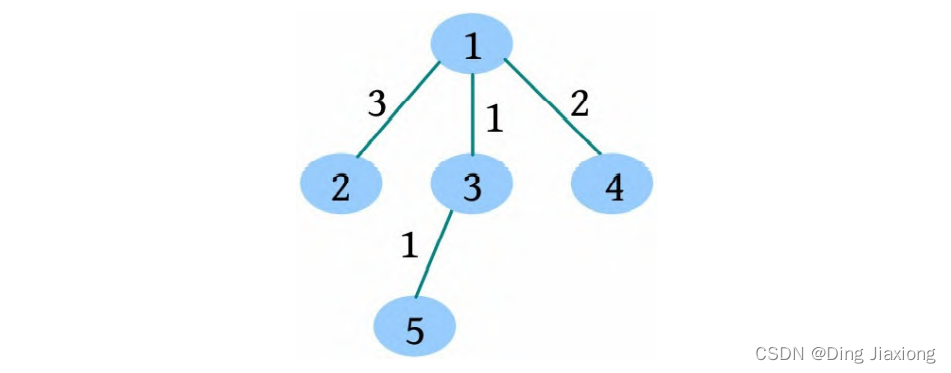
查询树中有多少对节点距离不超过k ,相当于查询树上两点之间距离不超过k 的路径有多少条。可采用点分治解决。当数据量很大时,树上两点之间的路径很多,采用暴力穷举的方法是不可行的,可以采用树上分治算法进行点分治。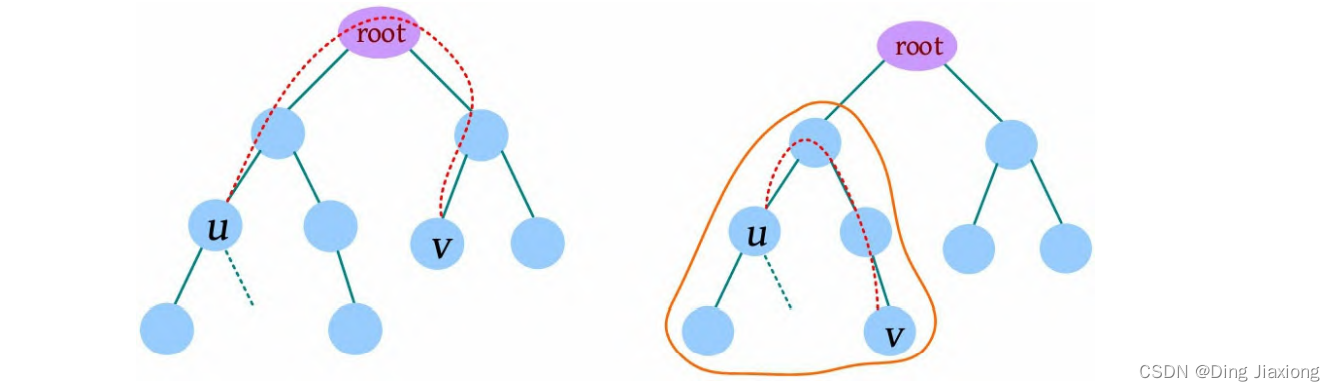
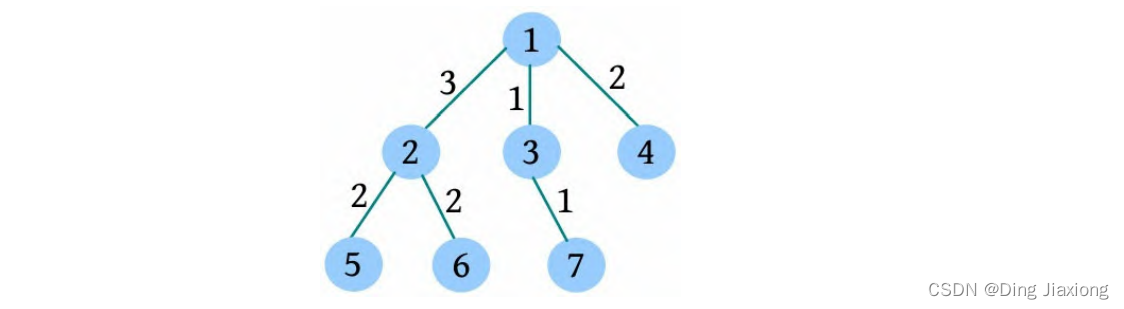
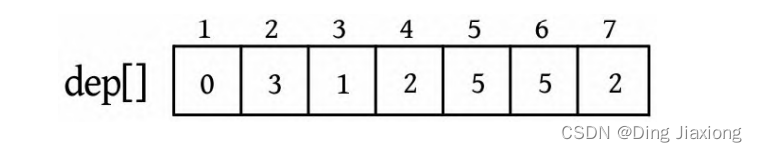

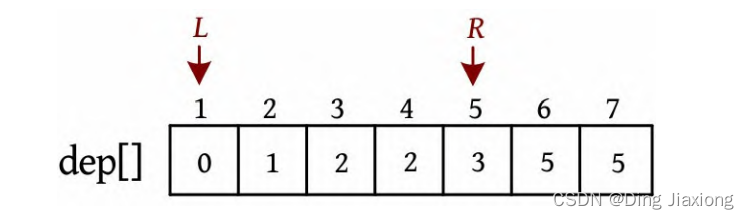
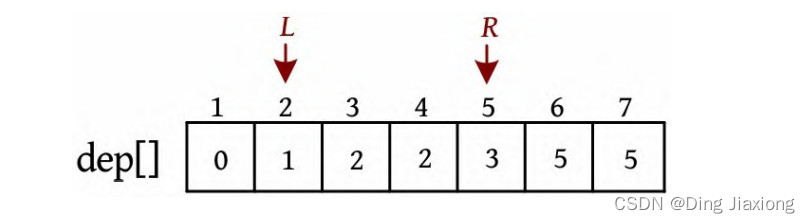
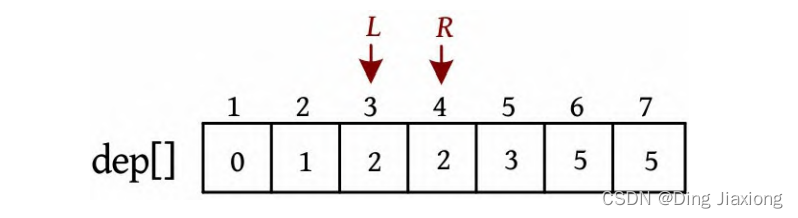
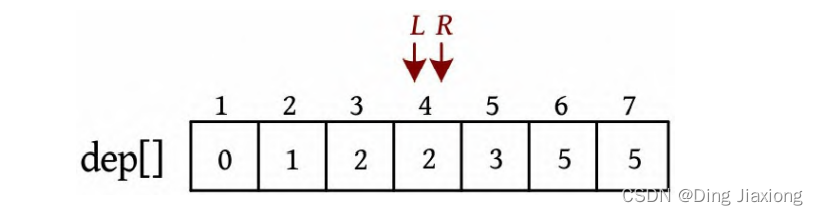
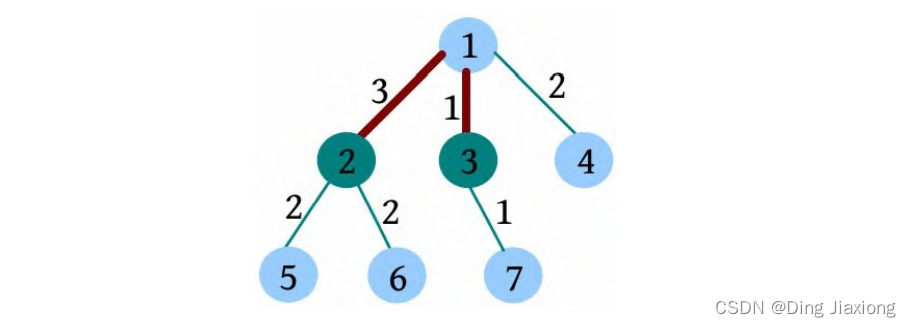
路径长度小于或等于4的8条路径如下表所示。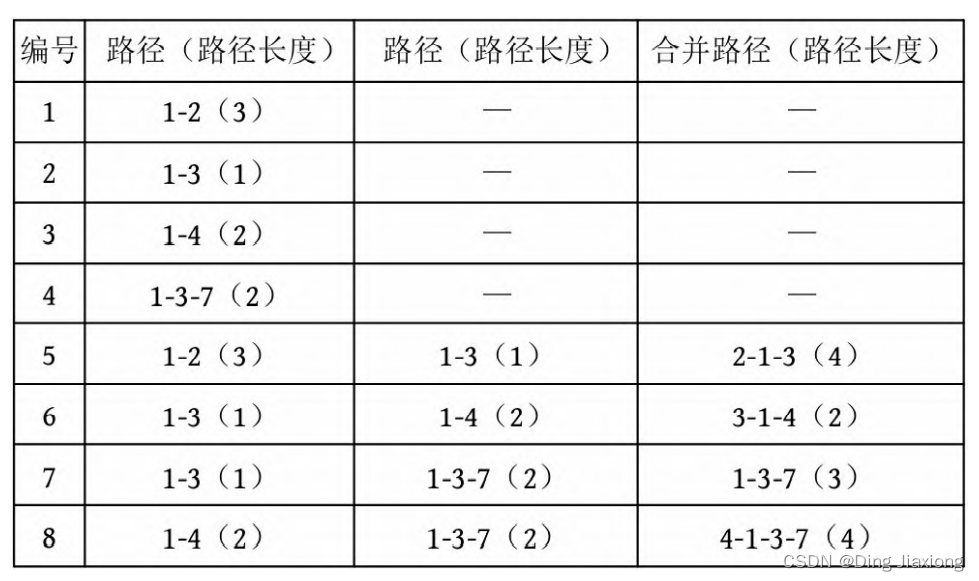
若f [u ]#include
