想要精通算法和SQL的成长之路 - 编辑距离

• 前言
• 一. 编辑距离
• • 1.1 定义动态规划数组
  • 1.2 定义动态规划方程
  • 1.3 定义数组的初始化
  • 1.4 最终答案

前言

想要精通算法和SQL的成长之路 - 系列导航

一. 编辑距离

原题链接

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数。你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

示例 1：

• 输入：word1 = “horse”, word2 = “ros”
• 输出：3
• 解释：horse -> rorse (将 ‘h’ 替换为 ‘r’)。rorse -> rose (删除 ‘r’)。rose -> ros (删除 ‘e’)

思路：遇到这种两个字符之间的序列、替换等问题。往往我们都是用动态规划。

1.1 定义动态规划数组

第一步：先来定义二维数组dp[i][j]：代表 word1 到第 i 位转化成 word2 第 j 位最少需要的步数。

1.2 定义动态规划方程

第二步：就是规定动态规划方程公式了。这里有两种情况：

• 第一种：word1[i] == word2[j] ，那么这种情况下就不需要插入/删除/替换。即dp[i][j] = dp[i-1][j-1] 。
• 第二种：word1[i] != word2[j]，那么这种情况又要单独分析。

我们来看上述第二种情况，当word1[i] != word2[j]的时候，根据题目提示，我们有三种选择：

1. word1当前位置插入： 相当于word1在i的位置转化成word2在j-1的位置所需要的最小步数再加1。即dp[i][j] = dp[i][j-1] + 1。（word1插入，相当于word2删除。反之同理）
2. word1当前位置删除：相当于word1在i-1的位置转化成word2在j的位置所需要的最小步数再加1。即dp[i][j] = dp[i-1][j] + 1。（word1删除，相当于word2插入。反之同理）
3. word1当前位置替换：那么元素的个数就不用改变。当于word1在i-1的位置转化成word2在j-1的位置所需要的最小步数再加1。即dp[i][j] = dp[i-1][j-1] + 1

但是总的来说，我们要求得最小步数 ，就应该对上述三种情况取最值。即最小值。

• dp[i][j] = min( dp[i-1][j] ,dp[i][j-1] ,dp[i-1][j-1] ) + 1

那么这部分代码就是：

for (int i = 1; i <= n1; i++) {for (int j = 1; j <= n2; j++) {if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;}}
}

最终结果返回：dp[word1.length()][word2.length()]。

1.3 定义数组的初始化

第三步：我们应该对dp数组进行初始化。这里引用leetcode上一位大佬的图：

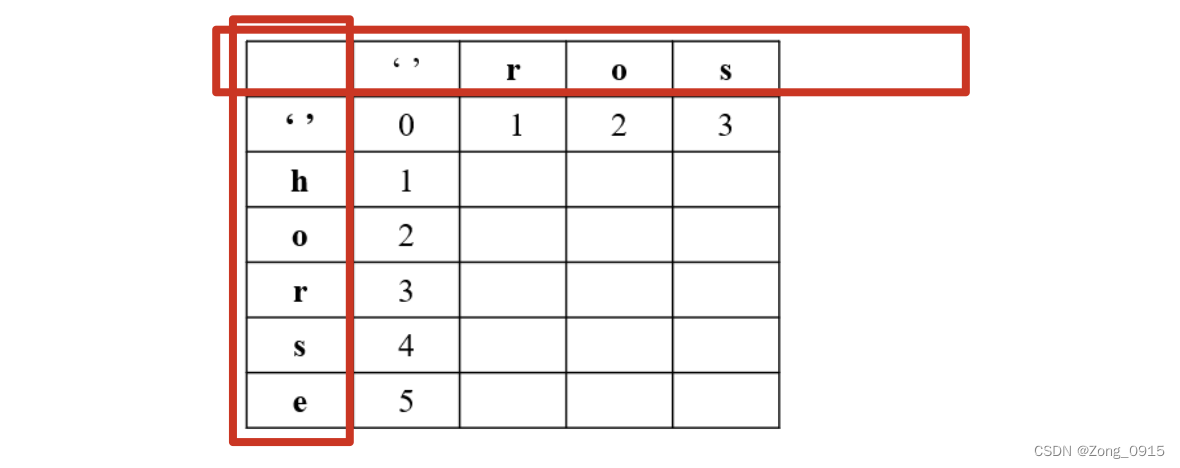
先说下红色框起来的部分：

1. 第一列代表word1每个位置的元素。第一行代表word2每个位置的元素。
2. 都包括空字符串。

再说下中间的数字部分（代表word1的第i位到word2的第j位转换所需的最少步数）：

1. 第一行：0,1,2,3。此时word1是空字符串，到word2的转换只能是插入操作。
2. 第一列：0,1,2,3,4,5。此时word2是空字符串，word1到word2的转换只能是删除操作。

那么初始化操作显而易见：

int n1 = word1.length(), n2 = word2.length();
int[][] dp = new int[n1 + 1][n2 + 1];
// 初始化,第一行
for (int j = 1; j <= n2; j++) {dp[0][j] = j;
}
// 初始化第一列
for (int i = 1; i <= n1; i++) {dp[i][0] = i;
}

1.4 最终答案

public int minDistance(String word1, String word2) {int n1 = word1.length(), n2 = word2.length();int[][] dp = new int[n1 + 1][n2 + 1];// 初始化,第一行for (int j = 1; j <= n2; j++) {dp[0][j] = j;}// 初始化第一列for (int i = 1; i <= n1; i++) {dp[i][0] = i;}for (int i = 1; i <= n1; i++) {for (int j = 1; j <= n2; j++) {if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;}}}return dp[n1][n2];
}