• 数学杂谈：圆上随机落点问题（一）
  • 1. 问题描述
  • 2. 问题解答
    • 1. 解法一：递推
    • 2. 解法二：受限制的均匀分布
    • 3. 数值模拟验证
  • 3. 讨论 & 扩展

1. 问题描述

这道题其实很早之前自己做过一遍，然后前阵子发现苏神也关于这道题进行了一些讨论，于是就把这道题重新拎出来做了一遍，这里也稍微整理一下这道题的解答。

问题：

• 在一个圆上随机抛nnn个点，求问这nnn个点均在同一个半圆上的概率是多少？

更进一步地，这道题还可以拓展为：

• 在一个圆上随机抛nnn个点，求问这nnn个点均可以被一个弧度为θ\thetaθ（θ≤π\theta \leq \piθ≤π）的弧形完全覆盖的概率是多少？

2. 问题解答

我们首先直接给出答案如下：

• nnn个点恰好落在弧度为θ\thetaθ的弧形中的概率密度函数为：

pn(θ)=n(n−1)2π(θ2π)n−2p_n(\theta) = \frac{n(n-1)}{2\pi}(\frac{\theta}{2\pi})^{n-2} pn​(θ)=2πn(n−1)​(2πθ​)n−2

• nnn个点能够被弧度为θ\thetaθ的弧形完全覆盖的概率为：

Pn(θ)=∫0θpn(φ)dφ=n(θ2π)n−1P_n(\theta) = \int_{0}^{\theta} p_n(\varphi)d\varphi = n(\frac{\theta}{2\pi})^{n-1} Pn​(θ)=∫0θ​pn​(φ)dφ=n(2πθ​)n−1

1. 解法一：递推

这一题我的一个直接的思路就是递推，显然，我们有：

p2(θ)=1πp_2(\theta) = \frac{1}{\pi}p2​(θ)=π1​

要使得nnn个点恰好构成一个弧度为θ\thetaθ的弧形，可以由以下两种情况构成：

1. 前n−1n-1n−1个点构成一个弧度为φ\varphiφ的弧形，且有φ≤θ\varphi \leq \thetaφ≤θ，此时第nnn个点需要与前n−1n-1n−1个点所构成的弧形的左边界或者右边界恰好构成θ\thetaθ角，且这个θ\thetaθ的弧形包含之前全部的n−1n-1n−1个点；
2. 前n−1n-1n−1个点已经构成一个弧度恰好为θ\thetaθ的弧形，此时第nnn个点只要落在弧形当中就可以。

因此，我们可以给出递推公式如下：

pn(θ)=12π[2⋅∫0θpn−1(φ)dφ+∫0θdφ⋅pn−1(θ)]p_n(\theta) = \frac{1}{2\pi} [2 \cdot \int_{0}^{\theta} p_{n-1}(\varphi) d\varphi + \int_{0}^{\theta}d\varphi \cdot p_{n-1}(\theta)] pn​(θ)=2π1​[2⋅∫0θ​pn−1​(φ)dφ+∫0θ​dφ⋅pn−1​(θ)]

综上，我们即可由数学归纳法解出fn(θ)f_n(\theta)fn​(θ)的通解表达式如下：

pn(θ)=n(n−1)2π(θ2π)n−2p_n(\theta) = \frac{n(n-1)}{2\pi}(\frac{\theta}{2\pi})^{n-2} pn​(θ)=2πn(n−1)​(2πθ​)n−2

积分即可得到：

Pn(θ)=∫0θpn(φ)dφ=n(θ2π)n−1P_n(\theta) = \int_{0}^{\theta} p_n(\varphi)d\varphi = n(\frac{\theta}{2\pi})^{n-1} Pn​(θ)=∫0θ​pn​(φ)dφ=n(2πθ​)n−1

2. 解法二：受限制的均匀分布

除了递推解法之外，事实上我们也可以将其视为一个受限制的均匀分布的概率求解问题。

我们以任意一个点作为起始点，然后顺时针旋转，显然圆上的nnn个点就会将整个圆切分为nnn个圆弧，然后我们要令这nnn个点可以恰好被一个弧度为θ\thetaθ的弧形覆盖，就是令这nnn个圆弧中最大的一个值恰好等于2π−θ2\pi-\theta2π−θ。

因此，问题也就可以转换为：

pn(θ)=Cn1⋅p(θi=2π−θ∣∑i=1nθi=2π)=Cn1⋅p(xi=1−θ2π∣∑i=1nxi=1)\begin{aligned} p_n(\theta) &= C_{n}^{1} \cdot p(\theta_i = 2\pi - \theta | \sum\limits_{i=1}^{n} \theta_i = 2\pi) \\ &= C_{n}^{1} \cdot p(x_i = 1 - \frac{\theta}{2\pi} | \sum\limits_{i=1}^{n} x_i = 1) \end{aligned} pn​(θ)​=Cn1​⋅p(θi​=2π−θ∣i=1∑n​θi​=2π)=Cn1​⋅p(xi​=1−2πθ​∣i=1∑n​xi​=1)​

而关于这个受限制的概率问题，我们在之前的博客文章【数学杂谈：限制条件下的均匀分布考察】当中，事实上已经对这个问题有过了考察，我们直接给出答案如下：

p(xi=1−θ2π∣∑i=1nxi=1)=(n−1)(θ2π)n−2p(x_i = 1 - \frac{\theta}{2\pi} | \sum\limits_{i=1}^{n} x_i = 1) = (n-1) (\frac{\theta}{2\pi})^{n-2} p(xi​=1−2πθ​∣i=1∑n​xi​=1)=(n−1)(2πθ​)n−2

又因为x=θ2πx = \frac{\theta}{2\pi}x=2πθ​，因此，我们将其作变量代换之后即有：

pn(θ)=n(n−1)2π(θ2π)n−2p_n(\theta) = \frac{n(n-1)}{2\pi}(\frac{\theta}{2\pi})^{n-2} pn​(θ)=2πn(n−1)​(2πθ​)n−2

而积分即可计算得到：

Pn(θ)=∫0θpn(φ)dφ=n(θ2π)n−1P_n(\theta) = \int_{0}^{\theta} p_n(\varphi)d\varphi = n(\frac{\theta}{2\pi})^{n-1} Pn​(θ)=∫0θ​pn​(φ)dφ=n(2πθ​)n−1

与上述递推解法得到的结果是完全一致的。

3. 数值模拟验证

最后，我们用monte-carlo模拟来验证一下我们上述结论的可靠性。

给出monte-carlo模拟的代码实现如下：

import math
from random import random
from matplotlib import pyplot as pltdef simulate(theta, n, N=100000):def get_radian(plist):plist = sorted(plist)deltas = [plist[(i+1) % n] - plist[i] + 2 * math.pi for i in range(n)]deltas = [x if x < 2 * math.pi else x - 2 * math.pi for x in deltas]return math.pi * 2 - max(deltas)cnt = 0for _ in range(N):plist = [random() * 2 * math.pi for _ in range(n)]radian = get_radian(plist)if radian <= theta:cnt += 1return cnt / Ndef plot_simulate(n, delta=10, max_degree=180, N=10000):degrees = list(range(0, max_degree, delta))degrees.append(max_degree)x = [deg / 180 * math.pi for deg in degrees]y = [simulate(phi, n) for phi in x]z = [n * (deg/360)**(n-1) for deg in degrees]plt.figure(figsize=(15, 7))plt.scatter(degrees, y, marker="x", label="monte-carlo")plt.plot(degrees, z, color="orange", label=r"$P_n ( \theta )$")plt.legend()plt.grid()plt.show()returnplot_simulate(5, delta=5, max_degree=180, N=10000)

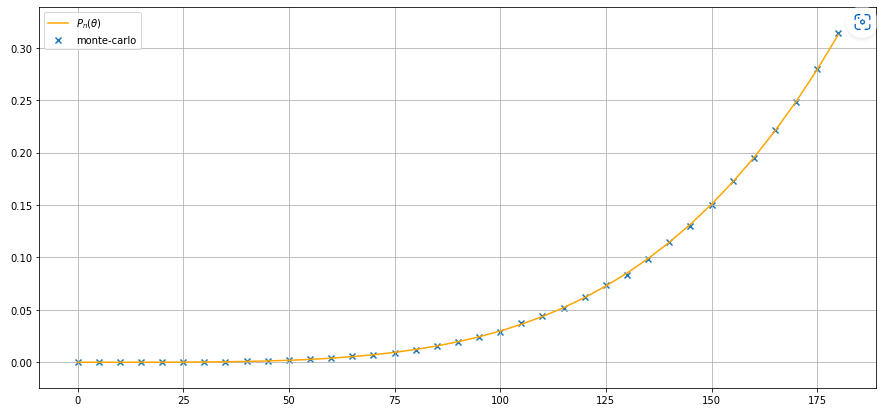
可以看到：

• 当θ≤180°\theta \leq 180\degreeθ≤180°时，曲线与拟合结果符合的非常完美。

3. 讨论 & 扩展

这里，其实大部分读者也都注意到了，这里我们反复地在强调，θ≤180°\theta \leq 180\degreeθ≤180°。

但是，对于圆上的随机nnn个点，事实上要能够覆盖住这nnn个点，所需的最小弧形的弧度是可以大于180°180\degree180°的。更确切地，简单计算可以发现，这个最小弧度的最大值可以一直取到θ=n−1nπ\theta = \frac{n-1}{n}\piθ=nn−1​π。

那么，对于θ≥180°\theta \geq 180\degreeθ≥180°的情况时，上述推论是否还成立呢？

答案是不成立，我们直接给出上述曲线拟合结果即可：

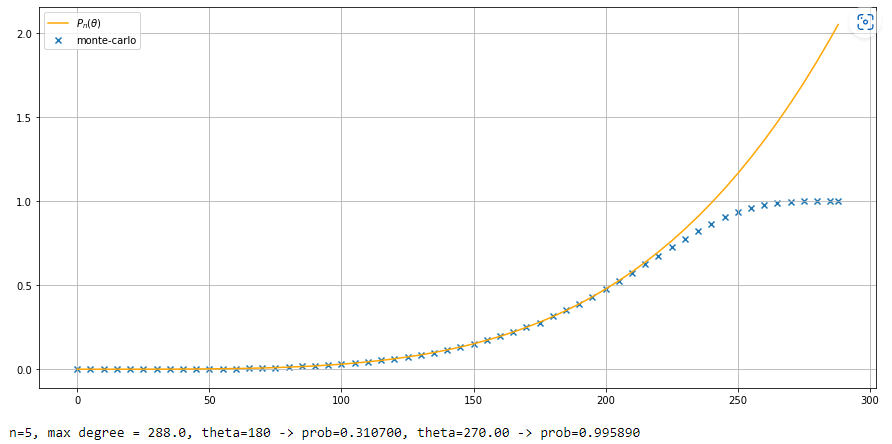
可以看到：

• 显然，当弧度超过180°180\degree180°时，上述拟合公式就不再成立，且两者差距会越来越大。

我们分别说明一下上述两种方法为何在180°180\degree180°以上的情况下会失效：

1. 递推方法
   • 递推方法的第一个部分存在一个隐藏条件，就是当前n−1n-1n−1个点所构成的角度为ϕ\phiϕ时，新加入的第nnn个点所构成的新的弧形所需要覆盖的最小角度为θ\thetaθ，但是这个假设在θ≥180°\theta \geq 180\degreeθ≥180°时不一定成立的，因为有可能另一侧覆盖的角度反而小于θ\thetaθ。
2. 受限均匀分布方法
   • 同样的，首先的均匀分布其实要求的条件是，存在某一个角度不小于2π−θ2\pi-\theta2π−θ，这个条件在θ≤180°\theta \leq 180\degreeθ≤180°的情况下是唯一的，因为至多只能有一个角度大于这个值，因此我们可以直接乘以系数Cn1C_{n}^{1}Cn1​，但是当θ≥180°\theta \geq 180\degreeθ≥180°时，这个条件就不一定满足了，因此推导的结果自然也就不再满足了。

综上，我们就说明白了为啥上述结论在θ≥180°\theta \geq 180\degreeθ≥180°时不成立。

不过真要求当θ≥180°\theta \geq 180 \degreeθ≥180°的情况下时的解的话，事实上也可以仿照上述受限制下的分布给出Pn(θ)P_n(\theta)Pn​(θ)的概率如下：

Pn(θ)=1−∫02π−θdθ1∫0min(2π−θ,2π−θ1)dθ2...∫0min(2π−θ,2π−∑i=1n−2θi)dθn−1∫0min(2π−θ,2π−∑i=1n−1θi)δ(θn=2π−∑i=1n−1θi)dθn∫02πdθ1∫02π−θ1dθ2...∫02π−∑i=1n−2θidθn−1∫02π−∑i=1n−1θiδ(θn=2π−∑i=1n−1θi)dθnP_n(\theta) = 1 - \frac{\int_{0}^{2\pi-\theta}d\theta_1 \int_{0}^{\mathop{min}(2\pi-\theta, 2\pi-\theta_1)}d\theta_2 ... \int_{0}^{\mathop{min}(2\pi-\theta, 2\pi-\sum\limits_{i=1}^{n-2}\theta_i)}d\theta_{n-1} \int_{0}^{\mathop{min}(2\pi-\theta, 2\pi-\sum\limits_{i=1}^{n-1}\theta_i)}\delta(\theta_n = 2\pi-\sum\limits_{i=1}^{n-1}\theta_i) d\theta_{n}}{\int_{0}^{2\pi}d\theta_1\int_{0}^{2\pi-\theta_1}d\theta_2 ... \int_{0}^{2\pi-\sum\limits_{i=1}^{n-2}\theta_i}d\theta_{n-1} \int_{0}^{2\pi-\sum\limits_{i=1}^{n-1}\theta_i} \delta(\theta_n = 2\pi-\sum\limits_{i=1}^{n-1}\theta_i) d\theta_{n}} Pn​(θ)=1−∫02π​dθ1​∫02π−θ1​​dθ2​...∫02π−i=1∑n−2​θi​​dθn−1​∫02π−i=1∑n−1​θi​​δ(θn​=2π−i=1∑n−1​θi​)dθn​∫02π−θ​dθ1​∫0min(2π−θ,2π−θ1​)​dθ2​...∫0min(2π−θ,2π−i=1∑n−2​θi​)​dθn−1​∫0min(2π−θ,2π−i=1∑n−1​θi​)​δ(θn​=2π−i=1∑n−1​θi​)dθn​​

即在∑i=1nθi=2π\sum\limits_{i=1}^{n}\theta_i=2\pii=1∑n​θi​=2π的情况下，至少存在一个θi\theta_iθi​使得θi≥2π−θ\theta_i \geq 2\pi-\thetaθi​≥2π−θ时的概率。

事实上，考虑到δ\deltaδ函数事实上已经内隐的限制条件内容，我们可以简化上式为：

Pn(θ)=1−∫02π−θdθ1∫02π−θdθ2...∫02π−θdθn−1∫02π−θδ(θn=2π−∑i=1n−1θi)dθn∫02πdθ1∫02π−θ1dθ2...∫02π−∑i=1n−2θidθn−1∫02π−∑i=1n−1θiδ(θn=2π−∑i=1n−1θi)dθnP_n(\theta) = 1 - \frac{\int_{0}^{2\pi-\theta}d\theta_1 \int_{0}^{2\pi-\theta}d\theta_2 ... \int_{0}^{2\pi-\theta}d\theta_{n-1} \int_{0}^{2\pi-\theta}\delta(\theta_n = 2\pi-\sum\limits_{i=1}^{n-1}\theta_i) d\theta_{n}}{\int_{0}^{2\pi}d\theta_1\int_{0}^{2\pi-\theta_1}d\theta_2 ... \int_{0}^{2\pi-\sum\limits_{i=1}^{n-2}\theta_i}d\theta_{n-1} \int_{0}^{2\pi-\sum\limits_{i=1}^{n-1}\theta_i} \delta(\theta_n = 2\pi-\sum\limits_{i=1}^{n-1}\theta_i) d\theta_{n}} Pn​(θ)=1−∫02π​dθ1​∫02π−θ1​​dθ2​...∫02π−i=1∑n−2​θi​​dθn−1​∫02π−i=1∑n−1​θi​​δ(θn​=2π−i=1∑n−1​θi​)dθn​∫02π−θ​dθ1​∫02π−θ​dθ2​...∫02π−θ​dθn−1​∫02π−θ​δ(θn​=2π−i=1∑n−1​θi​)dθn​​

但是，不幸的是，即便有了上述一般的表达式，这依然不是一个可以快速求解的表达式，甚至不确定这个表达式能否真的去解析求解。

不过问了我同学之后，他倒是修正了迭代的方法，给出了一个非常完美的回答，不过这里我就先不做展开了，后面我会花点时间把他的解答好好整理一下之后然后再发出来吧。