无目录

如图所示电路，输入端电压eie_iei​，输出端电压eoe_oeo​，求二者之间关系。

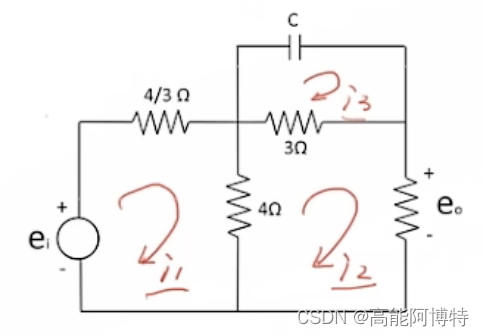
对其中元件进行标号，并将电流环路标号，指出各元件的压降方向：

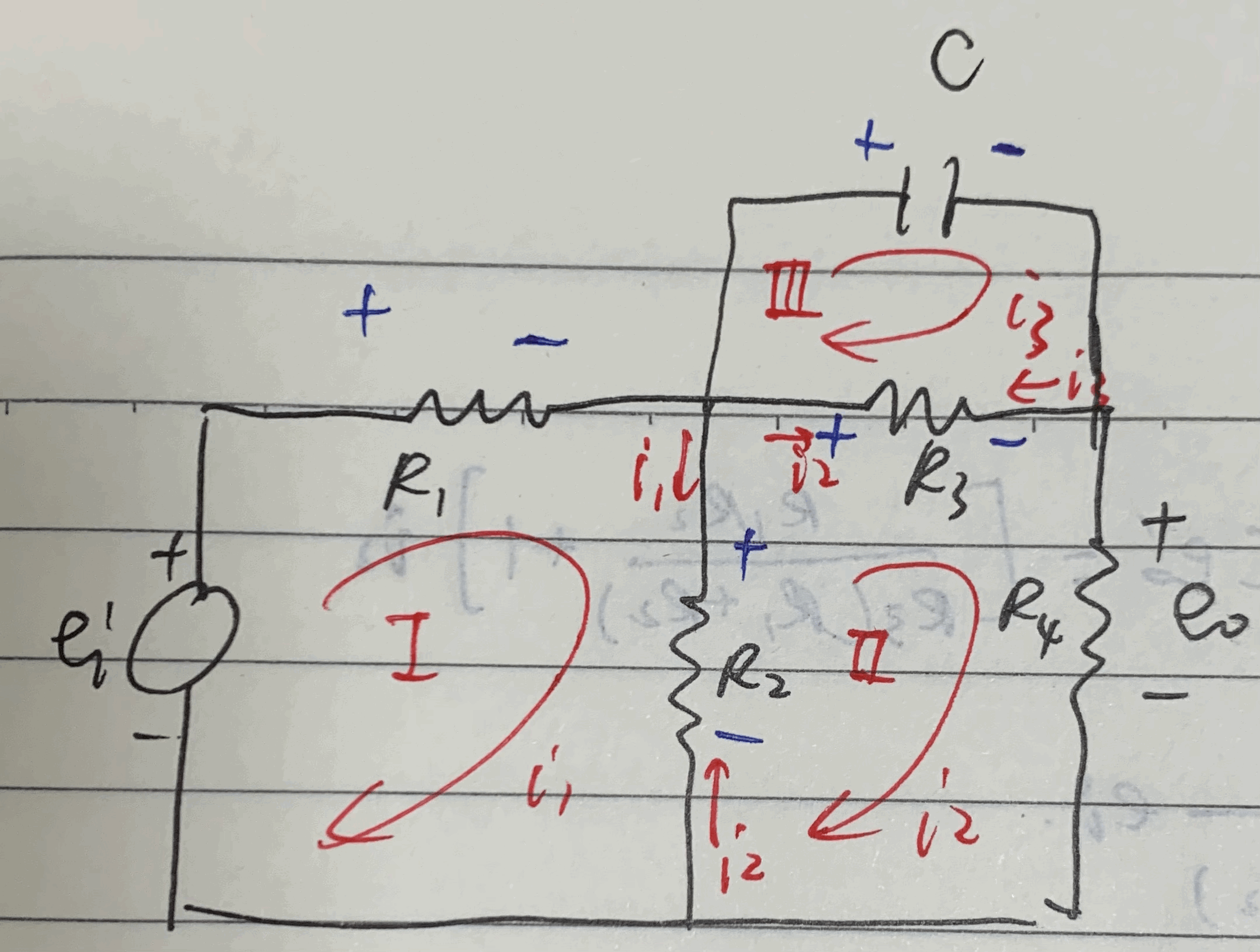
v值得注意的是：
1）电阻R2R_2R2​同时占据环路I与环路II，按照图中规定的压降方向，其上电流应该为i1−i2i_1-i_2i1​−i2​。
2）同理，电阻R3R_3R3​上的电流应该为i2−i3i_2-i_3i2​−i3​。

对3条环路，列出3个KVL方程：
环路1：
i1R1+(i1−i2)R2=ei(1)i_1 R_1 + \left( i_1 - i_2 \right) R_2 = e_i \tag{1} i1​R1​+(i1​−i2​)R2​=ei​(1)(i2−i3)R3+eo=(i1−i2)R2(2)\left( i_2 - i_3 \right) R_3 + e_o = \left( i_1 - i_2 \right) R_2 \tag{2} (i2​−i3​)R3​+eo​=(i1​−i2​)R2​(2)1C∫0ti3dt=(i2−i3)R3(3)\frac{1}{C} \int_0^t {i_3} dt = \left( i_2 - i_3 \right) R_3 \tag{3} C1​∫0t​i3​dt=(i2​−i3​)R3​(3)同时输出端还有
eo=i2R4(4)e_o = i_2 R_4 \tag{4} eo​=i2​R4​(4)将(1)(2)(3)联立有
1C∫0ti3dt+i2R4=ei−i1R1(5)\frac{1}{C} \int_0^t {i_3} dt + i_2 R_4 = e_i - i_1 R_1 \tag{5} C1​∫0t​i3​dt+i2​R4​=ei​−i1​R1​(5)同时，由(1)可以推出：
i1=eiR1+R2+R2R1+R2i2(6)i_1 = \frac{e_i}{R_1 + R_2} + \frac{R_2}{R_1 + R_2} i_2 \tag{6} i1​=R1​+R2​ei​​+R1​+R2​R2​​i2​(6)将i1i_1i1​表达式代入(4)：
1C∫0ti3dt=R2R1+R2ei−R1R2R1+R2i2−eo(7)\frac{1}{C} \int_0^t i_3 dt = \frac{R_2}{R_1 + R_2} e_i - \frac{R_1 R_2}{R_1 + R_2} i_2 - e_o \tag{7} C1​∫0t​i3​dt=R1​+R2​R2​​ei​−R1​+R2​R1​R2​​i2​−eo​(7)对其求导
1Ci3=R2R1+R2deidt−R1R2R1+R2di2dt−deodt(8)\frac{1}{C} i_3 = \frac{R_2}{R_1 + R_2} \frac{de_i}{dt} - \frac{R_1 R_2}{R_1 + R_2} \frac{di_2}{dt} - \frac{de_o}{dt} \tag{8} C1​i3​=R1​+R2​R2​​dtdei​​−R1​+R2​R1​R2​​dtdi2​​−dtdeo​​(8)另一方面，由(3)又有
R2R1+R2ei−R1R2R1+R2i2−eo=(i2−i3)R3⟹\frac{R_2}{R_1 + R_2} e_i - \frac{R_1 R_2}{R_1 + R_2} i_2 - e_o = \left( i_2 - i_3 \right) R_3 \Longrightarrow R1​+R2​R2​​ei​−R1​+R2​R1​R2​​i2​−eo​=(i2​−i3​)R3​⟹i3R3=(R1R2R1+R2+R3)i2+eo−R2R1+R2ei⟹i_3 R_3 = \left( \frac{R_1 R_2}{R_1 + R_2} + R_3 \right) i_2 + e_o - \frac{R_2}{R_1 + R_2} e_i \Longrightarrow i3​R3​=(R1​+R2​R1​R2​​+R3​)i2​+eo​−R1​+R2​R2​​ei​⟹i3=[R1R2R3(R1+R2)+1]i2+1R3eo−R2R3(R1+R2)ei(9)i_3 = \left[ \frac{R_1 R_2}{R_3 \left( R_1 + R_2 \right)} + 1 \right] i_2 + \frac{1}{R_3} e_o - \frac{R_2}{R_3 \left( R_1 + R_2 \right)} e_i \tag{9} i3​=[R3​(R1​+R2​)R1​R2​​+1]i2​+R3​1​eo​−R3​(R1​+R2​)R2​​ei​(9)将(8)(9)联立
CR2R1+R2deidt−CR1R2R1+R2di2dt−Cdeodt=[R1R2R3(R1+R2)+1]i2+1R3eo−R2R3(R1+R2)ei\frac{C R_2}{R_1 + R_2} \frac{de_i}{dt} - \frac{C R_1 R_2}{R_1 + R_2} \frac{di_2}{dt} - C \frac{de_o}{dt} = \left[ \frac{R_1 R_2}{R_3 \left( R_1 + R_2 \right)} +1 \right] i_2 + \frac{1}{R_3} e_o - \frac{R_2}{R_3 \left( R_1 + R_2 \right)} e_i R1​+R2​CR2​​dtdei​​−R1​+R2​CR1​R2​​dtdi2​​−Cdtdeo​​=[R3​(R1​+R2​)R1​R2​​+1]i2​+R3​1​eo​−R3​(R1​+R2​)R2​​ei​又因为eo=i2R4e_o = i_2 R_4eo​=i2​R4​，因此上式化为
CR2R4R1+R2deidt+R2R4R3(R1+R2)ei=C(R1R2R1+R2+R4)deodt+[R1R2R3(R1+R2)+R4R3+1]eo(10)\frac{C R_2 R_4}{R_1 + R_2} \frac{de_i}{dt} + \frac{R_2 R_4}{R_3 \left( R_1 + R_2 \right)} e_i = C \left( \frac{R_1 R_2}{R_1 + R_2} + R_4 \right) \frac{de_o}{dt} + \left[ \frac{R_1 R_2}{R_3 \left( R_1 + R_2 \right)} + \frac{R_4}{R_3} +1 \right] e_o \tag{10} R1​+R2​CR2​R4​​dtdei​​+R3​(R1​+R2​)R2​R4​​ei​=C(R1​+R2​R1​R2​​+R4​)dtdeo​​+[R3​(R1​+R2​)R1​R2​​+R3​R4​​+1]eo​(10)
(10)式即为最终得到的eie_iei​与eoe_oeo​关系式。

带入值：R1=43Ω,R2=4Ω,R3=3Ω,R4=2ΩR_1 = \frac{4}{3} \Omega, R_2 = 4 \Omega, R_3 = 3 \Omega, R_4 = 2 \OmegaR1​=34​Ω,R2​=4Ω,R3​=3Ω,R4​=2Ω有
32Cdeodt+eo=34Cdeidt+14ei.\frac{3}{2} C \frac{de_o}{dt} + e_o = \frac{3}{4} C \frac{de_i}{dt} + \frac{1}{4} e_i. 23​Cdtdeo​​+eo​=43​Cdtdei​​+41​ei​.

关键点难点解析
注意跨环路的电阻R2R_2R2​与R3R_3R3​上的电流的表达式。