​🌠 作者：@阿亮joy.
🎆专栏：《吃透西嘎嘎》
🎇 座右铭：每个优秀的人都有一段沉默的时光，那段时光是付出了很多努力却得不到结果的日子，我们把它叫做扎根

目录

• • 👉二叉树的前序遍历👈
  • 👉二叉树的中序遍历👈
  • 👉二叉树的后序遍历👈
  • 👉总结👈

👉二叉树的前序遍历👈

前序遍历的顺序是根、左子树、右子树。那么首先访问的一定是左路节点，再来访问左路节点的右子树。而访问左路节点的右子树又可以看成一个子问题，那么就能像递归访问整棵树了。

思路：

• 想定义一个栈st、一个vector v和一个TreeNode* cur，cur初始化为root。
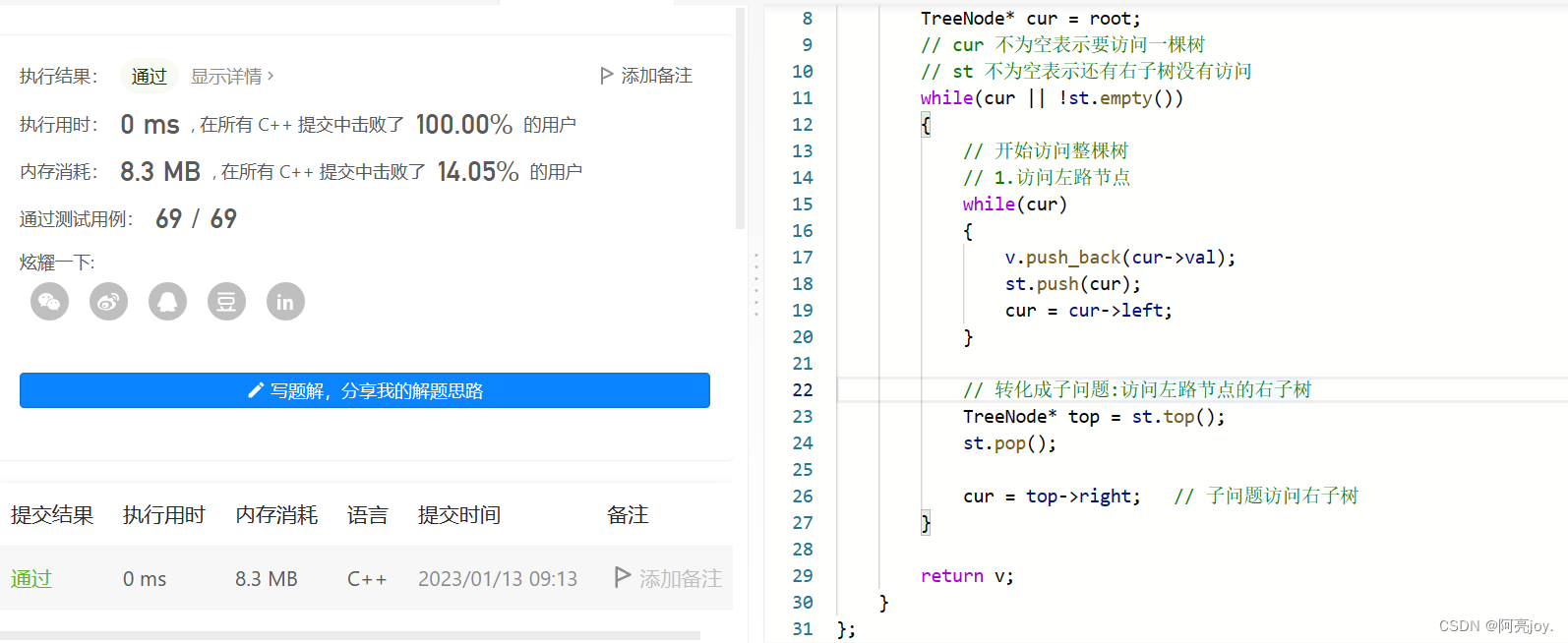
• 当cur不为空或者st不为空时，while继续。while循环里做一下操作：左路节点入栈的同时尾插到v中，那么左路节点就访问完了。然后取出栈顶节点top，将cur置为top->right，这样就可以转化成子问题去访问左路节点的右子树了。
• cur不为空表示要访问一棵树，st不为空表示还有左路节点的右子树没有访问。两个同时为空时，while循环结束，得到正确的前序遍历。
• 注：一个节点出栈意味着这个节点及其左子树已经访问完了，还剩右子树没有访问。

class Solution 
{
public:vector preorderTraversal(TreeNode* root) {stack st;vector v;TreeNode* cur = root;// cur 不为空表示要访问一棵树// st 不为空表示还有右子树没有访问while(cur || !st.empty()){// 开始访问整棵树// 1.访问左路节点while(cur){v.push_back(cur->val);st.push(cur);cur = cur->left;}// 转化成子问题:访问左路节点的右子树TreeNode* top = st.top();st.pop();cur = top->right;   // 子问题访问右子树}return v;}
};

👉二叉树的中序遍历👈

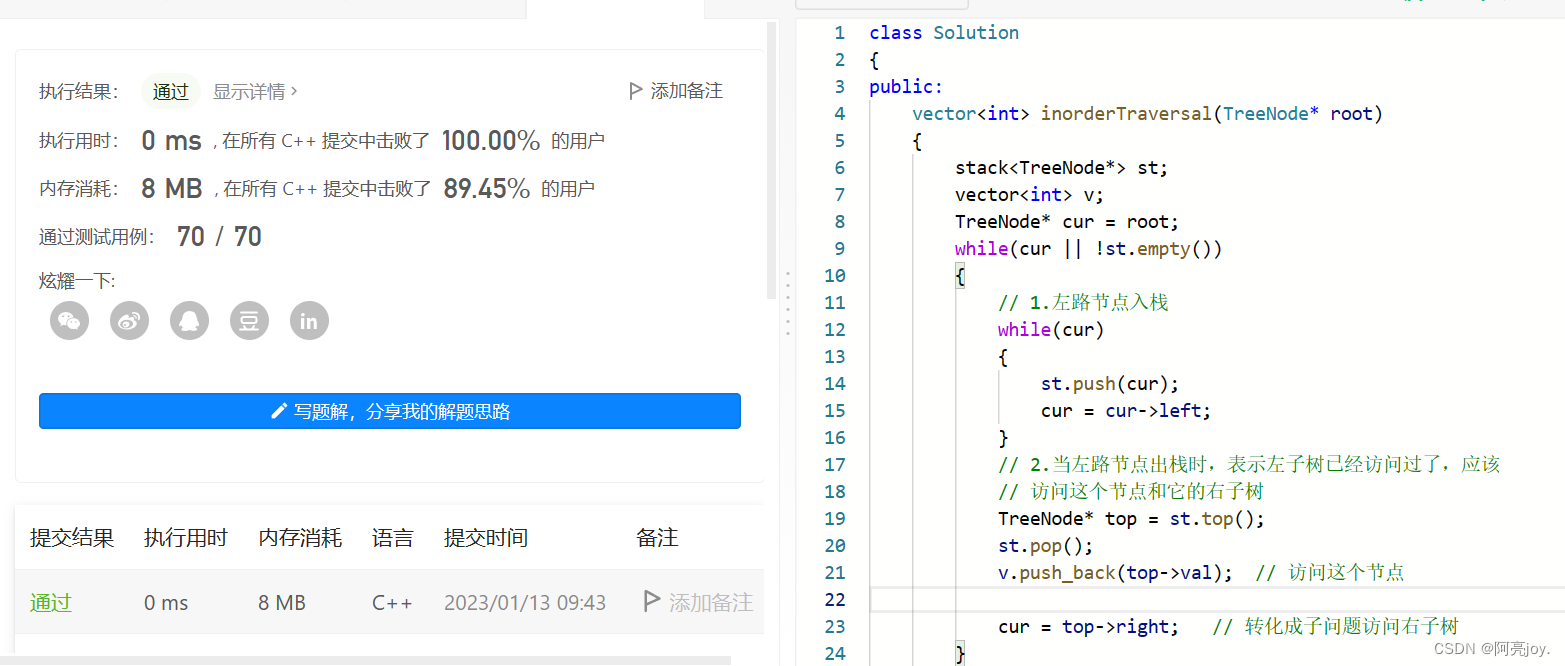
中序遍历的顺序是左子树、根、右子树。首先，和中序遍历一样的是左路节点入栈，入栈的同时不能访问该节点，即不能将节点的值尾插到vector中。当左路节点出栈时，表示当前节点的左子树已经访问完了，开始访问当前节点及其右子树。

class Solution 
{
public:vector inorderTraversal(TreeNode* root) {stack st;vector v;TreeNode* cur = root;while(cur || !st.empty()){// 1.左路节点入栈while(cur){st.push(cur);cur = cur->left;}// 2.当左路节点出栈时，表示左子树已经访问过了，应该// 访问这个节点和它的右子树TreeNode* top = st.top();st.pop();v.push_back(top->val);  // 访问这个节点cur = top->right;   // 转化成子问题访问右子树}return v;}
};

👉二叉树的后序遍历👈

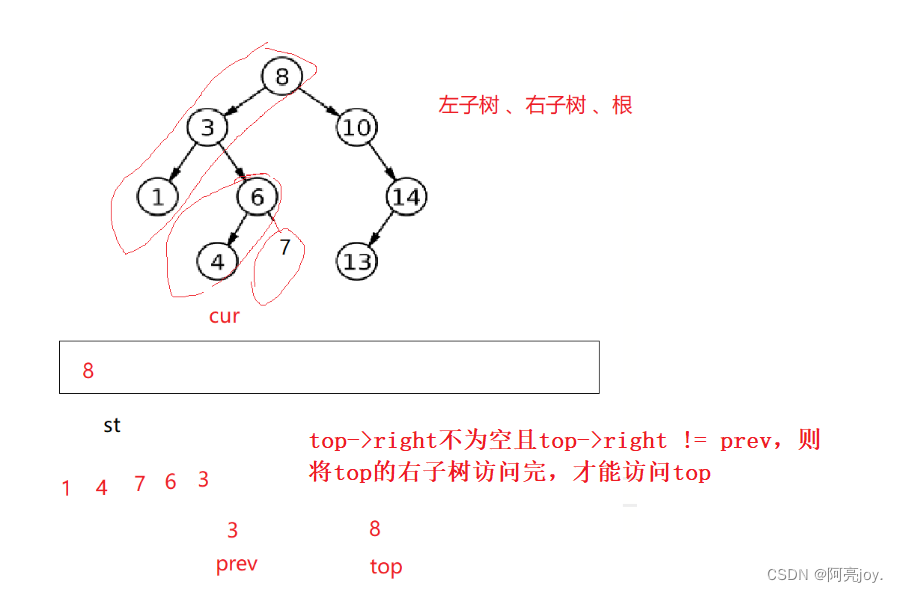
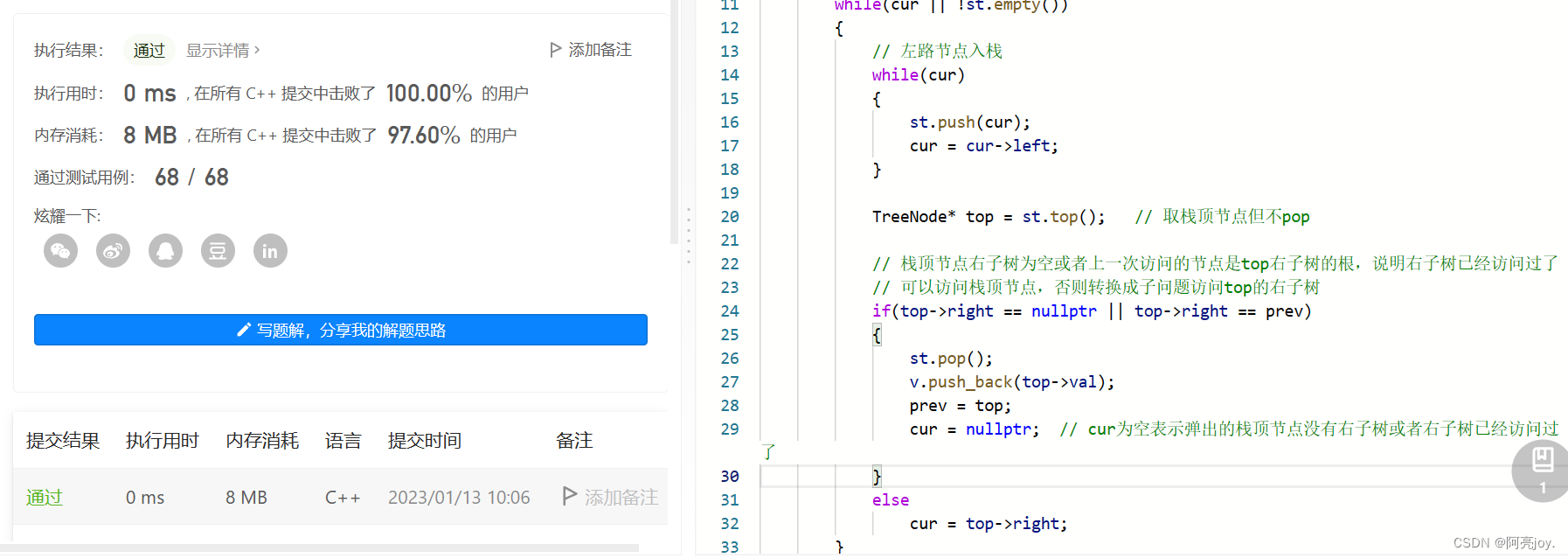
后序遍历的顺序是左子树、右子树、根，需要将左子树和右子树访问完了，才能访问根。如果栈顶节点为空或者栈顶节点的右子树已经访问过了，就可以访问栈顶节点了。为了知道是否已经访问过栈顶节点的右子树，我们可以通过prev来记录上一次访问的节点。当prev等于top->right时，表示栈顶节点的右子树已经访问过了，可以弹出栈顶节点并访问它。

class Solution 
{
public:vector postorderTraversal(TreeNode* root) {vector v;stack st;TreeNode* cur = root;TreeNode* prev = nullptr;while(cur || !st.empty()){// 左路节点入栈while(cur){st.push(cur);cur = cur->left;}TreeNode* top = st.top();   // 取栈顶节点但不pop// 栈顶节点右子树为空或者上一次访问的节点是top右子树的根，说明右子树已经访问过了// 可以访问栈顶节点，否则转换成子问题访问top的右子树if(top->right == nullptr || top->right == prev){st.pop();v.push_back(top->val);prev = top;cur = nullptr;  // cur为空表示弹出的栈顶节点没有右子树或者右子树已经访问过了}elsecur = top->right;}return v;}
};

👉总结👈

本篇的非递归实现二叉树的前中后序遍历都差不多是一个思路，左路节点先入栈。最大的区别就是栈顶节点的访问时机不同。那么以上就是本篇博客的全部内容了，如果大家觉得有收获的话，可以点个三连支持一下！谢谢大家！💖💝❣️