目录

一、杨辉直角三角

                思路

                按部就班

                代码实现

二、杨辉等腰三角

注：由于VS不支持变长数组，这里我就用n=4来写

一、题目名称

题目内容：
输入一个数n，在屏幕上打印n行n列的杨辉三角。例如：输入：4输出：
1
1 1
1 2 1
1 3 3 1

二、思路

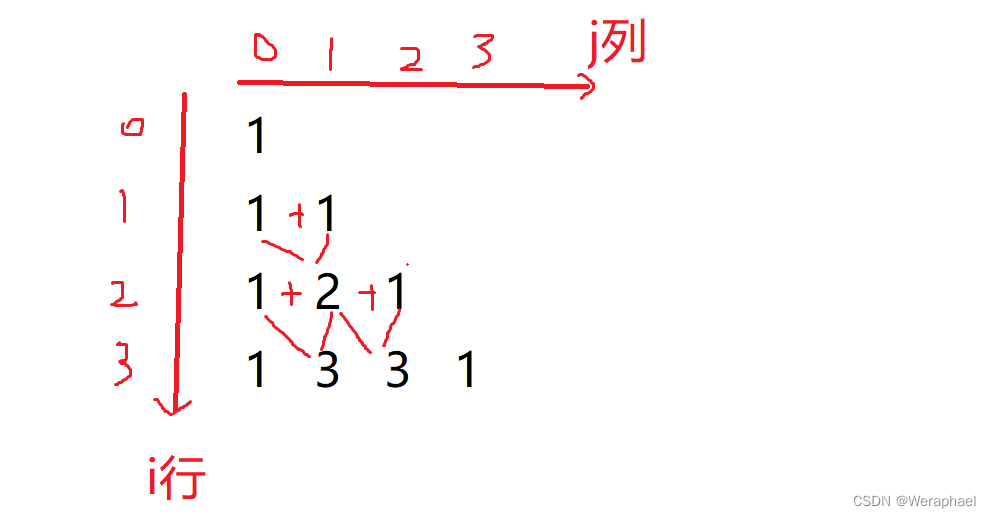
以4行4列的杨辉三角为例

首先，可以把数据存在一个i行j列的二维数组里

其次，通过规律可以发现，最左边的一列为1、斜对角线也为1

然后，如下图，中间部分都是上一行的两个相邻的数相加得到的

最后，打印出来就行了

详细的细节都在【按部就班】

三、按部就班

首先，创建一个4行4列的二维数组，并分别用i、j遍历行和列

#include 
int main()
{int arr[4][4] = { 0 };//创建二维数组并初始化for (int i = 0; i < 4; i++) {for (int j = 0; j < 4; j++){}}return 0;
}

其次，通过规律可以发现，最左边的一列为1、斜对角线也为1，所以只要将j==0或者i==j上的二维数组赋值为1即可

#include 
int main()
{int arr[4][4] = { 0 };//创建二维数组并初始化for (int i = 0; i < 4; i++) {for (int j = 0; j < 4; j++){//将斜对角线和左列赋值为1if (i == j || j == 0){arr[i][j] = 1;}}}return 0;
}

然后，中间部分都是上一行的两个相邻的数相加得到的

如上图，当i >= 2 并且 j >= 1时，中间部分通过上一行的两个相邻的数相加

#include 
int main()
{int arr[4][4] = { 0 };//创建二维数组并初始化for (int i = 0; i < 4; i++) {for (int j = 0; j < 4; j++){//将斜对角线和左列赋值为1if (i == j || j == 0){arr[i][j] = 1;}//中间部分if (i >= 2 && j >= 1){arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];}}}return 0;
}

 最后，打印出来就行了

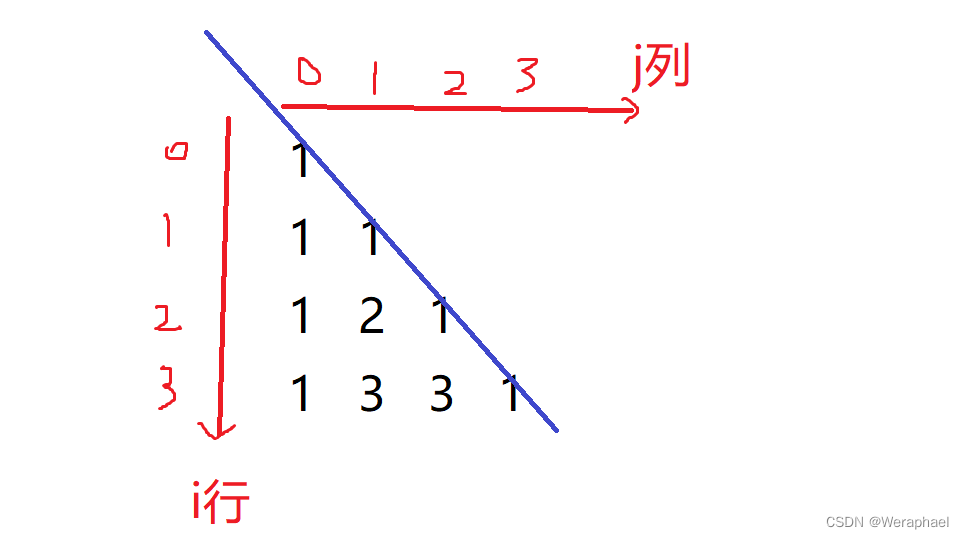
如上图，打印只要打印出斜对角线以下（包括斜对角线）的元素，也就是i >= j即可，别忘了打印完一行需要换行

【代码实现】

#include 
int main()
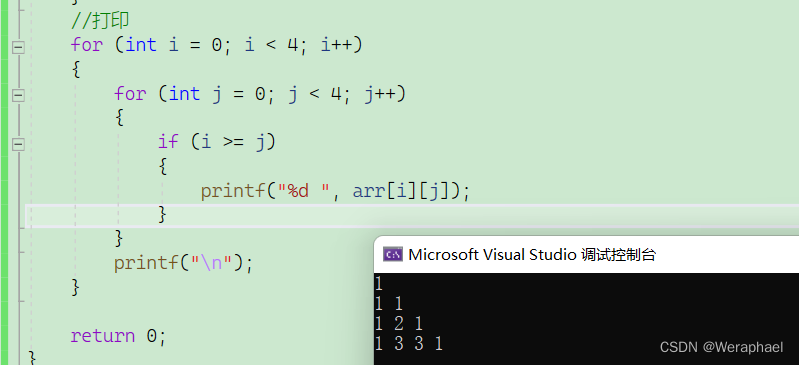
{int arr[4][4] = { 0 };//创建二维数组并初始化for (int i = 0; i < 4; i++) {for (int j = 0; j < 4; j++){//将斜对角线和左列赋值为1if (i == j || j == 0){arr[i][j] = 1;}//中间部分if (i >= 2 && j >= 1){arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];}}}//打印for (int i = 0; i < 4; i++){for (int j = 0; j < 4; j++){if (i >= j){printf("%d ", arr[i][j]);}}printf("\n");}return 0;
}

程序运行结果：

 四、杨辉直角三角

这个和打印菱形差不多，大家可以去参考 ---->  打印菱形（我还在评论区给出一个打印圣诞树的OJ链接，也和这个很像）

这里我就直接给出代码了

#include int main()
{int arr[4][4] = { 0 };//创建二维数组并初始化for (int i = 0; i < 4; i++){for (int j = 0; j < 4; j++){//将斜对角线和左列赋值为1if (i == j || j == 0){arr[i][j] = 1;}//中间部分if (i >= 2 && j >= 1){arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];}}}//和打印菱形差不多for (int i = 0; i < 4; i++){//先打印空格for (int j = 0; j < 4 - 1 - i; j++){printf(" ");}//打印数字for (int j = 0; j <= i; j++){printf("%d ",arr[i][j]);}printf("\n");}return 0;
}

程序效果：

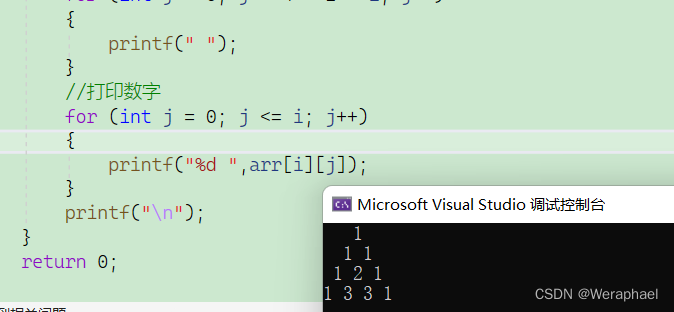
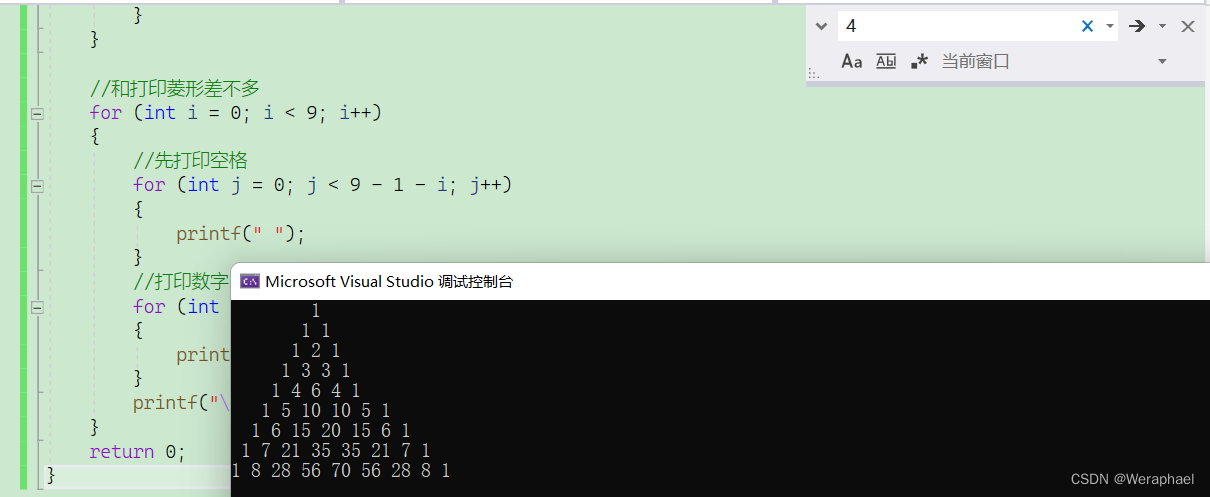
因为vs不支持变长数组，若要打印n行n列，就把4换掉就行

比如打印9行9列

 2023年1月18日