Apollo studio 官网：Apollo开发者社区 (baidu.com)

星火计划2.0基础课：Apollo星火计划2.0_Apollo精品课 (baidu.com)
星火计划2.0专项课：Apollo星火计划之PnC专项_Apollo精品课 (baidu.com)

目录

1 参考线的作用

2 参考线的数据结构

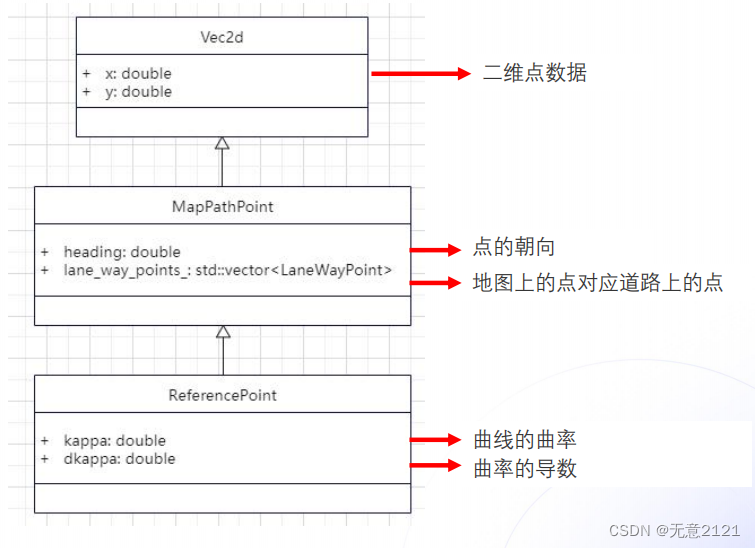
2.1 ReferenceLine的数据结构 

2.2 ReferencePoint的数据结构

3 参考线处理流程

​4 参考线平滑算法

4.1 算法分类

4.2 参考线平滑算法流程

4.2.1 AnchorPoint

4.2.2 smooth

4.2.3 solve 

5 具体算法 

1 参考线的作用

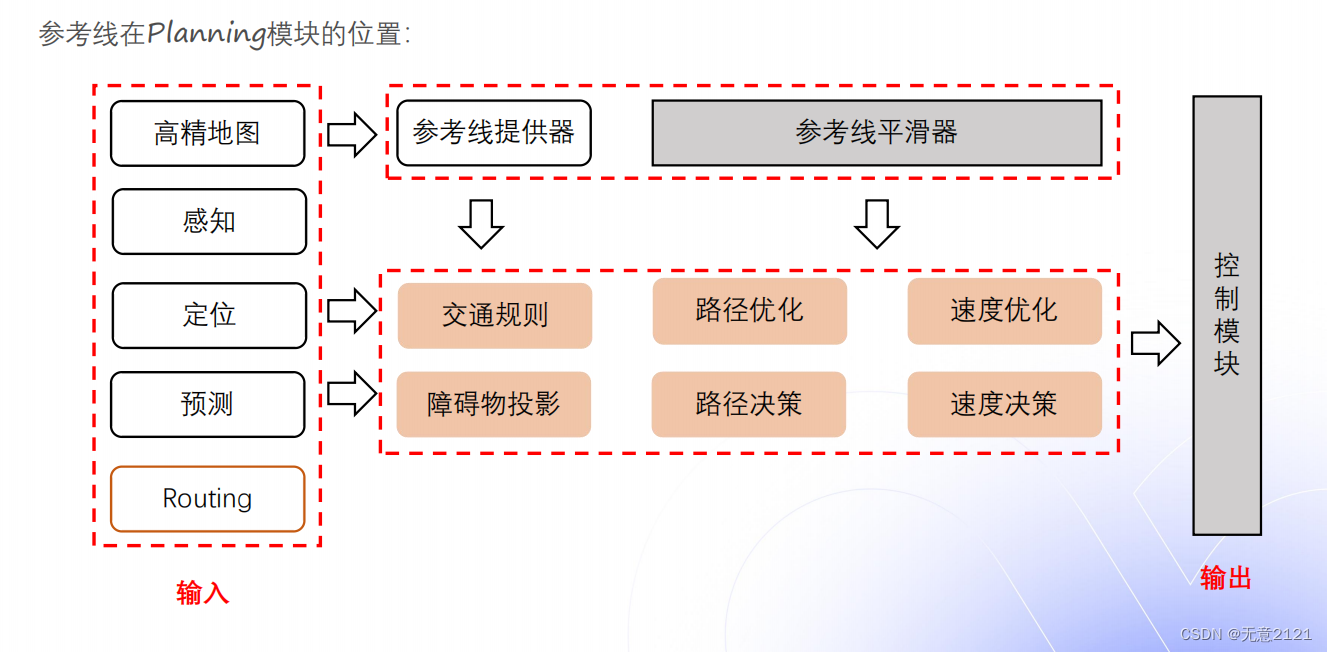
参考线在planning中的作用相当于一个地基，所有决策与优化都是在参考线的基础上进行

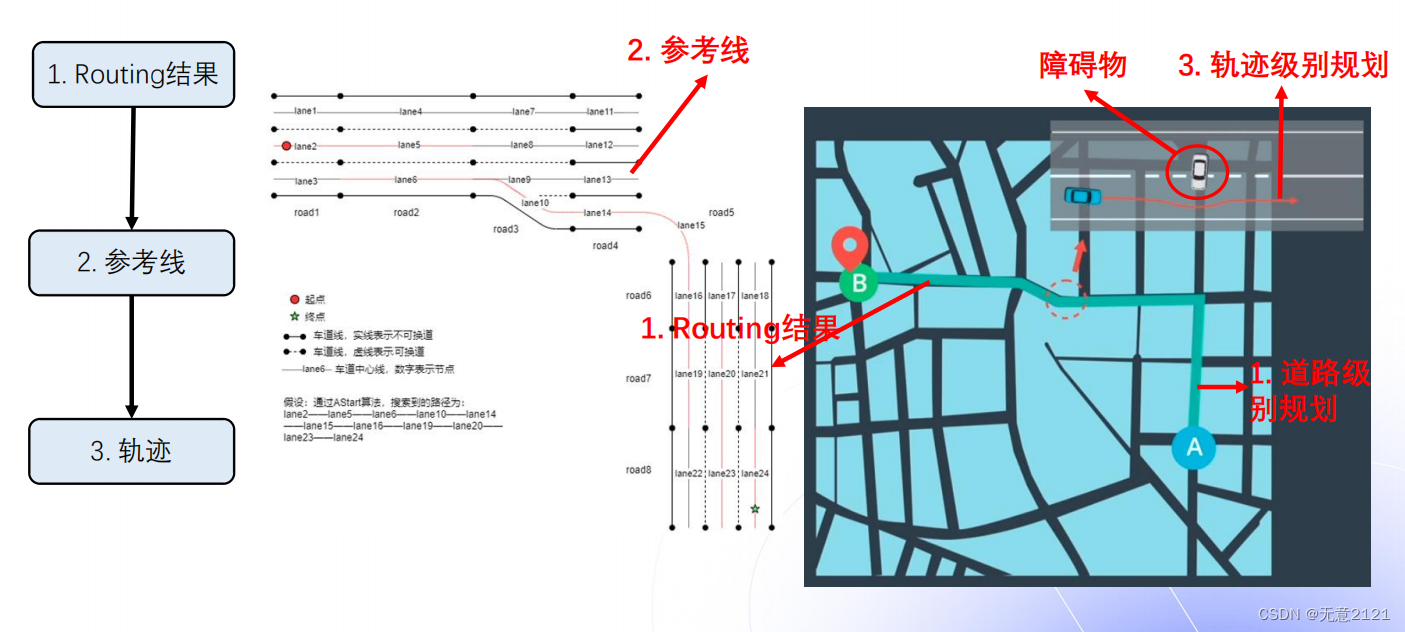
• Routing利用A*进行车道级别的规划
• 再对每一个车道赋予参考线，最后得到了车道级别的参考线
• 最后则是planning模块输出轨迹级别的规划结果

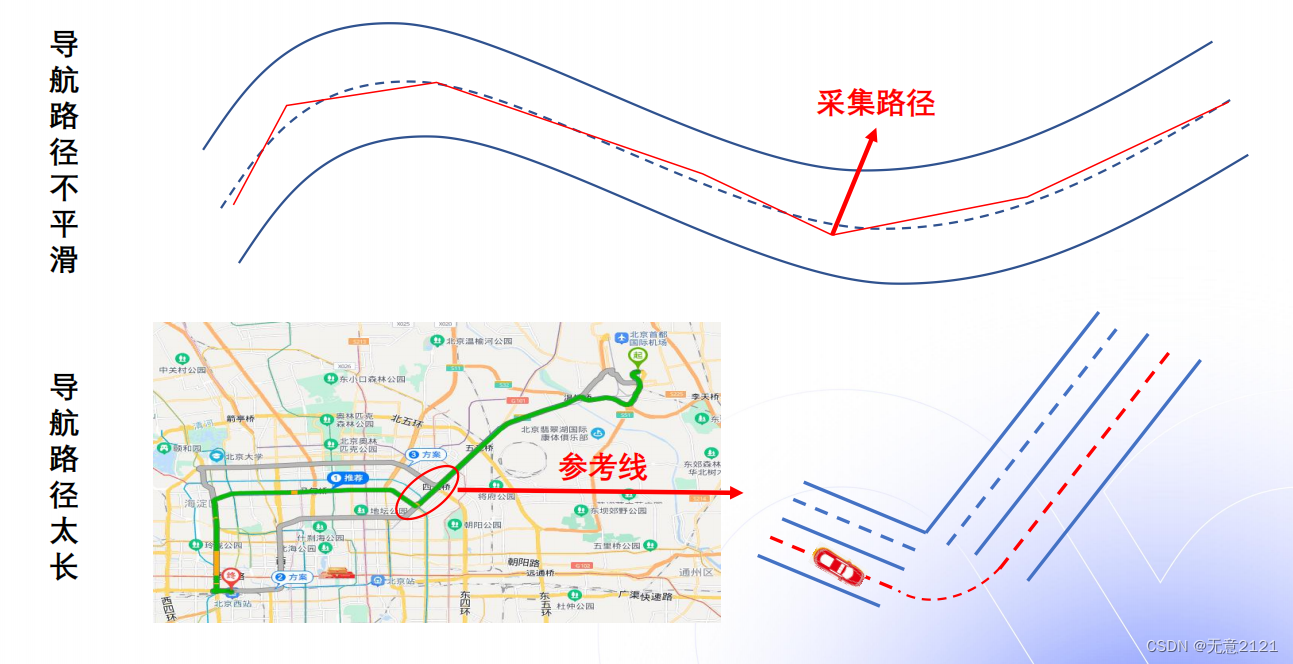
• HD map一般都是人为采集离散点，也就使得原始路径不平滑
• 同时全局导航的路径过长，障碍物的投影点也可能不唯一
• 所以我们需要生成一个局部的一定长度且光滑的参考线，也节省了算力

2 参考线的数据结构

2.1 ReferenceLine的数据结构 

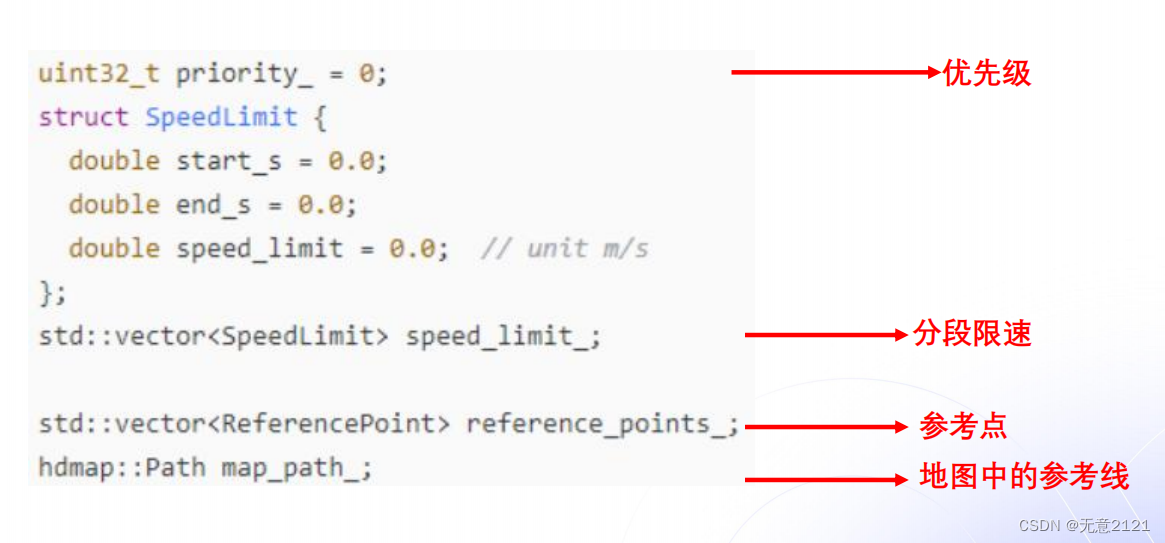
2.2 ReferencePoint的数据结构

3 参考线处理流程

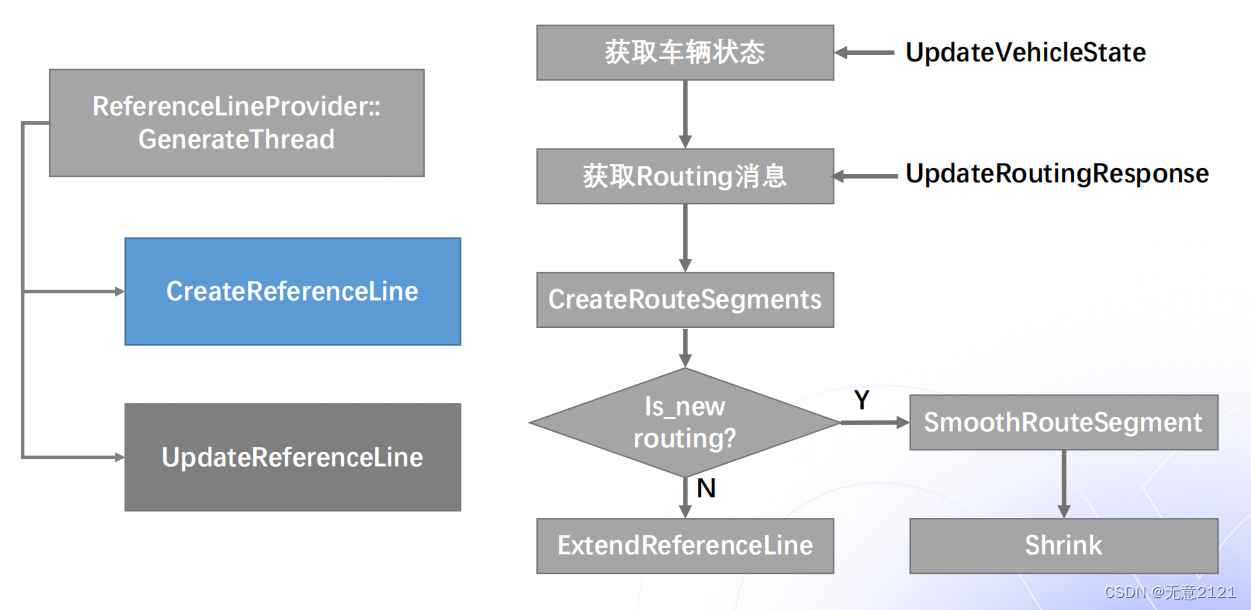
 参考线处理分两步

1. 生成参考线，这主要由Routing模块的输出决定
2. 参考线平滑，接下来会详细讲解参考线的平滑的算法

4 参考线平滑算法

4.1 算法分类

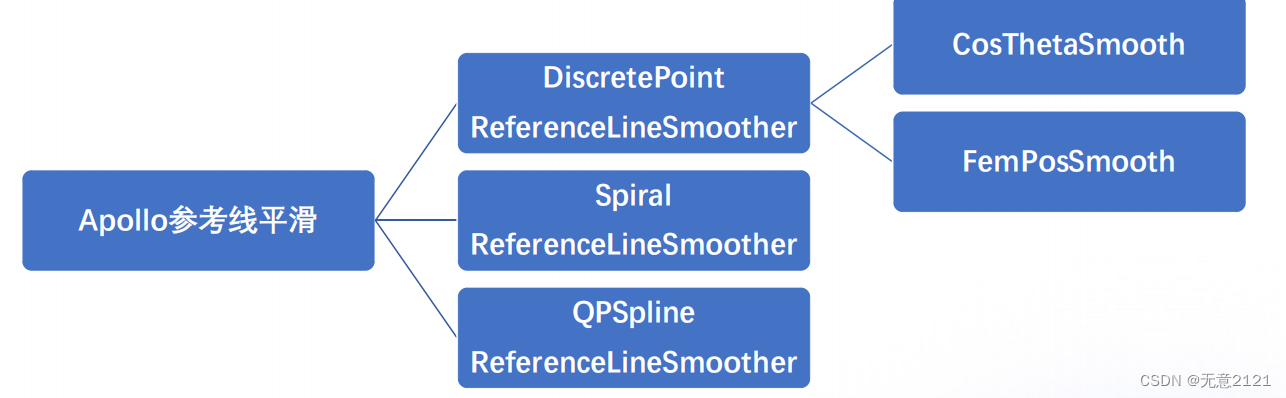
参考线平滑算法主要有三种

• 离散点平滑
• 螺旋曲线平滑
• 多项式平滑 

  if (smoother_config_.has_qp_spline()) {smoother_.reset(new QpSplineReferenceLineSmoother(smoother_config_));} else if (smoother_config_.has_spiral()) {smoother_.reset(new SpiralReferenceLineSmoother(smoother_config_));} else if (smoother_config_.has_discrete_points()) {smoother_.reset(new DiscretePointsReferenceLineSmoother(smoother_config_));} else {ACHECK(false) << "unknown smoother config "<< smoother_config_.DebugString();}is_initialized_ = true;

 这里是对参考线平滑算法进行配置，Apollo系统中默认采用离散点平滑算法

4.2 参考线平滑算法流程

bool ReferenceLineProvider::SmoothReferenceLine(const ReferenceLine &raw_reference_line, ReferenceLine *reference_line) {if (!FLAGS_enable_smooth_reference_line) {*reference_line = raw_reference_line;return true;}// generate anchor points:std::vector anchor_points;GetAnchorPoints(raw_reference_line, &anchor_points);smoother_->SetAnchorPoints(anchor_points);if (!smoother_->Smooth(raw_reference_line, reference_line)) {AERROR << "Failed to smooth reference line with anchor points";return false;}if (!IsReferenceLineSmoothValid(raw_reference_line, *reference_line)) {AERROR << "The smoothed reference line error is too large";return false;}return true;
}

输入raw_reference_line，设置中间点（GetAnchorPoints），然后smooth，最后输出

4.2.1 AnchorPoint

struct AnchorPoint {common::PathPoint path_point;double lateral_bound = 0.0;double longitudinal_bound = 0.0;// enforce smoother to strictly follow this reference pointbool enforced = false;
};

 lateral_bound、longitudinal_bound代表裕度，enforced代表是否是强约束 

max_constraint_interval : 0.25
longitudinal_boundary_bound : 2.0
max_lateral_boundary_bound : 0.5
min_lateral_boundary_bound : 0.1
curb_shift : 0.2
lateral_buffer : 0.2

这是中间点的配置文件

4.2.2 smooth

bool status = false;const auto& smoothing_method = config_.discrete_points().smoothing_method();std::vector> smoothed_point2d;switch (smoothing_method) {case DiscretePointsSmootherConfig::COS_THETA_SMOOTHING:status = CosThetaSmooth(raw_point2d, anchorpoints_lateralbound,&smoothed_point2d);break;case DiscretePointsSmootherConfig::FEM_POS_DEVIATION_SMOOTHING:status = FemPosSmooth(raw_point2d, anchorpoints_lateralbound,&smoothed_point2d);break;default:AERROR << "Smoother type not defined";return false;}if (!status) {AERROR << "discrete_points reference line smoother fails";return false;

bool DiscretePointsReferenceLineSmoother::FemPosSmooth(const std::vector>& raw_point2d,const std::vector& bounds,std::vector>* ptr_smoothed_point2d) {const auto& fem_pos_config =config_.discrete_points().fem_pos_deviation_smoothing();FemPosDeviationSmoother smoother(fem_pos_config);// box contraints on pos are used in fem pos smoother, thus shrink the// bounds by 1.0 / sqrt(2.0)// 裕度收缩std::vector box_bounds = bounds;const double box_ratio = 1.0 / std::sqrt(2.0);for (auto& bound : box_bounds) {bound *= box_ratio;}std::vector opt_x;std::vector opt_y;// 问题求解bool status = smoother.Solve(raw_point2d, box_bounds, &opt_x, &opt_y);if (!status) {AERROR << "Fem Pos reference line smoothing failed";return false;}if (opt_x.size() < 2 || opt_y.size() < 2) {AERROR << "Return by fem pos smoother is wrong. Size smaller than 2 ";return false;}

4.2.3 solve 

bool FemPosDeviationSmoother::Solve(const std::vector>& raw_point2d,const std::vector& bounds, std::vector* opt_x,std::vector* opt_y) {// 考虑曲率约束if (config_.apply_curvature_constraint()) {if (config_.use_sqp()) {// 线性求解return SqpWithOsqp(raw_point2d, bounds, opt_x, opt_y);} else {// 非线性求解return NlpWithIpopt(raw_point2d, bounds, opt_x, opt_y);}}// 不考虑曲率约束 else {// 线性求解（默认）return QpWithOsqp(raw_point2d, bounds, opt_x, opt_y);}return true;
}

5 具体算法 

r

离散点平滑算法也是基于评价函数来做的，分别衡量

• 曲线平滑度
• 曲线长度
• 点与参考点的误差

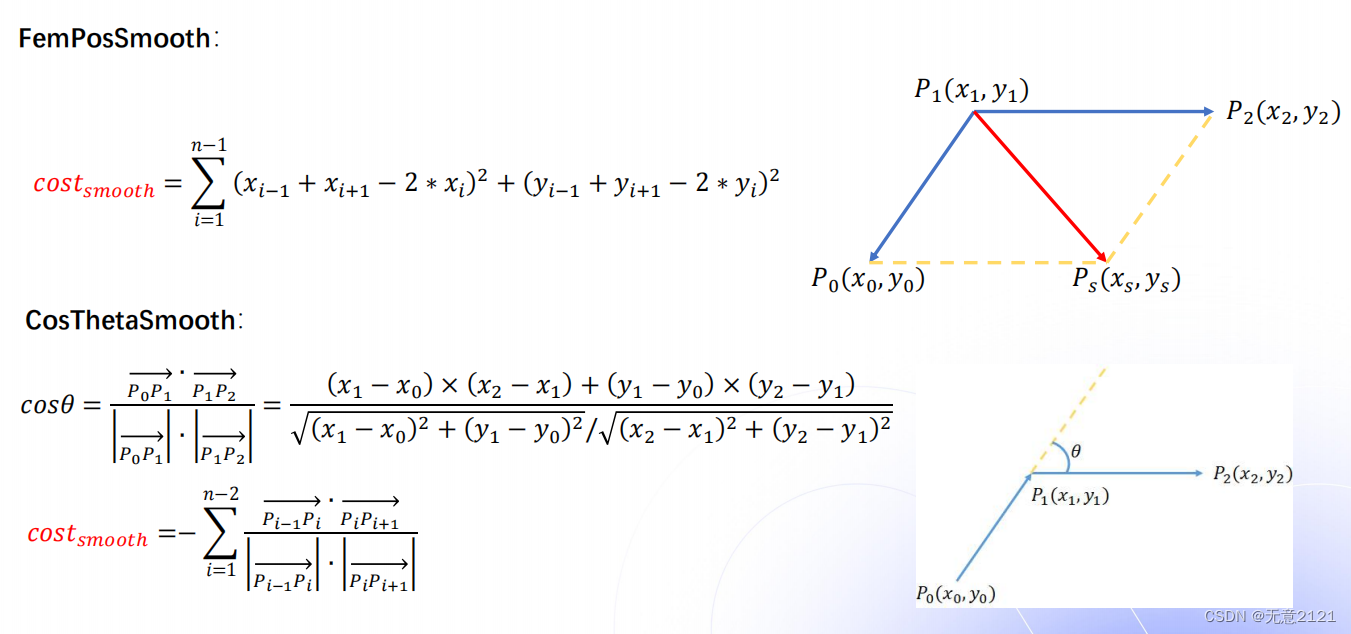
对于平滑度的衡量有两种方式

• FemPosSmooth相对不精准，但是只需用二次规划能快速求解
• CosThetaSmooth相对精准，但是需要非线性规划，计算量大 

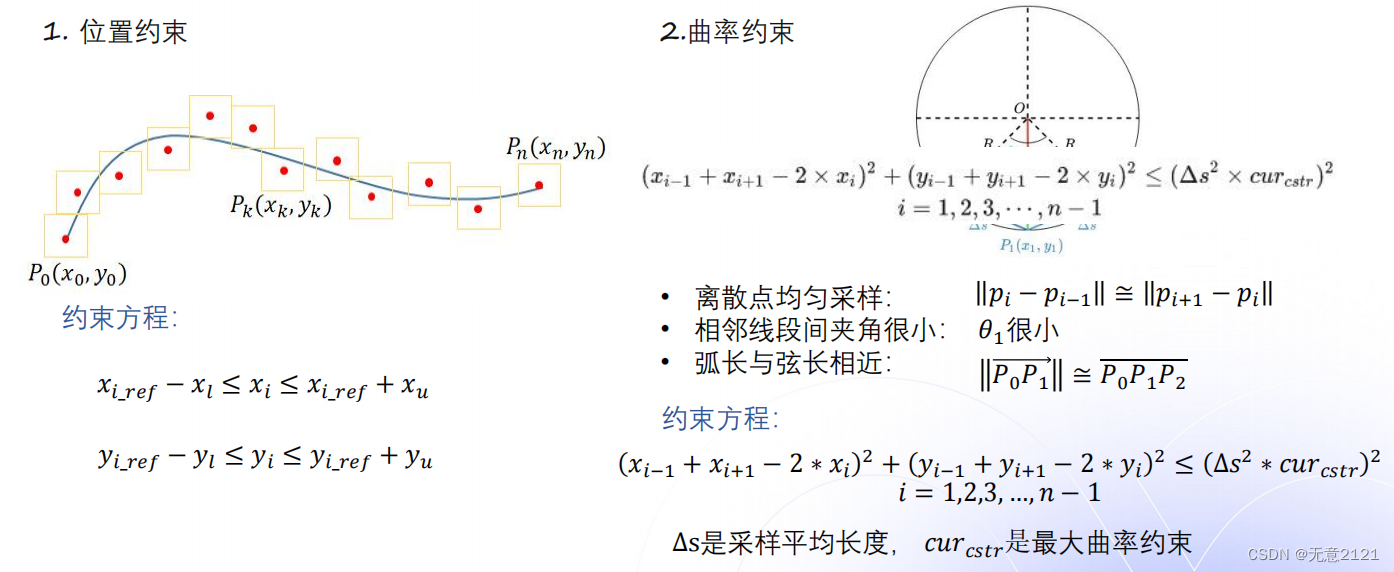 同时还需要满足约束条件

• 位置约束保证离散点相对于原来的不过于偏离
• 曲率约束使得参考线曲率尽量符合车辆运动学约束，易于跟踪