ACWING寒假每日一题

有些题是蓝桥杯的题，在之前的文章已经写过这里就不再写了

一、孤独的照片

一个点一个点的来看，比如对于GHGHG中间的G，找到他的左边的G，以及右边的G的位置，l,r分别等于1，答案就要多加上11
但是如果对于 GHHGHHG 中间的G，我们可以看到l,r等于2，那么就一个中间G的对于他的左半边来说，能拍l-1张照片，右半边也是能拍r-1张，之后左右一起看的话能拍lr张。
知道这个就好做了，我们只需要把每个G和H点的坐标存起来，然后遍历一编就行了，不过要注意边界，例如对于第一个G点，他的l是等于他的坐标的，那么我们只需要把G[0]设置为-1，这样计算l的时候就会等于G[1]（l = g[i] - g[i-1] -1）

具体代码如下

n = int(input())
s = input()
res = 0
g,h = [-1],[-1]  # 第一个点 h[1] - h[1-1]-1 就是h[1]
for i in range(n):if s[i] == 'G':g.append(i)  # 记录G的位置else:h.append(i)  # H的位置
g.append(n)  # 处理右边界， 最后一个点 h[i+1]-h[i]-1 
h.append(n)
for i in range(1,len(g)-1):l = g[i] - g[i-1] - 1 r = g[i+1] - g[i] - 1if l >= 2:res += l-1if r >= 2:res += r-1res += r*l
for i in range(1,len(h)-1):l = h[i] - h[i-1] - 1 r = h[i+1] - h[i] - 1if l >= 2:res += l-1if r >= 2:res += r-1res += r*lprint(res)

二、统计次数

对于python来说并不难，我们有count函数，其他语言我就不知道了，O（n）时间复杂度

代码如下

n,k = map(int,input().split())
res = 0
for i in range(1,n+1):i = str(i)k = str(k)res += i.count(k)
print(res)

三、上课睡觉

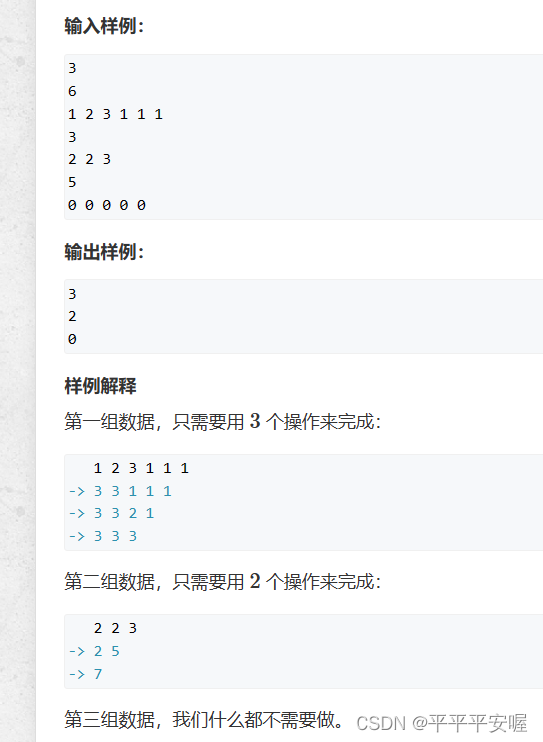
对于每组数据，我们从大到小遍历堆数，就是总共要合成成几堆，假设为K堆，那么我们需要的操作就是n-k,因为k从大到小，所以我们找到的一定是操作数最少的。
假设分为k堆，首先要判断总数sum % k 是否等于0，如果不等于代表他不能被k等分，就不行
如果可以的话，因为只有相邻的合并，所以我们从小到大遍历石堆，设置一个遍历m m 去 += w[i],w为石堆，然后如果等于 sum // k 就让m归0，继续往下找，如果m>sum//k 那就肯定不行了，然后最后如果m == 0 代表最后合成的一堆也等于 sum // k ，就成功拉。

PS：可能说的有点乱，总的来说就是需要遍历石堆里的，然后从头到尾合并，都合并成sum//k，如果合并着合并着发现大于sum//k了，那就肯定不行了，因为你如果舍弃掉开头那个，就算你这堆可以等于sum//k，但是你开头那个就没办法和别的石子合并了。因为这堆的开头的那个石子的前面要么没石头，要么它的前面已经合并为sum//k了。

#### 代码如下def solve(w,cnt,totle):if totle % cnt != 0: return False# 如果总数不能除尽堆数，证明这个堆数是不可能的k = totle // cntm = 0for i in range(len(w)):m += w[i]if m > k : return Falseif m == k : m = 0return m == 0    # 如果最后面刚好最后一堆的总和也等于平均数，就返回Trueif __name__ == '__main__':t = int(input())for i in range(t):n = int(input())w = [int(x) for x in input().split()]totle = sum(w)for cnt in range(n,0,-1) : # 遍历堆数 就是要多最多的堆if solve(w,cnt,totle) : print(n - cnt)     # 例如5堆最后分为3堆，就要操作5-2次break

四、学分绩点

这题也是比较暴力的题，就没什么好说的

代码如下

if __name__ == '__main__':n = int(input())xuefen = [int(x) for x in input().split()]scores = [int(x) for x in input().split()]res = 0for i in range(n):if scores[i] >= 90:res += xuefen[i] * 4.00elif scores[i] >= 85:res += xuefen[i] * 3.7elif scores[i] >= 82:res += xuefen[i] * 3.3elif scores[i] >= 78:res += xuefen[i] * 3.0elif scores[i] >= 75:res += xuefen[i] * 2.7elif scores[i] >= 72:res += xuefen[i] * 2.3elif scores[i] >= 68 :res += xuefen[i] * 2.0elif scores[i] >= 64:res += xuefen[i] * 1.5elif scores[i] >= 60:res += xuefen[i] * 1.0else: res += 0print('{:.2f}'.format(res/sum(xuefen)))

五、奶牛大学

将每头奶牛愿意出的学费给排序一下，然后一个个去遍历，以第一个，第二个…作为学费，找到最大值，用enumerate就会很方便，例如以第三头牛的愿意出的最大价格做学费，sum = 学费 *（n-i） 。如果有重复的不用担心，例如愿意出的最大价格排好序后是 1 3 3 3 … 那么在计算第一个3的时候，就是学费为3的能赚到钱的最大值，后面两个不会覆盖掉第一个3

代码如下

if __name__ == '__main__':n = int(input())s = [int(x) for x in input().split()]s.sort()maxsum = 0finalmoney = 0for i,money in enumerate(s):sum = money * (n-i)if sum>maxsum:maxsum = sumfinalmoney = moneyprint(maxsum,finalmoney)

六、选数异或

直接暴力的话肯定会TLE的，我们先预处理一个数组 maxl ，maxl[i] 代表右边界为i， 能容忍的左边界最大是多少，如果最后 l > maxl[r] ，就 say no 了 ，因为你比我能容忍的最大还大。
那要怎么算这个maxl呢，首先如果第i个数的异或x的值假设为b，maxl[i - 1] 表示前一个位置能容忍的最大值，那么maxl[i] 是不是要等于 max( maxl[i-1] , b的最后一个位置)。
那么我们现在只需要算出前面出现过的数的最后一个位置就行了，再建立一个endpos表示每个数的最后一个位置。在遍历的时候让endpos[arr[i]] = i 就行（arr为原数组）
又因为l和r是从1开始的，所以我们的原始数组arr应该也从坐标1开始，在第一个位置上加个-1就行。

具体代码如下

## a ^ b = x  --> a ^ x = b
N = 10**7
if __name__ == '__main__':n,m,x = map(int,input().split())endpos = [-1] * Narr = [-1]+[int(x) for x in input().split()]maxl = [-1] * (n+2)for i in range(1,n+1):# 对于每个位置来说，他能容许的左边的最大值（l 不能比这个再大了，可以在它的左边）是 maxl[i - 1] 或者 它目前这个位置的数异或值的最后一个位置maxl[i] = max(maxl[i-1] , endpos[arr[i]^x])  # arr[i] ^ x 是你这个点想要的那个b arr[i] ^ b = x,endpos[b] 就表示b出现的最后位置endpos[arr[i]] = i  # 记录一下每个数字出现的最后位置，每个重复数字都记录的是后面那个数字的下标for i in range(m):l,r = map(int,input().split())if (l != r and maxl[r] >= l):print('yes')else: print('no')

七、求和

想通了就很简单拉，a1 会 乘以 a2 a3 a4 … ，a2 乘以 a3 a4 …

直接看代码把

n = int(input())
a = [int(x) for x in input().split()]
sum1 = sum(a)
## 计算a1*a2+...a1*an+a2*a1+..a2*an...最后除以2
res = 0
for x in a:res += x*(sum1-x)
print(res >> 1)

八、数位排序 （蓝桥杯2022）

九、重新排序

要算重新排序后最大的和，我们只需要看看每个位置上最被加了多少编，然后把最大的值放在被加了最多的位置上就好了，每个位置被加了多少遍可以用差分来做。把最大的值放在被加了最多的位置上可以上数组和每个位置上被加了多少次都分别排序，这样一一对应相乘就OK了

具体代码如下

n = int(float(input()))
A = [int(x) for x in input().split()]
s = [0]*(n+1)
for i in range(1,n+1):s[i] = s[i-1] + A[i-1]
m = int(input())
C = [0]*(n+1) # 用来存储每个数被查询了几次，差分
sum0 = 0
for i in range(m):a,b = map(int,input().split())# for i in range(a-1,b):  # 数组中的下标要-1#     sum0 += A[i]#     C[i] += 1sum0 += (s[b] - s[a-1])C[a-1] += 1C[b] -=1
for i in range(1,n):C[i] += C[i-1]
C = C[:n]
A.sort()
C.sort()
sum1 = 0
for i in range(n):sum1 += C[i]*A[i]
print(sum1 - sum0)

十、纸张尺寸（蓝桥杯2022）

十一、技能升级（蓝桥杯2022）

十二、未初始化警告

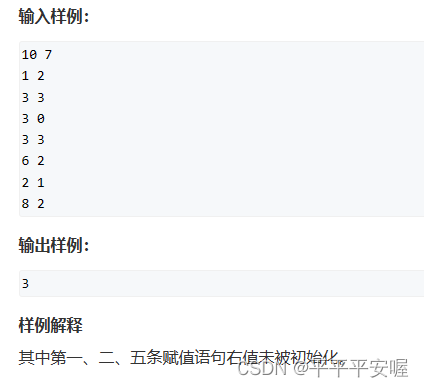
感觉没啥好说的嗯,就直接看代码把，肯定能看懂

代码如下

n,k = map(int,input().split())
left = [] 
right = []
for _ in range(k):l,r = map(int,input().split())left.append(l)right.append(r)
res = 0
for i in range(k):r = right[i]if i == 0 and r != 0 : res += 1continue if r == 0:continueif r not in left[:i] : res += 1
print(res)

十三、归一化处理

这题对Python来说就很简单，他本身就不用考虑小数点后面几位什么什么的，直接做就行

代码如下

import math
n = int(input())
A = [int(x) for x in input().split()]
a = sum(A) / n
d = 0
for i in range(n):d += (A[i] - a) ** 2
d = d/n
sqrtd = math.sqrt(d)
for i in range(n):print((A[i] - a) / sqrtd )

十四、如此编码

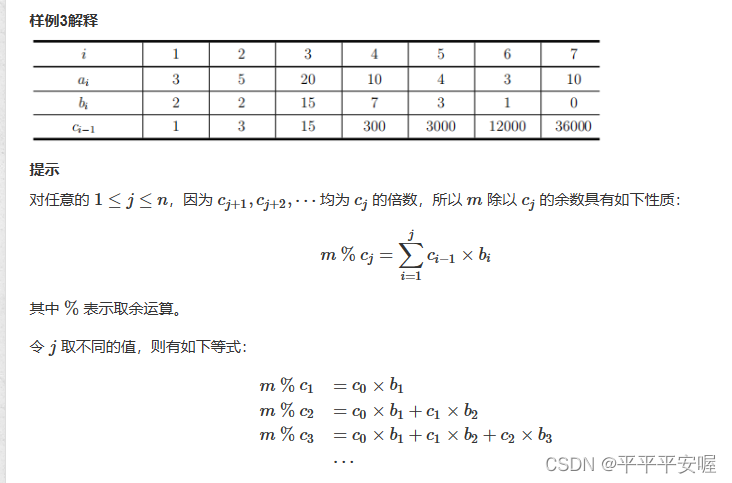
可以看到，m % c1 // c0 就会等于b1 那么b2 等于什么呢？
b2 = m % c2 // c1 一位内 c0*b1 = m % c1 他一定不会大于c1了，所以他可以忽略不计
这样的话就好做了，我们只需要记录一个ci 和一个 c(i-1) 就行拉

具体代码如下

n,m = map(int,input().split())
a = [int(x) for x in input().split()]
b = []
c = 1 # c0 = 1
tc = 1
for i in a:tc = i*c  # 第一次是c1,c是c0，第二次t是c2，c是c1，以此类推b.append((m%tc) // c)c = tc
print(*b)

十五、何以包邮？

我们用f[j]表示价格为j的方案是否存在，存在为1，否则为0
之后我们只需要遍历一下我们的书的价格的数组，从很大到他的价格使得 f[j] |= f[j - w[i]]，从大到小就不会买同一本书，f[j - w[i]] 是1 ，那么就代表我们可以买下w[i]这本书，使得f[j] = 1

具体代码如下

# f[i]表示价格为i的方案是否存在
n,x = map(int,input().split())
w = []
for _ in range(n):money = int(input())w.append(money)maxxx = 3*10**5 + 10
f = [0]*(maxxx + 1000)
f[0] = 1
for i in range(n):for j in range(maxxx,w[i]-1,-1):f[j] |= f[j - w[i]]
for i in range(x,maxxx+1):if f[i] == 1:print(i)break 

十六、出行计划

借用一下大佬的解释

也就是说 对于第i个场所，q如果在一个ti - k - ci +1 到 ti - k 范围内，就代表可以去到这个地方。
那么我们就可以用差分了，对于每个场所，我们把d 数组从ti - k - ci +1 到 ti -k 这件的数都+1，最后只要求一下d[q] 就好了。

具体代码如下

n,m,k = map(int,input().split())
N  = 10 ** 6
d = [0] * N
for _ in range(n):t,c = map(int,input().split())d[max(1,t-k-c+1)] += 1d[max(1,t-k+1)] -= 1for i in range(1,N):d[i] +=d[i-1]     # 前缀和for _ in range(m):q = int(input())print(d[q])

十七、寻宝！大冒险！

我们可以记录下绿化图每个树的点，切记不能直接把图画出来，那样太大了会爆内存。
然后因为藏宝图左下角一定是课树，我们可以遍历绿化图中所有的树，然后从他延申看看是否符合，是否符合就比较简单了，遍历一下i,j 长度为s 如果藏宝图[i][j] 为1，那就找对应的绿化图中是否有树。

具体代码如下

n,l,s = map(int,input().split())
# green = [[0]*(l+1) for _ in range(l+1)]  # 直接建立个列表会超内存，因为要建立10**p * 10**9 的列表 太大了
treasure =  [[] for _ in range(s+1)]
tree = []
map1={}     # map1跟tree作用差不多，但是后面要找元素是否在map1中，这比找是否在tree中快
for _ in range(n):x,y = map(int,input().split())tree.append((x,y))map1[(x,y)]=1# green[x][y] = 1
for i in range(s+1):a = [int(x) for x in input().split()]treasure[s-i] = a
res = 0for x,y in tree:flag = 0for i in range(s+1):for j in range(s+1):if x + i > l or y + j > l : flag = 1if treasure[i][j] :if (x+i,y+j) not in map1:flag = 1breakelse: if (x+i,y+j) in map1:flag = 1breakif flag == 1:breakif flag == 1:continueelse : res += 1print(res)

十八、左孩子右兄弟（蓝桥杯2021）

十九、乘方

这个也比较简单拉，直接看代码把

具体代码如下

a,b = map(int,input().split())
res = 1
for _ in range(1,b+1):res *= aif res > 1000000000 :print(-1)break
if res <= 1000000000:print(res) 

二十、解密

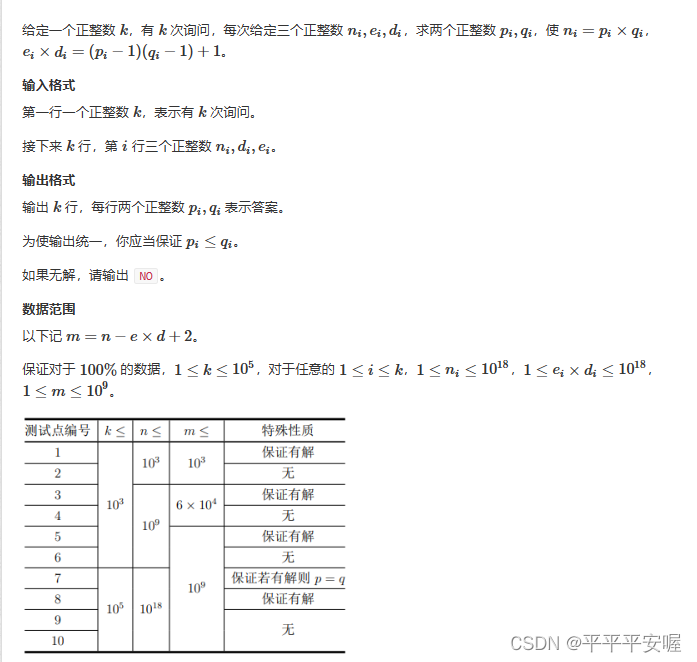
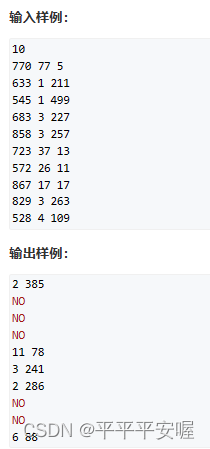
直接看一下大佬moyou的数学推导把。。太强了

直接根据这些公式写就好了。。

具体代码如下

from math import sqrt 
for _ in range(int(input())):n,d,e = map(int,input().split())m = n - d*e + 2delta = m*m - 4*nif delta < 0:print('NO')else:x = sqrt(delta)if x == int(x):up1 = m - xup2 = m + xif up1 % 2 == 0 and up2 % 2 == 0:print(int(up1 / 2), int(up2 / 2))else:print('NO')else: print('NO')