高数:数列的收敛
创始人
2024-05-28 21:30:29
数列特点
无限个数
特定顺序
数列和集合区别
集合可以乱序,数列不行
集合出现重复元素依然相同,数列出现新的重复元素就不相等
[1,2,3,4]=[1,2,3,3,4]
对集合来说相等,对数列来说不相等。
数列的表示形式

求数列的单调性
作差,作商,求导,列举法,把极限和某项比较。
有界数列有上界和下界
如何证明一个数列无界?
eg:比较审敛法
2^n+1>2^n
2^n趋于无穷,2^n+1趋于无穷
证明数列收敛
直接证明数列极限
找出N和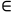 的关系
的关系

夹逼准则

夹逼准则的推论:如果数列的绝对值趋近于0,数列趋于零。
当数列的符号无法确定时,用绝对值证
洛必达法则,无穷/无穷或0/0
洛必达法则是:量级的比较和同除n^p有异曲同工之妙。
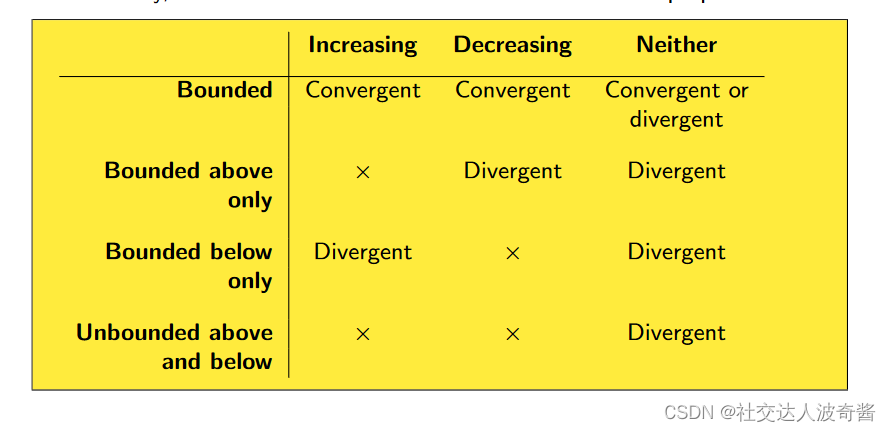
数列单调且有界,数列收敛
数列和的收敛
数列和收敛,数列趋近于0,但数列趋近于0,数列不一定收敛。
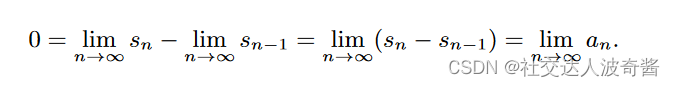
积分试验:
被积的函数是递减函数,函数的反常积分收敛,等于函数各项和收敛。
(两个其实表示的都是函数围成的面积。)
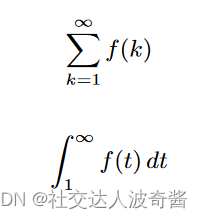
使用时先判断是否是递减,在再使用。递减是为了保证大小关系
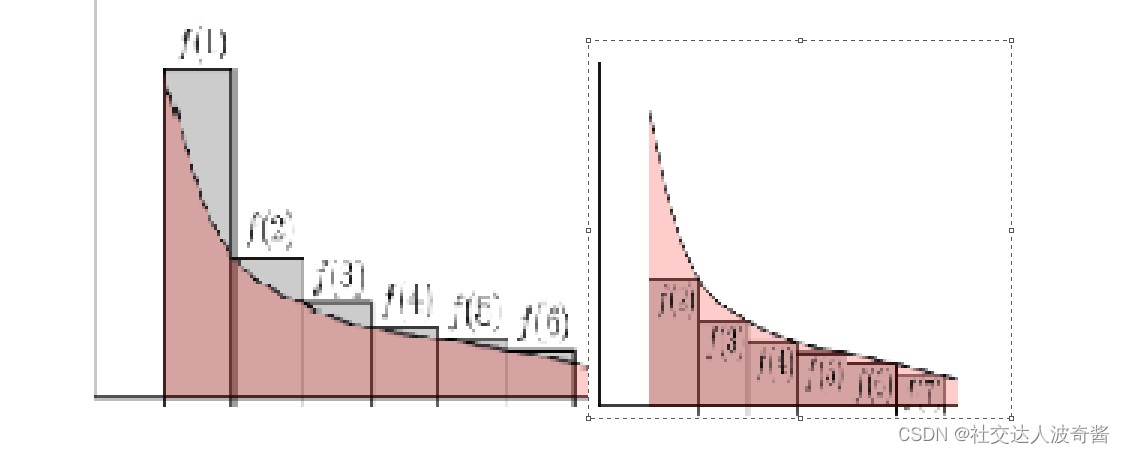
去掉最左边那一块,右边能全部移到左边,此时曲线面积大于数列和面积,证明反常积分收敛,就能证明数列和收敛(从第二项开始的和收敛和第一项开始收敛是一样的)
比较审敛法:同反常积分。
交错级数判别法:
交错级数:一正一负
1,-2,3,-4...
-1,2,-3,-4……
证明交错级数收敛
证明数列的绝对值:1.单调递减或最终单调递减 2.收敛于0。
一些公式及技巧
单调减的指数函数乘幂函数的收敛于0

证明:一直洛必达法则直到幂函数的系数为0。
由于指数的变化速率太快,使得幂函数的a是1或者k都一样。
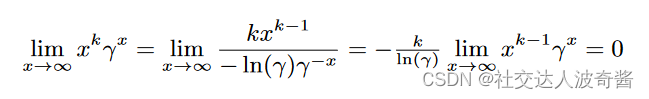
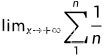 的结果
的结果
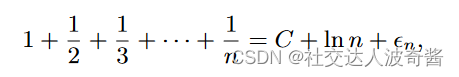
n为项数,C为欧拉常数用来调和级数
习题
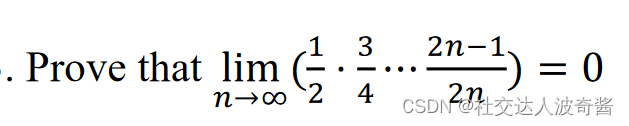
累乘无法相消,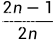 的极限趋向于1。
的极限趋向于1。
这意味着无法对每一项放缩成再相乘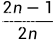 只能整体放缩
只能整体放缩
注意:
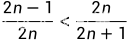
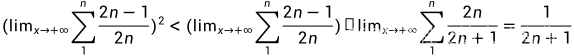
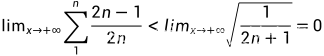
巧妙的放缩!
下一篇:数据结构基础之链表
相关内容
热门资讯
苗族的传统节日 贵州苗族节日有...
【岜沙苗族芦笙节】岜沙,苗语叫“分送”,距从江县城7.5公里,是世界上最崇拜树木并以树为神的枪手部落...
长白山自助游攻略 吉林长白山游...
昨天介绍了西坡的景点详细请看链接:一个人的旅行,据说能看到长白山天池全凭运气,您的运气如何?今日介绍...
世界上最漂亮的人 世界上最漂亮...
此前在某网上,选出了全球265万颜值姣好的女性。从这些数量庞大的女性群体中,人们投票选出了心目中最美...
阿西吧是什么意思 阿西吧相当于...
即使你没有受到过任何外语培训,你也懂四国语言。汉语:你好英语:Shit韩语:阿西吧(아,씨발! )日...
猫咪吃了塑料袋怎么办 猫咪误食...
你知道吗?塑料袋放久了会长猫哦!要说猫咪对塑料袋的喜爱程度完完全全可以媲美纸箱家里只要一有塑料袋的响...
