1 两数之和

1.1 题目描述

        题目链接：https://leetcode.cn/problems/two-sum/description/

1.2 求解思路

1. 暴力枚举

        最容易想到的方法是枚举数组中的每一个数 x，寻找数组中是否存在 target - x

参考代码

class Solution(object):def twoSum(self, nums, target):n = len(nums)for i in range(n):for j in range(i+1, n):if nums[i]+nums[j]==target:return [i, j]

2. 哈希表

        创建一个哈希表，对于每一个 x，我们首先查询哈希表中是否存在 target - x，然后将 x 插入到哈希表中，即可保证不会让 x 和自己匹配。

参考代码

class Solution:def twoSum(self, nums: List[int], target: int) -> List[int]:hash_dict = dict()for i, num in enumerate(nums):if target - num in hash_dict:return [hash_dict[target - num], i]else:hash_dict[num] = i

2 两数之和-输入有序数组

2.1 题目描述

        题目链接：https://leetcode.cn/problems/corporate-flight-bookings/

2.2 思路分析

1. 二分查找

        在数组中找到两个数，使得它们的和等于目标值，可以首先固定第一个数，然后寻找第二个数，第二个数等于目标值减去第一个数的差。利用数组的有序性质，可以通过二分查找的方法寻找第二个数。为了避免重复寻找，在寻找第二个数时，只在第一个数的右侧寻找。

参考代码

class Solution:def twoSum(self, numbers: List[int], target: int) -> List[int]:n = len(numbers)for i in range(n):low, high = i + 1, n - 1while low <= high:mid = (low + high) // 2if numbers[mid] == target - numbers[i]:return [i + 1, mid + 1]elif numbers[mid] > target - numbers[i]:high = mid - 1else:low = mid + 1return [-1, -1]

复杂度分析

• 时间复杂度：O(nlog⁡n)O(nlog⁡n)O(nlog⁡n)，其中 nnn 是数组的长度。需要遍历数组一次确定第一个数，时间复杂度是 O(n)O(n)O(n)，寻找第二个数使用二分查找，时间复杂度是 O(logn)O(logn)O(logn)，因此总时间复杂度是 O(nlogn)O(nlogn)O(nlogn)。
• 空间复杂度：O(1)O(1)O(1)。

2. 双指针

        思路参考自————一张图告诉你 O(n) 的双指针解法的本质原理

为什么双指针往中间移动时，不会漏掉某些情况呢？

        在这道题中，我们要寻找的是符合条件的一对下标 (i,j)(i, j)(i,j)，它们需要满足的约束条件是：

• i、j 都是合法的下标，即 0≤i
• i < j（题目要求）

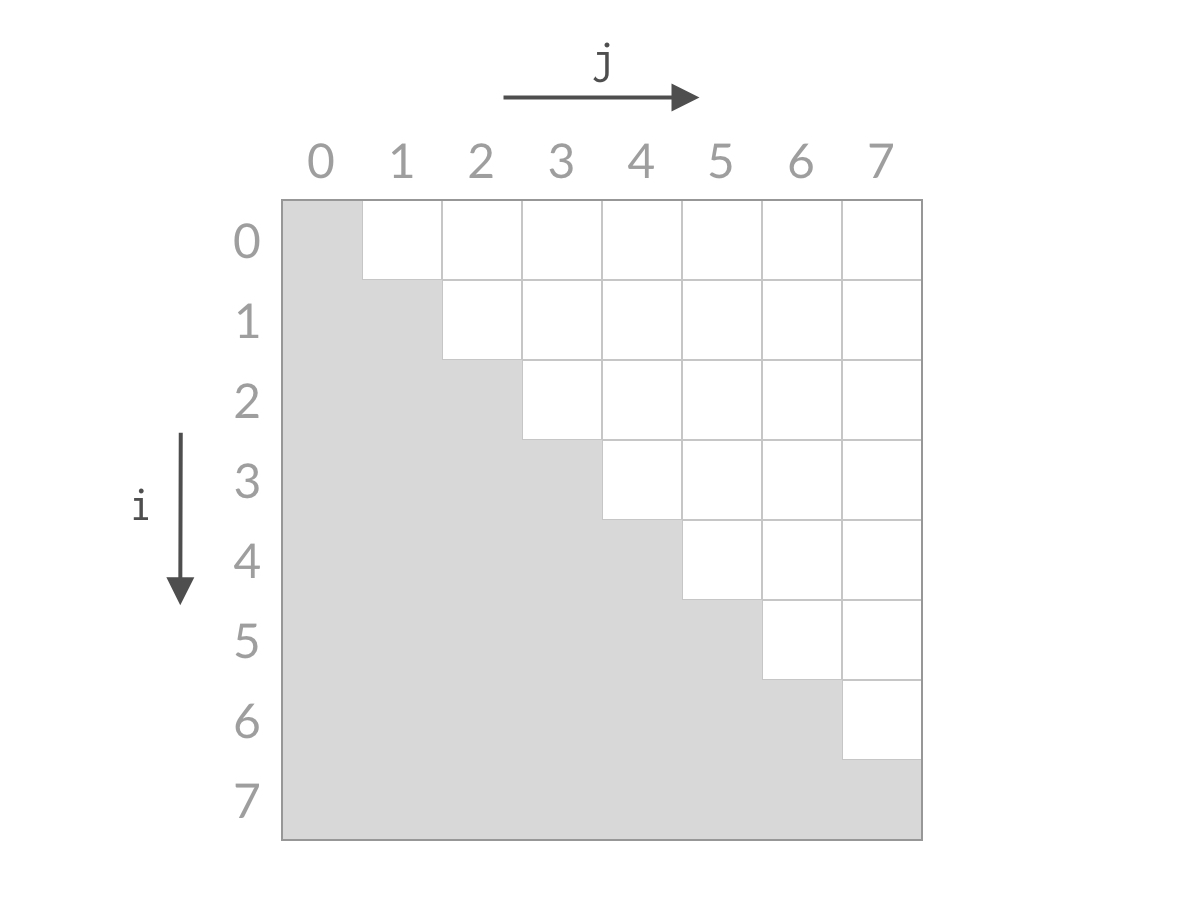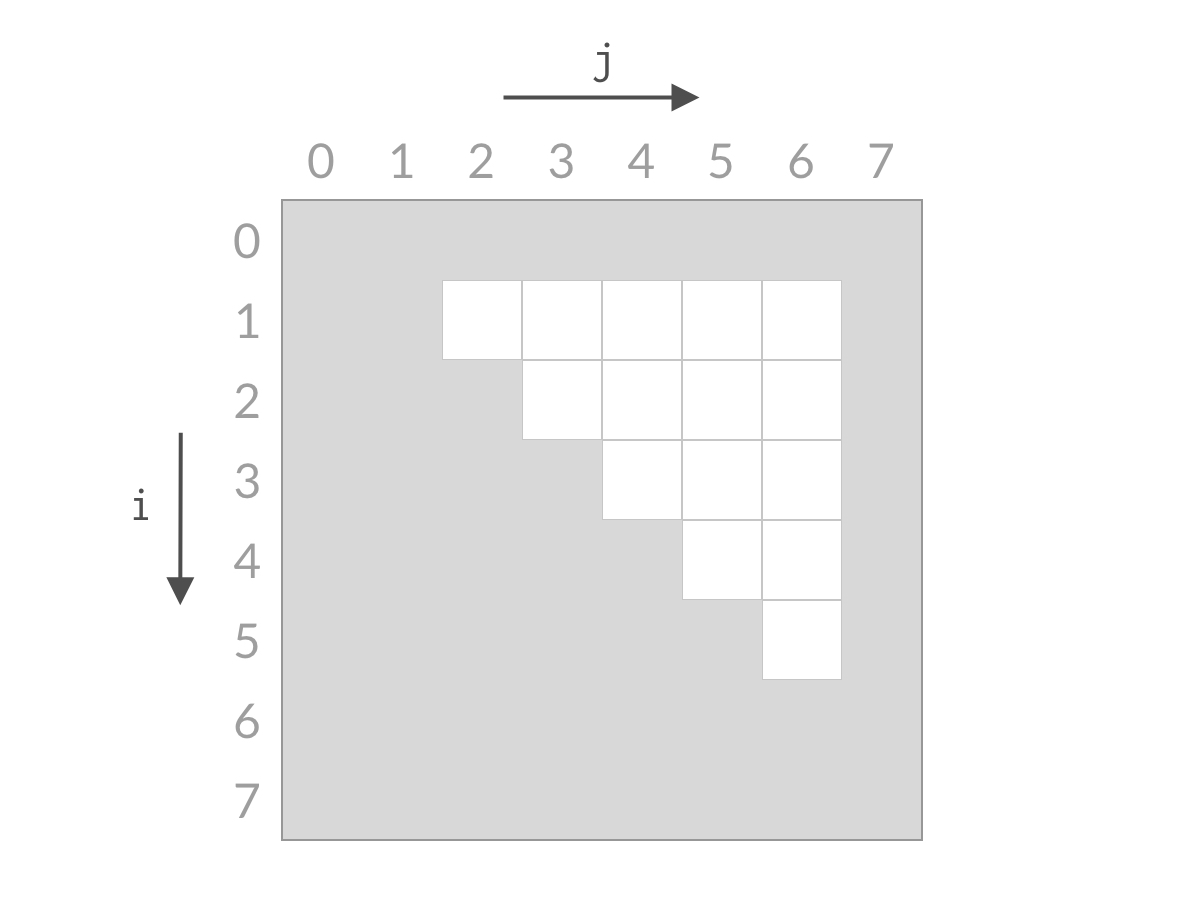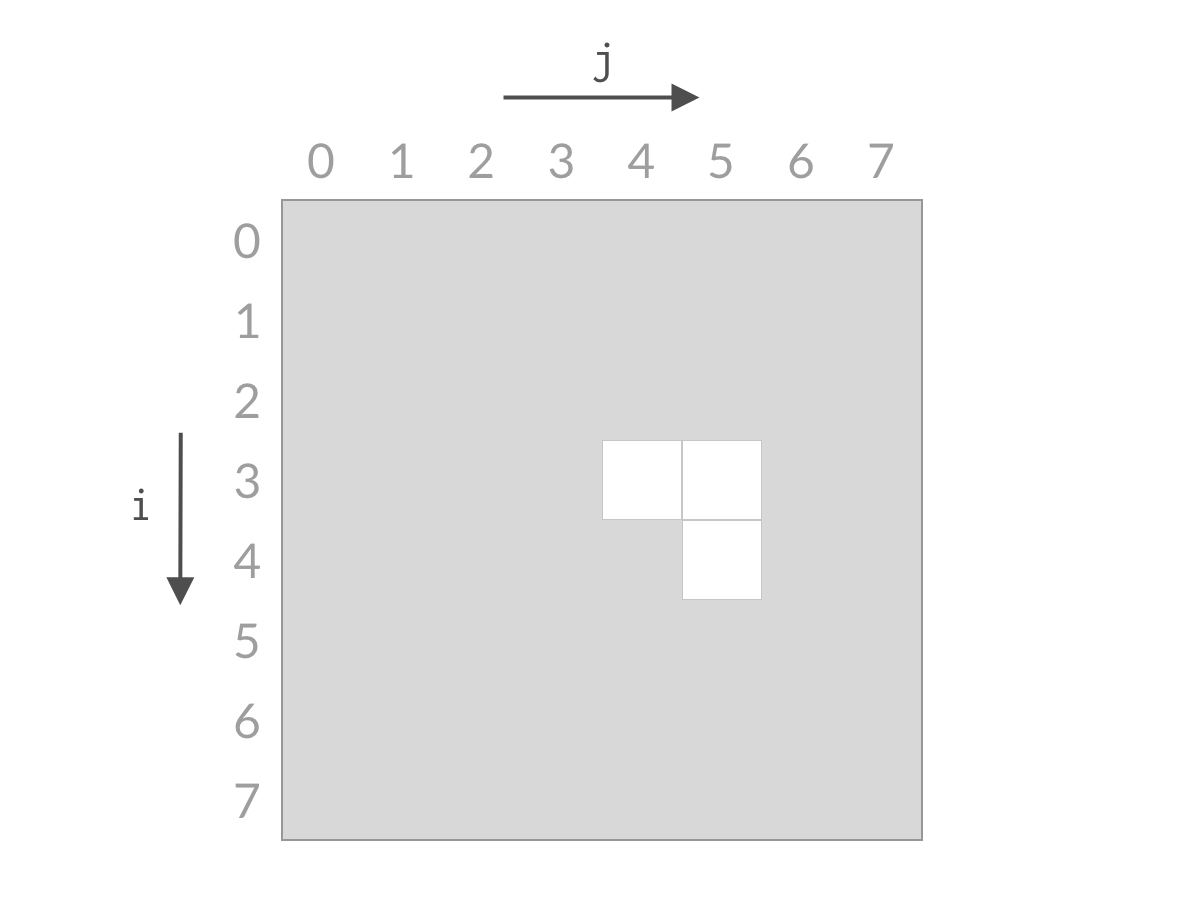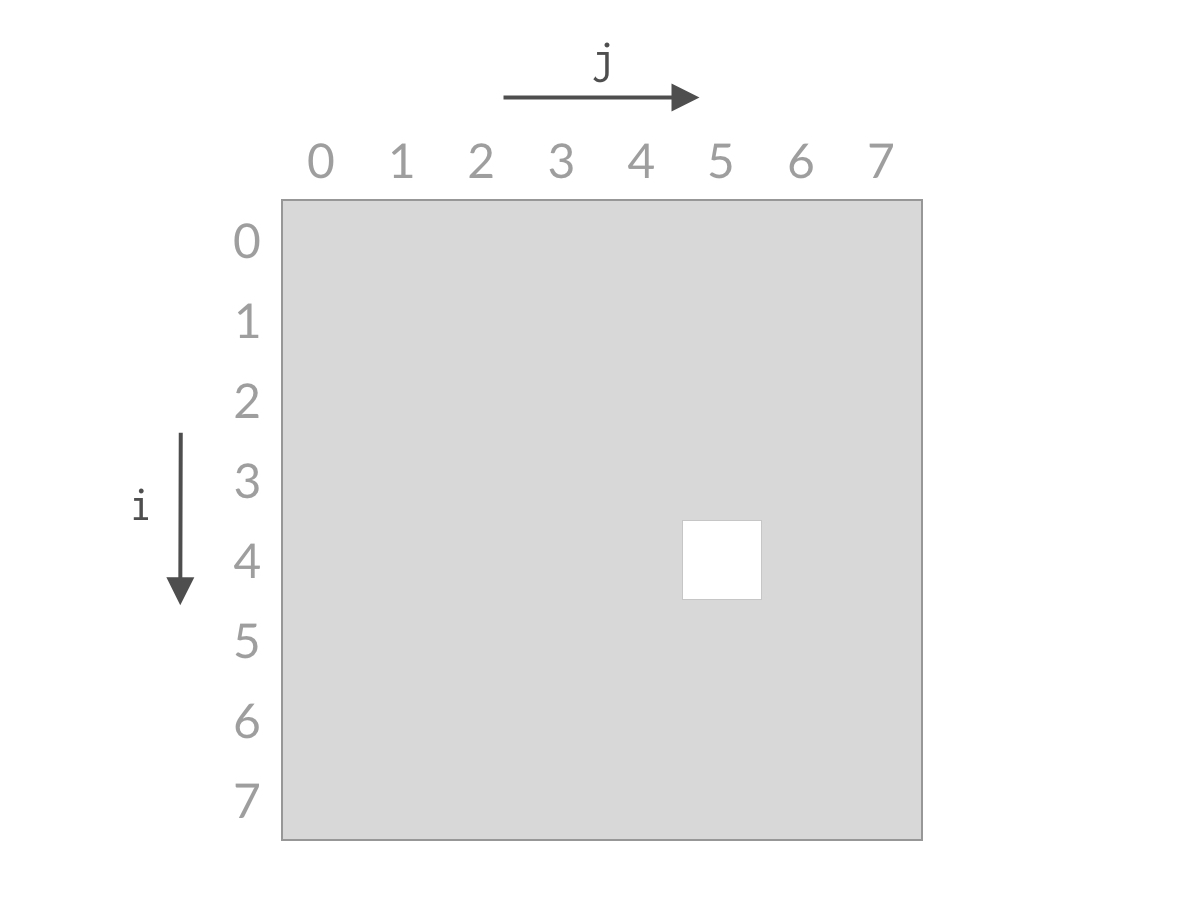
        而我们希望从中找到满足 A[i]+A[j]==targetA[i] + A[j] == targetA[i]+A[j]==target 的下标 (i,j)。以 n=8 为例，这时候全部的搜索空间是：

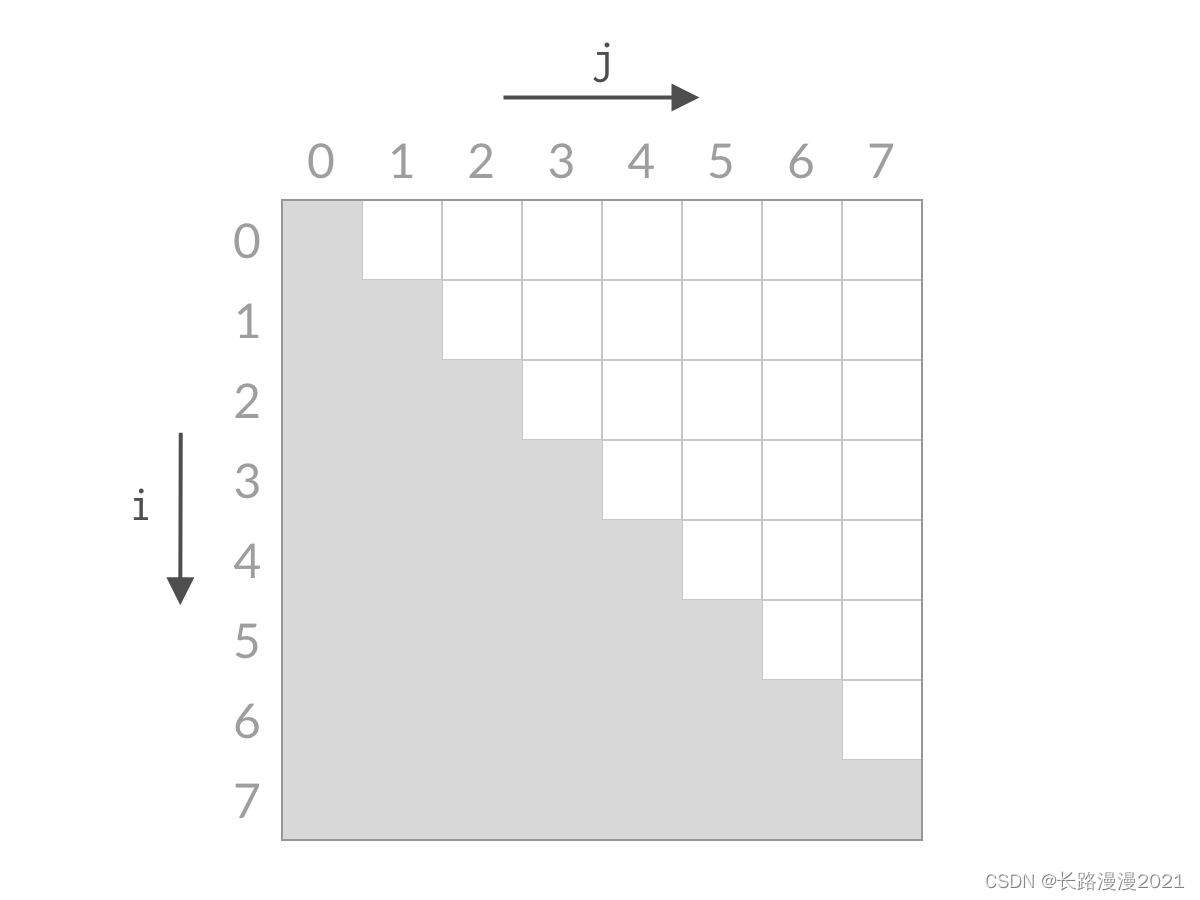
        由于 i、ji、ji、j 的约束条件的限制，搜索空间是白色的倒三角部分。可以看到，搜索空间的大小是 O(n2)O(n^2)O(n2) 数量级的。如果用暴力解法求解，一次只检查一个单元格，那么时间复杂度一定是 O(n2)O(n^2)O(n2)。要想得到 O(n)O(n)O(n) 的解法，我们就需要能够一次排除多个单元格。那么我们来看看，本题的双指针解法是如何削减搜索空间的：

        一开始，我们检查右上方单元格 (0,7)，即计算 A[0]+A[7]A[0] + A[7]A[0]+A[7]，与 target 进行比较。如果不相等的话，则要么大于 target，要么小于 target。

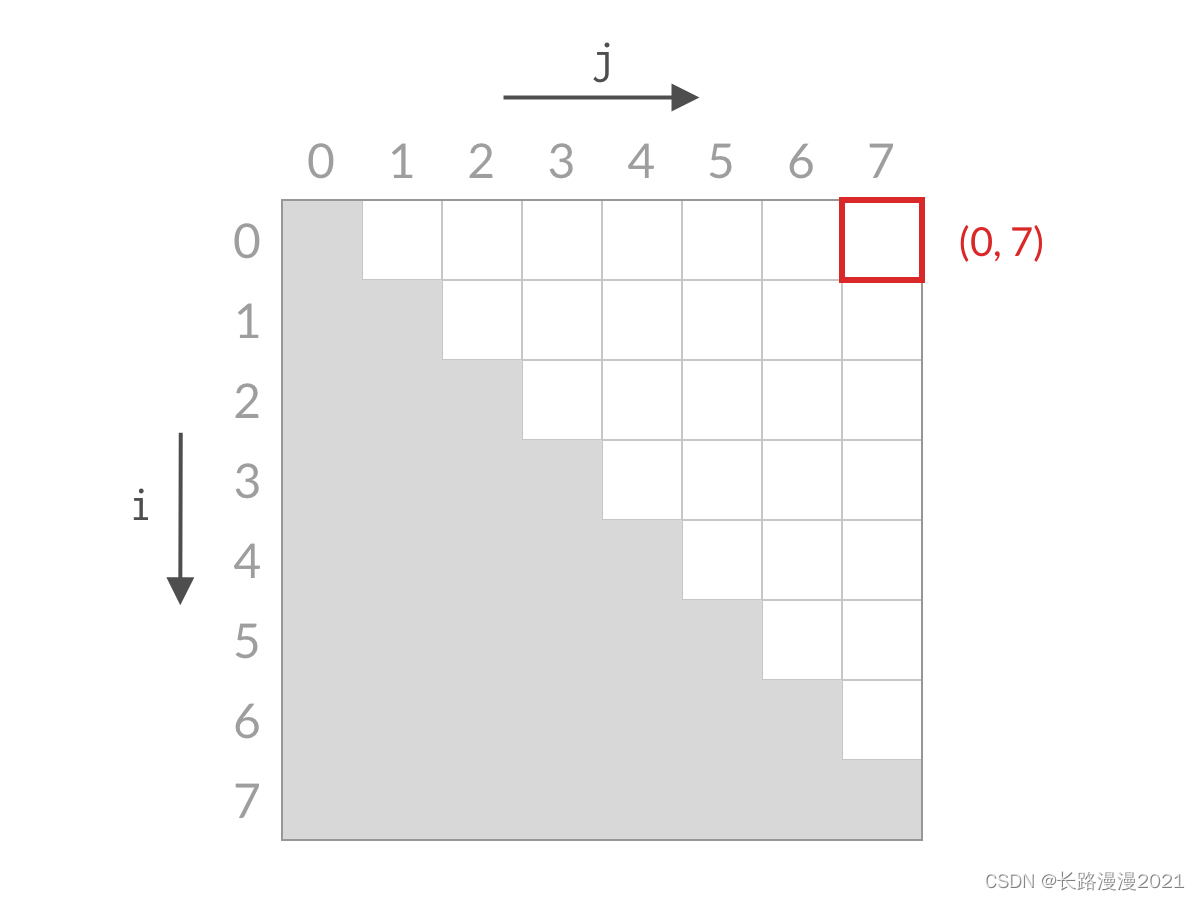
        假设此时 A[0]+A[7]A[0] + A[7]A[0]+A[7] 小于 target。这时候，我们应该去找和更大的两个数。由于 A[7] 已经是最大的数了，其他的数跟 A[0] 相加，和只会更小。也就是说 A[0]+A[6]、A[0]+A[5]、⋯、A[0]+A[1]A[0] + A[6] 、A[0] + A[5]、\cdots、A[0] + A[1]A[0]+A[6]、A[0]+A[5]、⋯、A[0]+A[1] 也都小于 target，这些都是不合要求的解，可以一次排除。这相当于 i=0i=0i=0 的情况全部被排除。对应用双指针解法的代码，就是 i++i++i++，对应于搜索空间，就是削减了一行的搜索空间，如下图所示。

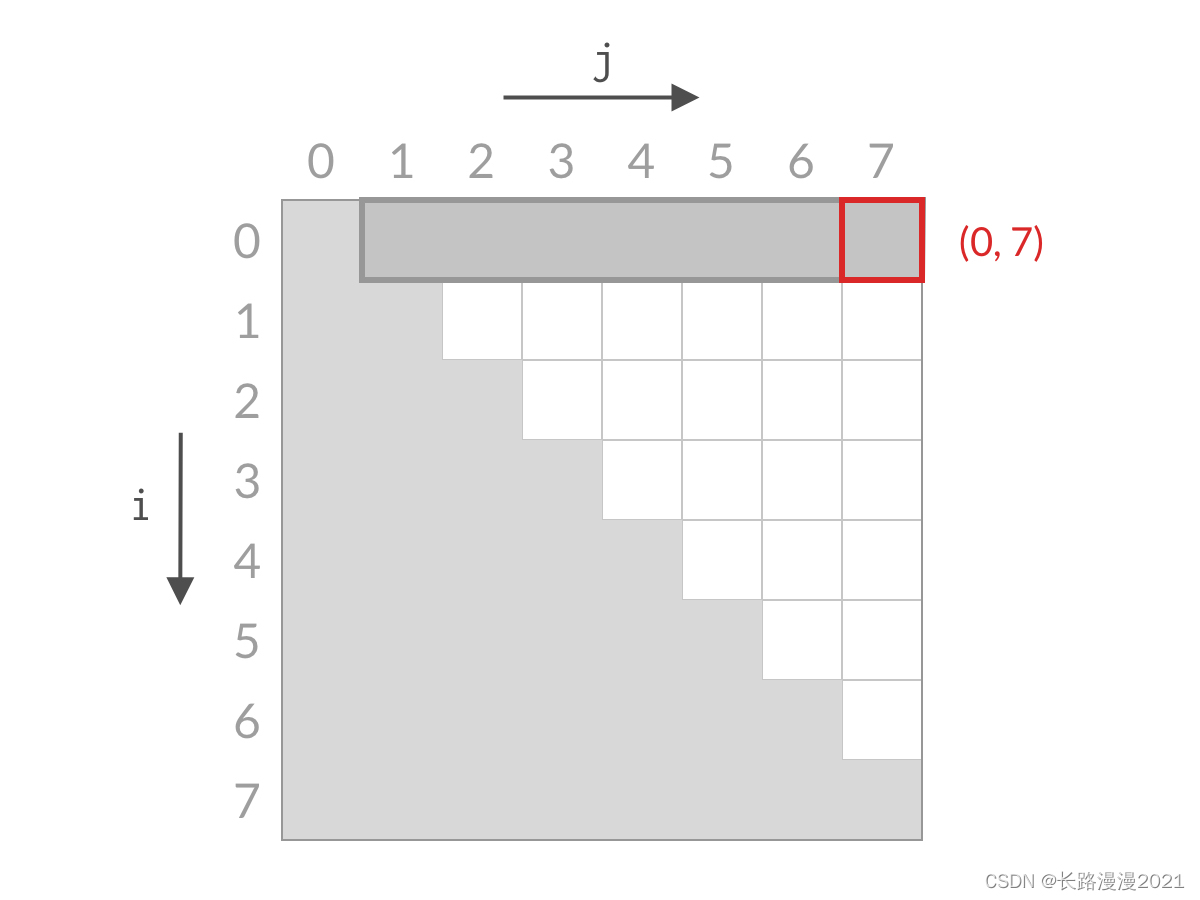
        排除掉了搜索空间中的一行之后，我们再看剩余的搜索空间，仍然是倒三角形状。我们检查右上方的单元格 (1,7)(1,7)(1,7)，计算 A[1]+A[7]A[1] + A[7]A[1]+A[7] 与 target 进行比较。

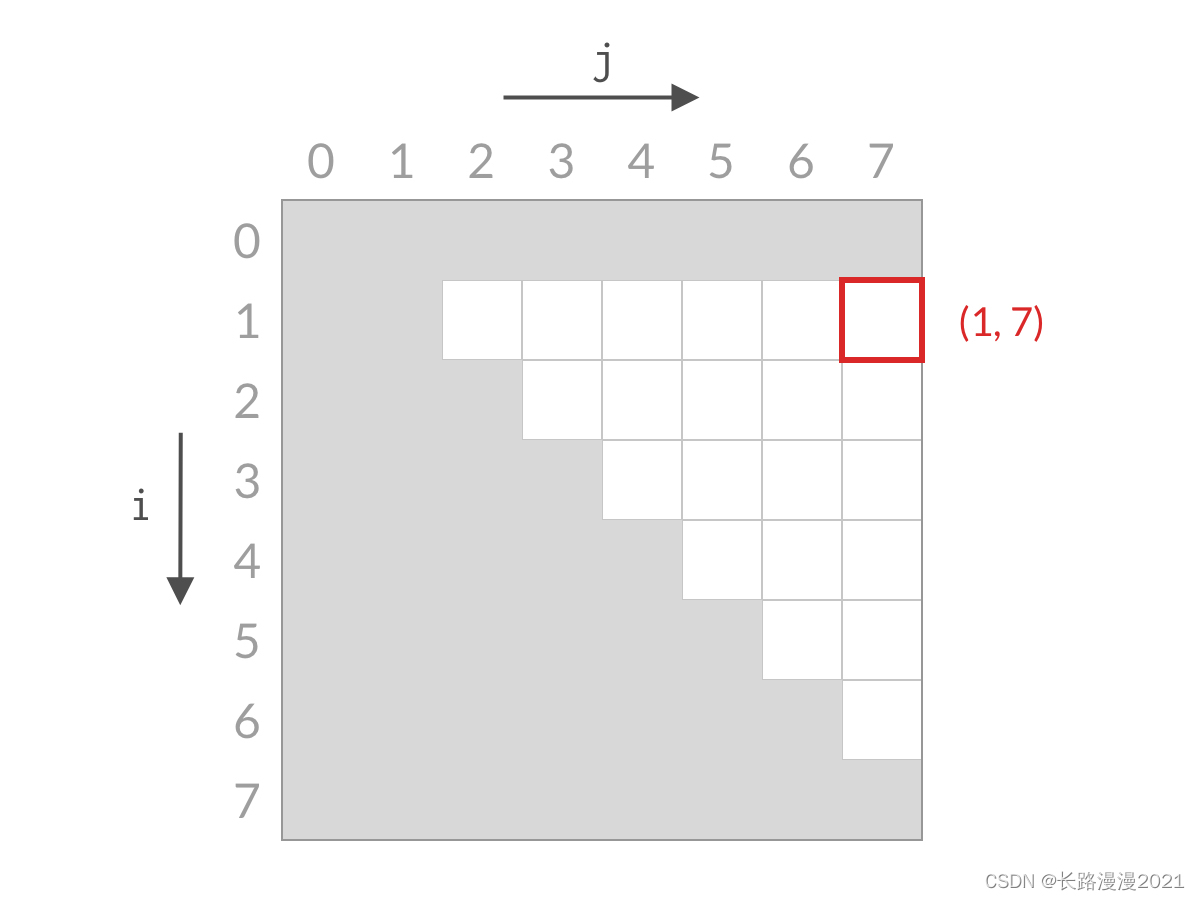
        假设此时 A[0]+A[7]A[0] + A[7]A[0]+A[7] 大于 target。这时候，我们应该去找 和更小的两个数。由于 A[1] 已经是当前搜索空间最小的数了，其他的数跟 A[7] 相加的话，和只会更大。也就是说 A[1]+A[7]、A[2]+A[7]、⋯、A[6]+A[7]A[1] + A[7] 、A[2] + A[7]、\cdots、A[6] + A[7]A[1]+A[7]、A[2]+A[7]、⋯、A[6]+A[7] 也都大于 target，这些都是不合要求的解，可以一次排除。这相当于 j=0j=0j=0 的情况全部被排除。对应用双指针解法的代码，就是 j++j++j++，对应于搜索空间，就是削减了一列的搜索空间，如下图所示。

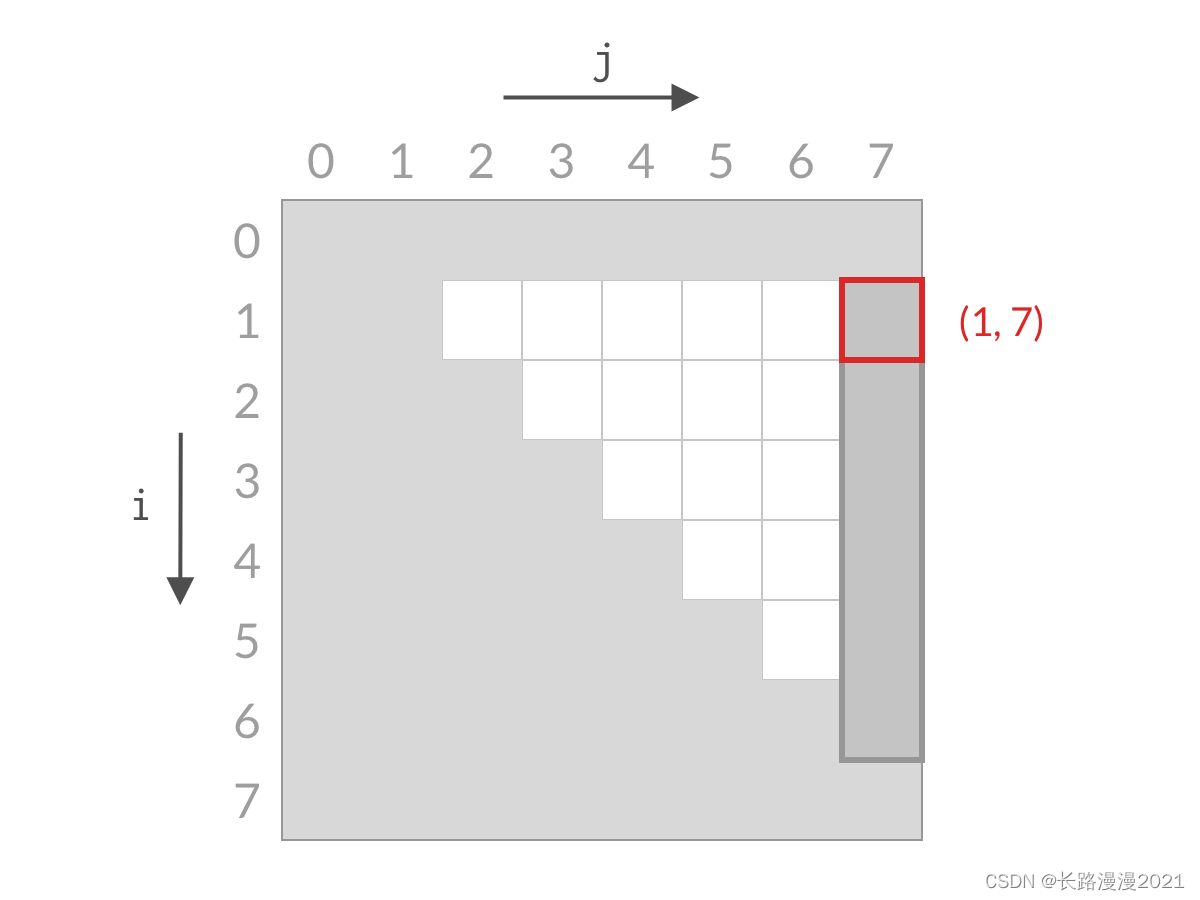
        可以看到，无论 A[i]+A[j]A[i] + A[j]A[i]+A[j] 的结果是大了还是小了，我们都可以排除掉一行或者一列的搜索空间。经过 nnn 步以后，就能排除所有的搜索空间，检查完所有的可能性。搜索空间的减小过程如下面动图所示：

参考代码

class Solution:def twoSum(self, numbers: List[int], target: int) -> List[int]:head, tail = 0, len(numbers)-1while head < tail:two_sum = numbers[head] + numbers[tail]if two_sum == target:return [head+1, tail+1]elif two_sum > target:tail -= 1else:head += 1

复杂度分析

• 时间复杂度：O(n)O(n)O(n)，其中 nnn 是数组的长度。两个指针移动的总次数最多为 nnn 次。
• 空间复杂度：O(1)O(1)O(1)。