文章目录

• 0. 参考资料
• 1. Intro Example 例子引入
• • 1.1. 测量硬币直径
  • 1.2. 思考
• 2. Data Fusion 数据融合
• • 2.1. 数据融合在做什么？
  • 2.2. 数据融合的前提——不确定度
  • 2.3. 数据融合的结果——统计意义下的最优估计
• 3. State Space Representation 状态空间表达式
• • 3.1. 状态方程
  • 3.2. 观测方程
  • 3.3. 系统状态空间方程举例
• 4. Kalman Filter 卡尔曼滤波
• • 4.1. Kalman Filter 在做什么？
  • 4.2. Kalman Filter 的思路
  • 4.3. Kalman Gain
  • 4.4. Kalman Filter 五大公式总结

0. 参考资料

【卡尔曼滤波器】_Kalman Filter_全网最详细数学推导

1. Intro Example 例子引入

1.1. 测量硬币直径

给你如下不同的传感器，如何得到硬币的直径？

• Test 1：只给你一个米尺。
  Answer 1：用米尺测两次硬币直径，取平均值。

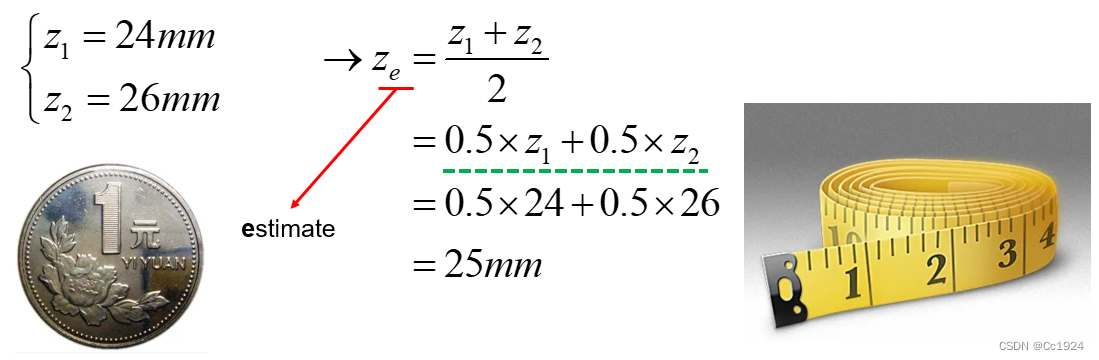
• Test 2：给你两个刻度分辨率不同的米尺。
  Answer 2：分别用两个米尺测量一次，此时还能取平均值吗？
  

• Test 3：给你一个米尺和一个千分尺。
  Answer 3：分别用米尺和千分尺各测量一次，此时还能取平均值吗？
  

1.2. 思考

显然随着传感器精度的不同，我们使用不同的传感器测量的结果不能再简单的取平均值了，因为在不考虑系统误差的情况下，千分尺的测量结果显然要比米尺的测量结果更准确。

那么如何从不同传感器的测量结果中，得到我们对硬币直径的最优估计？这就需要后面数据融合的方法！

2. Data Fusion 数据融合

2.1. 数据融合在做什么？

使用不同的传感器，获得对系统状态的最优估计。

比如上述例子中，使用不同的传感器测量硬币直径，最后需要给出对硬币直径的最优估计。

2.2. 数据融合的前提——不确定度

没有完全准确的传感器，也不存在完全准确的测量过程。也就是说，每次测量都是存在不确定度的，只不过是在不考虑系统误差的情况下，传感器精度越高，其测量的不确定度就越小。比如上述例子中，千分尺的测量不确定度就要远小于米尺的测量不确定度。

不确定度在统计学中就是标注差、方差、协方差矩阵的概念。显然在前面的例子中，在对不同传感器测量的结果进行加权平均的时候，我们应该考虑不同传感器的不确定度，也就是不确定度越小的传感器，其测量值所占的权重应该越大，因为它更准确。

2.3. 数据融合的结果——统计意义下的最优估计

每次测量都是有不确定度的，所以从统计意义上讲我们的测量值是一个随机变量，而最终我们对系统状态的估计值也是一个随机变量。那么最优的数据融合结果应该有最小的方差，对于多维随机变量来说就是拥有最小的协方差矩阵的迹。

所以下面我们推导前面的不同传感器测量的结果进行加权平均的时候，目的就是让最后加权平均的结果有最小的方差。

推导结果如上图所示，其中两侧测量是独立的，所以根据方差的性质可以展开成两部分。然后最终的目的是求解kkk让方差最小，所以我们就是对kkk求导，导数为0的点就是极值点。

最终的结果也是容易解释的，分成两种情况：

• σ12\sigma_1^2σ12​非常大，kkk趋向1，融合结果趋向z2z_2z2​。这个显然是对的，因为测量1的方差很大，也就是它的测量结果更不准确，所以我们倾向于相信测量2的结果。
• σ22\sigma_2^2σ22​非常大，kkk趋向0，融合结果趋向z1z_1z1​。分析同上。

利用我们上面推导得到的公式，带到前面米尺和千分尺测量硬币直径的例子中，看一下最终融合的结果，可以发现结果非常靠近千分尺的结果，这个也是我们想要的。

3. State Space Representation 状态空间表达式

在机器人状态估计问题中，并不是简单的两个传感器测量状态然后融合结果的过程，而是通常会对系统的运动过程做一个建模，根据这个建模的运动过程我们就可以预测系统的状态。当有新的传感器测量之后，再根据测量结果更新我们对系统状态的预测值，从而达到更优的系统状态估计。

上述过程其实就是系统的状态空间表达式，在Kalman Fiter中分为状态方程和观测方程两个部分：

3.1. 状态方程

对系统的物理模型进行数学建模，比如SLAM中假设机器人在做匀速匀速或者加速运动，那么建立的数学模型就分别是匀速运动模型和加速运动模型。

总而言之，状态方程是我们算出来的，或者推导出来的。知道了系统上一时刻的状态，利用状态方程，我们就可以计算得到当前时刻的系统状态，这就是对系统状态的预测。

另外一个值得注意的问题是，和 数据融合 章节中我们提到的一样，不管是测量值还是我们这里的数学建模，都是有不确定性的，比如这里我们建立的数学模型可能不准确，所以状态方程是有噪声的。在Kalman Filter中，假设噪声符合高斯分布，这是后面推导Kalman Gain的必要前提条件。

3.2. 观测方程

这个和前面测量硬币直径是一样的，就是我们对系统状态进行的观测。但是在SLAM中可能没有前面那么直接，而是有一个观测模型在里面。比如VIO中我们要估计系统的6DOF位姿，但是其实我们从相机中直接拿到的是特征点观测的像素值，而不是直接对系统6DOF的观测值。但是这个观测值和系统的6DOF状态是有关系的，也就是相机的投影模型，在这个投影模型中，就把实际的 观测像素值 和 系统6DOF状态值 关联到一起了，这个关联的关系就是观测模型。

总而言之，观测方程尽管没有直接对要估计的系统状态进行测量，但是它通过观测模型间接对系统状态进行了测量，因此它最终还是对系统状态的测量。

同理，观测也是有噪声的，比如相机观测的特征点的位置可能并不是很准确，相机的投影模型可能也不是很准确，所以这里也要加入高斯噪声，注意这里也必须是高斯噪声，因为这是后面推导Kalman Gain的前提条件。

3.3. 系统状态空间方程举例

假设有个小车，上面有一个单线激光发射器可以测量它离起始点的距离，有一个轮速计可以测量轮子的速度。现在我们的目的就是估计这个小车的状态，那么系统状态空间方程可以建立如下：

注意：上述建立状态空间方程的过程中，把轮速计的测量加到了状态方程中，把激光的测量加到了观测方程中。按理说他俩不都是观测吗？为什么要把轮速计加到状态方程中呢？

其实把轮速计加到观测方程中和加到状态方程中本质是一样的，加到状态方程中我们就把噪声加到了轮速的地方，这个时候它就是作为状态方程的输入量uuu。如果把它加到观测方程中，那么状态方程中uuu就是0了，系统就是靠上次的速度递推这次的状态，然后轮速计在观测方程中对速度进行约束。可以发现其实这两种建模方式都是本质是一样的，只不过是在数学表达上不太一样。

4. Kalman Filter 卡尔曼滤波

4.1. Kalman Filter 在做什么？

Kalman Filter（卡尔曼滤波），名字叫做滤波，但是更准确的说它不是一个滤波器，而是一个状态估计器。

它的目的就是利用系统的状态方程和观测方程，得到对系统状态在统计意义下的最优估计。

注意：Kalman Filter的两大前提：

• 状态方程和观测方程都是线性的，也就是要有系数矩阵AAA和HHH；
• 状态方程和观测方程的噪声都是高斯噪声。

注意这两个条件是卡尔曼滤波应用的前提条件，因为只有在这两个前提条件下，推导得到的 Kalman Gain 才能让融合的结果在统计意义上是最优的。

4.2. Kalman Filter 的思路

既然是用状态方程和观测方程融合，那么就写出来他们对系统状态的估计结果，然后像测量硬币直径一样对两个结果进行数据融合就可以了。如下所示：

注意：

• 用状态方程得到的结果称为预测值，其中在计算的过程中我们把过程噪声www认为是0，因为它是0均值的高斯分布 。这个噪声这次到底是多少我们没办法知道，因为它是随机的高斯噪声。如果知道了我们就不用做Kalman Filter了，直接把噪声的值带入状态空间方程中，就得到系统的真值状态了。正是因为我们不知道每一次噪声到底是多少，才需要用Kalman Filter来估计系统的状态。所以我们在计算的时候，只能把噪声值设置成它的均值，也就是0。当前如果噪声的均值不是0，那么是多少这里带入多少就行了，总之带入的就是噪声www的均值。观测方程中对噪声的处理同理。
• 观测方程中，由于它不是直接对系统状态进行观测，而是有一个观测模型。也就是有一个系数矩阵HHH在系统状态变量和观测变量之间做了映射，因此我们想要从传感器测量中得到直接对状态的观测，需要求伪逆。这个地方只是为了后续推导的理解方便，最终Kalman Filter的结果中是不存在这个求伪逆的过程的。

套用数据融合的思路，我们只需要对状态预测值和状态观测值做加权就可以了，如下所示：

对前面的加权平均的式子进行进一步推导，消掉其中求HHH的伪逆的过程，可以得到如下结果，其中的KKK就是大名鼎鼎的 Kalman Gain：

在套用数据融合中的思路，我们最终的目的就是找到一个合适的权重系数，让最终的加权平均的结果有最小的方差，对于多维随机变量来说就是有最小的协方差矩阵的迹。如下所示：

注意：

• 其中预测状态的协方差P^k\hat{P}_kP^k​是通过系统的状态方程计算出来的。而观测方程的协方差因为现在我们没有从观测空间转到状态空间，也就是没有求伪逆，所以直接就是观测的协方差RRR。

4.3. Kalman Gain

这个部分非常复杂，详细的推导过程可以参照B站视频：【卡尔曼滤波器】3_卡尔曼增益超详细数学推导 ～全网最完整

或者我的手写笔记：Kalman Filter in SLAM (1.5) ——Derivation of Kalman Gain and Covariance Matrix (卡尔曼增益和协方差矩阵推导)

这里直接给出结果：

4.4. Kalman Filter 五大公式总结

• 状态方程做预测：根据上一时刻的状态和系统状态空间方程，对当前时刻的状态做预测，同时会更新当前预测的状态的协方差矩阵：

• 观测方程做更新：首先计算 Kalman Gain，然后把它当做权重融合预测状态和观测值，得到系统的最优估计。可以看到，这里预测值是系统状态，观测值是传感器直接的观测量，所以 Kalman Gain 是有量纲的，而且它的量纲和H−1H^{-1}H−1量纲是一样的。