一、朴素贝叶斯引入

​ 我们所处在的这个世界是充满概率的一个世界。甚至可以说，世界上所有事情的发生都是有一定概率的，并不存在绝对发生与绝对不发生。

​ 比如，你同桌他高考考得分数比你高，他未来工作薪资比你高只是一个可能性事件，在大部分人的认知里，“他未来工作薪资比你高”这个是个大概率事件；但是在我的认知里，绝不是这么一回事。没准他去了他梦想中的天坑专业出来工作都找不到，而你去了一个就业前景好的专业，那么之前那个结论他就不成立。

​ 再比如，我们进入大学后身边会存在很多“认真学习的人”，他们不仅像高中一样上早自习和晚自习，而且会将书上的例题和课后习题刷三遍。如果此时我们想根据你一个室友是否上早自习和晚自习、是否刷书上习题三遍这两个特点来推断他是否有保研名额，那么我们会先根据之前学长学姐的经验来判断。假设我们就有这么一个学长，他上早自习也上晚自习，但是只将书上的题刷一遍，最后取得了保研名额，那么此时你就会认为，你那位既上早自习也上晚自习又将书上的题刷三遍的室友很有可能能够保研。是“很有可能”，但并不是“一定”。如果此时我们还有另外一个学长，他上早自习也上晚自习，并且将书上的题刷三遍，但是他并没有保研，那么这时候你会对你室友能够保研的相信程度降低。如果按照决策树算法，你室友会被分类到不能保研一类。如果你使用支持向量机SVM算法，你室友还是有可能被分类到保研一类。但事实上，此时更能贴切描述你室友保研与否的并不是到底能不能保研这一个确定值，而是一个能够保研或者无法保研的一个概率值。这种概率的预测是无法用决策树或者SVM能够解决的，而我们今天要介绍的一个算法——朴素贝叶斯算法，是能够进行解决的。

​ 朴素贝叶斯算法所得到的结果并不是一个确定的值，是与否，而是一个概率：是的概率还是否的概率。

二、朴素贝叶斯预备知识

概念引入

• 条件概率：

生活中很多概率都是在某些特殊条件下的概率。比如你想知道你在家感染新冠的概率，这是取决于很多方面的，比如，政策有没有放开、是否位于高风险区等等。只有在这些条件的限制下，我们才能较为准确的求出你想知道的概率。

在一个事件发生的条件下，发生另外一个事件的概率。事件A在事件B的条件下发生的概率写作P(B∣A)P(B|A)P(B∣A)。条件概率的计算公式如下：
P(A∣B)=P(AB)P(B)P(A|B)=\frac{P(AB)}{P(B)} P(A∣B)=P(B)P(AB)​
韦恩图理解：

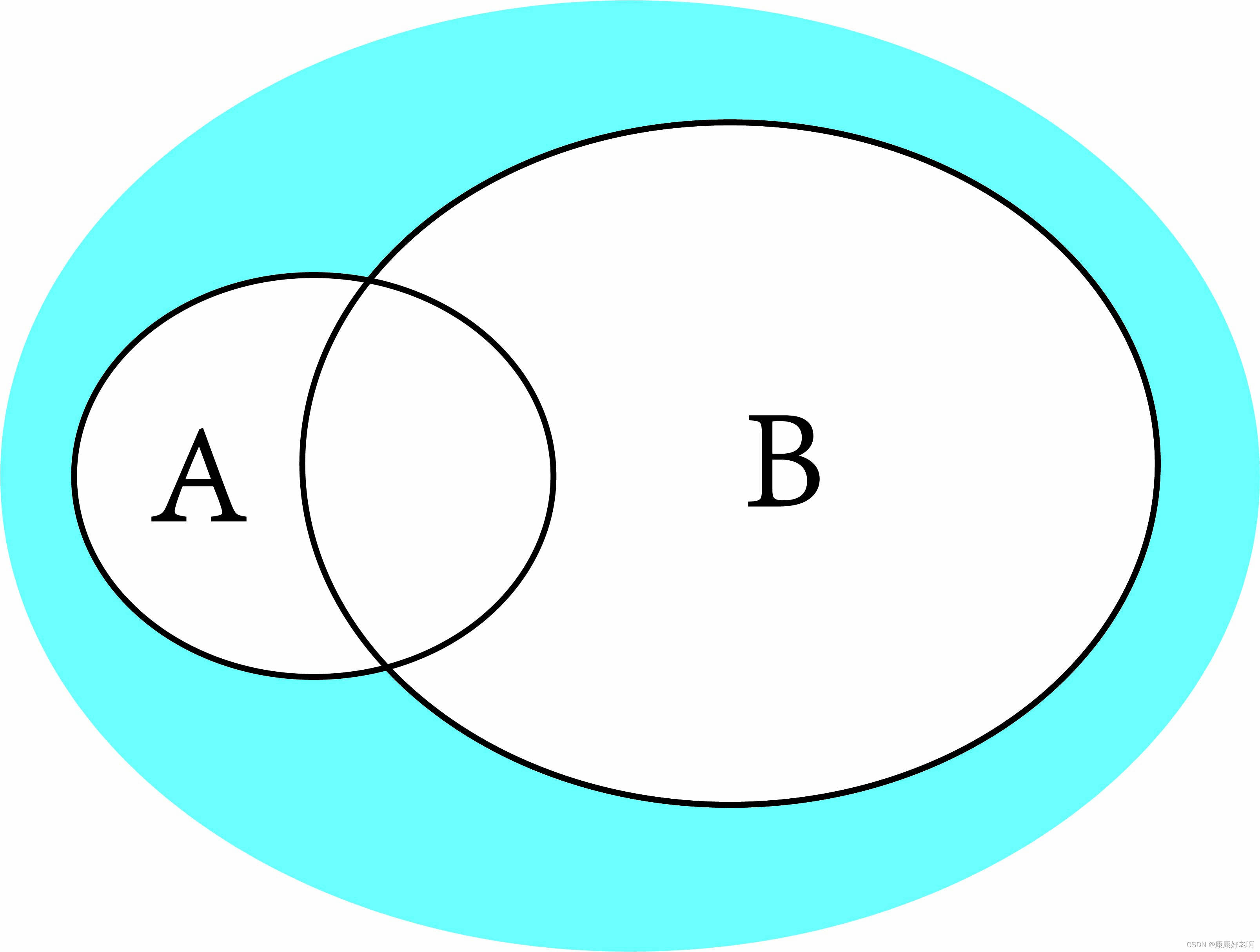
上面A、B分别有两个椭圆，代表了他们的事件范围。我们想要求在B的条件下A发生的概率，那么直观上分母应该是P(B)，因为条件是事件B就相当于要以事件B作为基础；而由于事件B的限制，事件A中不属于B的部分应该被舍去，它们不在B的控制之下。所以也很容易理解，分子是A和B的和事件（交集）的概率。

• 先验概率：事件发生前预判的概率。即在事件发生前根据之前的经验判断事件发生的概率。对应的是上面公式的P(A)P(A)P(A)。

• 后验概率：事件发生后反向条件概率。即事件已经发生了，在事件发生的这个条件之下，发生某个事件的概率。对应的是上面公式的P(B∣A)P(B|A)P(B∣A)，即事件A已经发生后，反推事件B发生的概率。

比如，我们知道成为新冠阳性密接者可能会导致自己变成阳性。我们可以求在成为密接的条件下自己变阳的概率，这就是条件概率。我们也可以在知道自己阳了之后求我们是密接的概率，这个就是后验概率，因为我们知道了结果反推原因。

• 朴素：在朴素贝叶斯中，“朴素”的意思是假设所有输入事件之间是相互独立的。在这样假设之后，独立事件间的概率会更加简单。

乘法公式

在上文我们知道条件概率的公式为：P(A∣B)=P(AB)P(B)P(A|B)=\frac{P(AB)}{P(B)}P(A∣B)=P(B)P(AB)​。那如果我们此时知道P(B)和P(A|B)，相求P(AB)，可以通过移项转化成下列公式：
P(A∣B)P(B)=P(AB)P(A|B)P(B)=P(AB) P(A∣B)P(B)=P(AB)
同理，我们也可以得到：

P(B∣A)P(A)=P(AB)P(B|A)P(A)=P(AB) P(B∣A)P(A)=P(AB)
这两个公式我们称其为乘法公式。上面两个式子在实际计算中要根据问题灵活选择。

我们也可以将其拓展到n个事件中：
P(A1A2…An)=P(A1)P(A2∣A1)P(A3∣A2A1)…P(An∣An…A2A1)P(A_1A_2…A_n)=P(A_1)P(A_2|A_1)P(A_3|A_2A_1)…P(A_n|A_n…A_2A_1) P(A1​A2​…An​)=P(A1​)P(A2​∣A1​)P(A3​∣A2​A1​)…P(An​∣An​…A2​A1​)

我们可以这样理解：P(A1)P(A_1)P(A1​)是假设A1正确，P(A2∣A1)P(A_2|A_1)P(A2​∣A1​)是假设A1正确的情况下A2正确，以此类推。由于生活中几乎所有事件都是条件概率，即在某种条件下发生的概率，而条件有可能层层嵌套，所以才有了乘法公式。

全概率公式

有限划分

基本概念：设Ω\OmegaΩ为随机试验E的样本空间，B₁，B₂ ，…，B_n为E的一组事件，若

(1) Bi∩Bj=f,i≠jBi∩Bj =f ,i ≠ jBi∩Bj=f,i=j

(2) B1∪B2∪…∪Bn=ΩB_1∪B_2 ∪… ∪B_n=\OmegaB1​∪B2​∪…∪Bn​=Ω

则称B₁，B₂，…，B_n 为∅\emptyset∅的一个有限划分，或称完备事件组。

注：样本空间的划分不唯一

简单理解下，有限划分的意思就是，将一个样本空间切成许多小份。

全概率公式

基本概念：设A为随机试验E的样本空间，B₁，B₂ ，…，B_n为E的一个有限划分，且P(B_i)＞0，则
P(A)=∑i−1nP(Bi)P(A∣Bi)P(A)=\sum_{i-1}^nP(B_i)P(A|B_i) P(A)=i−1∑n​P(Bi​)P(A∣Bi​)

其实这就是乘法原理的加强版，将很多个乘法原理结合起来使用

总结一下，其实全概率公式就是加法公式，将不同条件下的概率利用加法结合起来；乘法原理就是乘法公式，当出现连环条件时利用乘法结合起来

贝叶斯公式

概念引入

先验概率：事件发生前预判的概率。即在事件发生前根据之前的经验判断事件发生的概率。对应的是上面公式的P(A)P(A)P(A)。

后验概率：事件发生后反向条件概率。即事件已经发生了，在事件发生的这个条件之下，发生某个事件的概率。对应的是上面公式的P(A∣B)P(A|B)P(A∣B)，即事件B已经发生后，事件A发生的概率。

从我们日常生活中的理解不难发现，后验概率受到先验概率的影响很大。

贝叶斯公式

设Ω\OmegaΩ为随机试验E的样本空间，B₁，B₂ ，…，B_n为E的一个有限划分，A⊂Ω\subset\Omega⊂Ω，且P(A)>0，P(B_i)>0，则：
P(Bi∣A)=P(Bi)P(A∣Bi)∑j=1nP(Bj)P(A∣Bj)P(B_i|A)=\frac{P(B_i)P(A|B_i)}{\sum_{j=1}^nP(B_j)P(A|B_j)} P(Bi​∣A)=∑j=1n​P(Bj​)P(A∣Bj​)P(Bi​)P(A∣Bi​)​
简单推导：
P(Bi∣A)=P(ABi)P(A)=P(Bi)P(A∣Bi)∑j=1nP(Bj)P(A∣Bj)P(B_i|A)=\frac{P(AB_i)}{P(A)}=\frac{P(B_i)P(A|B_i)}{\sum_{j=1}^nP(B_j)P(A|B_j)} P(Bi​∣A)=P(A)P(ABi​)​=∑j=1n​P(Bj​)P(A∣Bj​)P(Bi​)P(A∣Bi​)​
分子分母分别使用乘法公式和全概率公式。

P(B|A)是后验概率，P(A|B)是先验概率。

通过贝叶斯公式，我们可以在事件A发生后（即为条件）求发生事件B_i的概率，其中事件B_i是促使事件A发展的一部分。下面举一个十分经典的例子：

假设一个病的发病率是0.0004（即2500人当中才有一个人得了这种病），现在有个可能得了该病的患者需要去医院进行检查。但是，医生检查并不会100%正确，多少会出现失误。已知该医院对该病患者判断没病的概率为1%，对没有该病患者判断有病的概率为0.1%。现在他通过检查发现得了该病，那请问他真正患病的概率有多少？

我们假设A={人是患者}，B={人检验有病}

通过对题目的分析，我们可以得到以下条件：

人群中得该病的概率为P(A)=0.0004,人群中得该病的概率为P(A)=0.0004,人群中得该病的概率为P(A)=0.0004,

人群中未得该病的概率为P(A‾)=09996,人群中未得该病的概率为P(\overline{A})=09996,人群中未得该病的概率为P(A)=09996,

人有病检验出来患病的概率为P(B∣A)=0.99,人有病检验出来患病的概率为P(B|A)=0.99,人有病检验出来患病的概率为P(B∣A)=0.99,

人没有病检验出来患病的概率为P(B∣A‾)=0.001人没有病检验出来患病的概率为P(B|\overline{A})=0.001人没有病检验出来患病的概率为P(B∣A)=0.001

那么我们要求的检验有病，真正患病的概率为：
P(A∣B)=P(AB)P(B)=0.0004×0.990.0013956=0.284P(A|B)=\frac{P(AB)}{P(B)}=\frac{0.0004×0.99}{0.0013956}=0.284 P(A∣B)=P(B)P(AB)​=0.00139560.0004×0.99​=0.284
这个概率是让人震惊的。医院给我检查出有病，但是我实际上只有四分之一左右的概率真正患病！

那么这是为什么呢？我们具体化一下数字：

假设现在有10000人。那么理论上不得病的人有9996人，而得病的只有4人。由于对正常人判断失误率为0.1%，那么约有10个没有得该病的人得了该病。而将患病的误判为没得病的概率为1%，4人中近似没有人会被判成没病。这样就很清楚了，因为没得病的人基数太高，所以哪怕误判的概率很低，相比于得病的人来说，其人数依然很高。

二、朴素贝叶斯

基础原理

​ 朴素贝叶斯，就是在“朴素”的假设下，使用贝叶斯公式。前文也提到，朴素贝叶斯就是假设各个事件（属性）相互独立的情况下使用贝叶斯公式。

为什么要假设特征之间相互独立呢？原因其实也很简单，因为如果特征之间不相互独立，那么每一个特征其实并不能单独作为一个独立的特征参与计算，而是要考虑到排列组合，特征A在特征B影响下是一种情况，特征A在特征C影响下是另外一种情况，特征A在特征B和特征C影响下又是一种情况······如果有5个特征，每个特征有10个特征值，那么此时可能的情况就要10的5次方种

​ 在开头的例子中我也提到，生活中很多事情无法判断一个“绝对”，但是为了能分类，我们会通过其概率值来进行判断。

​ 假设现在我们有一个待分类项XXX，这个待分类项有很多的特征α1,α2,α3,…,αn\alpha_1,\alpha_2,\alpha_3,…,\alpha_nα1​,α2​,α3​,…,αn​，且这些特征之间相互独立互不影响。我们现在还有一个类别集合CCC，集合CCC中的类别包括y1,y2,y3,…,yny_1,y_2,y_3,…,y_ny1​,y2​,y3​,…,yn​。

​ 对于每一个P(yi∣αi)P(y_i|\alpha_i)P(yi​∣αi​)，表示的意思是在特征αi\alpha_iαi​的条件下，yiy_iyi​类别的发生概率。比如前文提到的，在特征“既上早自习又上晚自习”的条件下，“能够保研”类别的发生概率。如果这个概率比较大，这个待分类项被分类到yiy_iyi​的概率也就越大。

​ 但是，由于类别有很多，只通过一个P(yi∣αi)P(y_i|\alpha_i)P(yi​∣αi​)就判断是否能分到这个类中是不合理的。我们还需要去观察观察别的类别。通过比较P(y1∣αi)P(y_1|\alpha_i)P(y1​∣αi​)、P(y2∣αi)P(y_2|\alpha_i)P(y2​∣αi​)、P(y3∣αi)P(y_3|\alpha_i)P(y3​∣αi​)、······、P(yn∣αi)P(y_n|\alpha_i)P(yn​∣αi​)的大小，我们找到最大的概率P(yk∣αi)P(y_k|\alpha_i)P(yk​∣αi​)，说明在αi\alpha_iαi​特征条件下，应该被分到yky_kyk​类。

​ 但是，由于分到哪一个类别中不能仅仅看一个特征αi\alpha_iαi​，因为是由待分类项是由多个特征构成的，当我们比较P(yi∣X)P(y_i|X)P(yi​∣X)的大小时才更加合理。这就引出了一个问题，我们可以求出P(yi∣αi)P(y_i|\alpha_i)P(yi​∣αi​)的概率，因为这是样本数据集中的概率决定的，如何求P(yi∣X)P(y_i|X)P(yi​∣X)的概率呢？

​ 这时候就要利用到我们上文所说的贝叶斯公式。根据贝叶斯公式，
P(yi∣X)=P(X∣yi)P(yi)P(X)P(y_i|X)=\frac{P(X|y_i)P(y_i)}{P(X)} P(yi​∣X)=P(X)P(X∣yi​)P(yi​)​
其中XXX是待分类项，P(X)P(X)P(X)指的是各特征出现的概率，在特征不变的情况下，可以看做常数，所以P(yi∣X)正比于P(X∣yi)P(yi)P(y_i|X)正比于P(X|y_i)P(y_i)P(yi​∣X)正比于P(X∣yi​)P(yi​)。其中，
P(X∣yi)=P(α1,α2,α3,…,αn∣yi)=P(α1∣yi)P(α2∣yi)P(α3∣yi)⋅⋅⋅P(αn∣yi)P(X|y_i)=P(\alpha_1,\alpha_2,\alpha_3,…,\alpha_n|y_i)=P(\alpha_1|y_i)P(\alpha_2|y_i)P(\alpha_3|y_i)···P(\alpha_n|y_i) P(X∣yi​)=P(α1​,α2​,α3​,…,αn​∣yi​)=P(α1​∣yi​)P(α2​∣yi​)P(α3​∣yi​)⋅⋅⋅P(αn​∣yi​)
这是由于之前的假设，各个特征之间相互独立而决定的。到这一步，我们也不难发现，其实贝叶斯公式最大的作用就是，将位于条件位置上的X转换到非条件位置上，这样就可以利用事件独立性原理进行展开。这样我们就可以求出P(X∣yi)P(yi)P(X|y_i)P(y_i)P(X∣yi​)P(yi​)。最后我们只需要比较其大小即可。

​ 所以我们可以定义朴素贝叶斯函数classify(X)classify(X)classify(X)，
classify(X)=argmaxP(yi)P(α1∣yi)P(α2∣yi)P(α3∣yi)⋅⋅⋅P(αn∣yi)classify(X)=argmaxP(y_i)P(\alpha_1|y_i)P(\alpha_2|y_i)P(\alpha_3|y_i)···P(\alpha_n|y_i) classify(X)=argmaxP(yi​)P(α1​∣yi​)P(α2​∣yi​)P(α3​∣yi​)⋅⋅⋅P(αn​∣yi​)
即
classify(X)=argmaxP(yi)∏k=1nP(αk∣yi)classify(X)=argmaxP(y_i)\prod_{k=1}^{n}{P(\alpha_k|y_i)} classify(X)=argmaxP(yi​)k=1∏n​P(αk​∣yi​)
argmax函数就是在所有的当中选取最大的。

下面我们来总结一下朴素贝叶斯算法：

• 设X{α1,α2,α3,…,αn}X\{\alpha_1,\alpha_2,\alpha_3,…,\alpha_n\}X{α1​,α2​,α3​,…,αn​}为一个待分类项，每个αi\alpha_iαi​为xxx的一个特征属性，且属性之间相互独立。设C{y1,y2,y3,…,yn}C\{y_1,y_2,y_3,…,y_n\}C{y1​,y2​,y3​,…,yn​}为一个待分类集合
• 通过公式P(yi)∏k=1nP(αk∣yi)P(y_i)\prod_{k=1}^{n}{P(\alpha_k|y_i)}P(yi​)∏k=1n​P(αk​∣yi​)计算P(y1∣X)、P(y2∣X)、⋅⋅⋅、P(yn∣X)P(y_1|X)、P(y_2|X)、···、P(y_n|X)P(y1​∣X)、P(y2​∣X)、⋅⋅⋅、P(yn​∣X)
• 求出最大的P(yk∣X)P(y_k|X)P(yk​∣X)，对应的yky_kyk​类即为待分类项XXX应该分得的类

三、极大似然估计

似然函数

似然函数和概率函数其实有很多的相似之处。个人觉得，这两者更像是一种互相弥补的关系，换一种说法就是，两者就是将自变量和因变量进行了交换。

我们知道条件概率：P(x∣θ)P(x|θ)P(x∣θ)，其中θ\thetaθ是作为条件，而xxx是作为事件发生的结果。比如现在有一枚均匀的硬币，我们将其投掷三次，有两次正面向上。那么xxx就是两次正面向上的结果，而θ\thetaθ就是一块硬币正面向上的概率，我们可以记作pHp_HpH​。我们可以将P(x∣θ:pH)P(x|θ:p_H)P(x∣θ:pH​)理解成在一块硬币正面向上为pHp_HpH​的条件下，投掷三次硬币两次正面向上的概率。这种情况下，我们已知θ\thetaθ，要求xxx。这是我们最常见的概率的含义。那么有没有一种情况就是，我们已知xxx，但是不知道pHp_HpH​，换句话来说，我们现在通过一些试验，能够知道投掷三次两次正面向上的概率为0.75（不是大量试验，比如做了四次试验三次是这个结果），但是由于这块硬币不是绝对均匀的（事实上真实的硬币也是如此），所以我们不知道pHp_HpH​是多少。但是我们可以根据概率的性质计算出表达式：
P(x∣pH)=C31×pH2×(1−pH)P(x|p_H)=C_3^1×p_H^2×(1-p_H) P(x∣pH​)=C31​×pH2​×(1−pH​)
当pH=0.5p_H=0.5pH​=0.5时，结果是0.375；当pH=0.6p_H=0.6pH​=0.6时，结果是0.432。由于我们实际做实验得到的结果是0.75，而0.432与这个结果更为接近，我们可以认为正面向上的概率为0.6的时候更加接近实际的正确值。而我们求出的这个概率值就是似然概率，上面求出的表达式就是似然函数。

总结：

条件概率P(x∣θ)P(x|θ)P(x∣θ)的输入有两个：x表示某一个具体的数据；θ表示模型的参数。

• 如果θ是已知确定的，x是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点x，其出现概率是多少。

• 如果x是已知确定的，θ是变量，这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数，出现x这个样本点的概率是多少。

为了方便区分，我们重新给似然概率一个符号：
L(θ∣x)=P(x∣θ)L(\theta|x)=P(x|\theta) L(θ∣x)=P(x∣θ)
前者是似然概率，后者就是普通的概率。

详细文章参考维基百科：https://zh.m.wikipedia.org/zhhans/%E4%BC%BC%E7%84%B6%E5%87%BD%E6%95%B0

最大似然估计

​ 前文我们介绍了似然函数，而最大似然估计的思想就是，对似然函数求最大值，求出最大值对应的θ\thetaθ就是导致事件xxx发生的最有可能的θ\thetaθ值。

后验概率最大化

​ 有了似然函数和最大似然估计的铺垫，我们就可以重新回到贝叶斯公式。

上文我们已知：
L(θ∣x)=P(x∣θ)L(\theta|x)=P(x|\theta) L(θ∣x)=P(x∣θ)
​ 其中θ\thetaθ是模型参数，相当于前文的类别集合CCC；xxx是样本点，相当于待分类项XXX，所以类似的我们也可以得到下面这个式子：
L(yi∣X)=P(X∣yi)L(y_i|X)=P(X|y_i) L(yi​∣X)=P(X∣yi​)

​

四、贝叶斯估计

平滑处理：
使用朴素贝叶斯算法的时候，有可能数据集样本库中某个特征下的样本为0，那么由于连乘，整个P(yi∣X)P(y_i|X)P(yi​∣X)都是0，这是不合理的。因为我们不能因为一个事件没有被观察到就确认该事件发生概率为0。所以我们要进行拉普拉斯平滑处理，以避免这种现象对整个样本造成影响。

拉普拉斯平滑处理：
P(xi∣y)=Nyi+αNy+nαP(x_i|y)=\frac{N_{yi}+\alpha}{N_y+n\alpha} P(xi​∣y)=Ny​+nαNyi​+α​
其中，NyiN_{yi}Nyi​表示类y所有样本中特征为αi\alpha_iαi​的样本的数量，NyN_yNy​表示所有类y中样本的数量，α\alphaα是平滑值，α∈[0,1]\alpha∈[0,1]α∈[0,1]。nnn表示特征总数。

使用拉普拉斯平滑处理的算法称为贝叶斯估计。