文章目录

• 前言
• 一、实现
• • 1.1 核心步骤和复杂度
  • 1.2 伪码和java示例
  • 1.3 动图示例
• 二、应用
• • 2.1 寻找最短路径
  • 2.2 拓扑排序
  • 2.3 最小生成树
• 三、LeetCode 实战
• • 3.1二叉树的层序遍历
  • 3.2 找树左下角的值
  • 3.3单词接龙
• 参考

前言

广度优先搜索（Breadth First Search，简称 BFS），是一种遍历图存储结构的一种算法，它既适用于无向图，也适用于有向图。

BFS 算法的基本思想是从一个起始顶点开始，依次访问其相邻的未被访问过的顶点，并将它们加入到一个队列中，然后从队列中取出一个顶点作为新的起始顶点，重复上述过程，直到队列为空或者找到目标顶点为止。

BFS 算法的特点是：

• 从一个顶点开始，按层次访问其相邻的顶点，然后再访问下一层的顶点，直到遍历完所有的顶点。
• 使用队列来存储待访问的顶点，保证先进先出的顺序。
• 能够找到最短路径，适用于寻路等问题。

bfs算法的优点是：

• 始终可以保证找到问题的解，如果有多个解，可以找到最优解。
• 运行速度快，不需要回溯操作。

BFS 算法的缺点是：

• 需要存储每一层的顶点，占用空间大，可能会超出内存限制。
• 对于深度较大的图，可能会花费很长的时间。

BFS 算法有很多应用场景，例如：

• 寻找最短路径，如迷宫寻路、地图导航等。
• 判断两个顶点之间是否连通或者属于同一个连通分量。
• 发现图中的环或者判断图是否为二分图。
• 人工智能中的搜索策略，如广度优先爬虫、机器人探索等。
• 最小生成树。
• 垃圾回收。
• 网络流。

一、实现

1.1 核心步骤和复杂度

BFS 算法的核心步骤如下：

• 从一个起始节点开始，将其加入一个队列（queue）中。
• 重复以下操作，直到队列为空或找到目标节点：
  • 弹出队列的第一个节点，访问它，并将其标记为已访问。
  • 将该节点的所有未访问的邻居节点加入队列的末尾。
• 返回访问过的节点或找到的目标节点。

BFS 的时间复杂度为O(V+E)，其中V是顶点数，E是边数。每个顶点最多被访问一次，每条边也最多被访问一次，因此总的时间复杂度为O(V+E)。

空间复杂度取决于存储访问状态和待访问顶点的数据结构。对于邻接表表示图，空间复杂度为O(V+E)，其中V是顶点数，E是边数。需要使用一个集合记录已经访问过的顶点，一个队列存储待访问的顶点。在最坏情况下，所有顶点都会被访问到，所有顶点都会被加入队列，因此空间复杂度为O(V+E)。

1.2 伪码和java示例

伪码如下：

# 伪码
BFS(start, target):# 创建一个队列queue = new Queue()# 创建一个集合，用于记录已访问的顶点visited = new Set()# 将起始顶点加入队列和集合queue.enqueue(start)visited.add(start)# 循环直到队列为空或找到目标顶点while queue is not empty:# 弹出队列的第一个顶点node = queue.dequeue()# 访问该顶点visit(node)# 如果该顶点是目标顶点，返回if node == target:return node# 遍历该顶点的所有未访问的邻居顶点for neighbor in node.neighbors:# 如果邻居顶点没有被访问过，将其加入队列和集合if neighbor not in visited:queue.enqueue(neighbor)visited.add(neighbor)# 如果没有找到目标顶点，返回空return null

java示例代码如下：

// Java
import java.util.*;public class BFS {// 定义图的顶点类static class Node {int val; // 顶点的值List neighbors; // 顶点的邻居列表public Node(int val) {this.val = val;this.neighbors = new ArrayList<>();}}// BFS 算法public static Node bfs(Node start, Node target) {// 创建一个队列Queue queue = new LinkedList<>();// 创建一个集合，用于记录已访问的顶点Set visited = new HashSet<>();// 将起始顶点加入队列和集合queue.offer(start);visited.add(start);// 循环直到队列为空或找到目标顶点while (!queue.isEmpty()) {// 弹出队列的第一个顶点Node node = queue.poll();// 访问该顶点visit(node);// 如果该顶点是目标顶点，返回if (node == target) {return node;}// 遍历该顶点的所有未访问的邻居顶点for (Node neighbor : node.neighbors) {// 如果邻居顶点没有被访问过，将其加入队列和集合if (!visited.contains(neighbor)) {queue.offer(neighbor);visited.add(neighbor);}}}// 如果没有找到目标顶点，返回空return null;}// 访问顶点的方法，打印顶点的值public static void visit(Node node) {System.out.println(node.val);}// 测试方法public static void main(String[] args) {// 创建一个图Node n1 = new Node(1);Node n2 = new Node(2);Node n3 = new Node(3);Node n4 = new Node(4);Node n5 = new Node(5);Node n6 = new Node(6);n1.neighbors.add(n2);n1.neighbors.add(n3);n2.neighbors.add(n4);n3.neighbors.add(n4);n3.neighbors.add(n5);n4.neighbors.add(n6);n5.neighbors.add(n6);// 调用 BFS 算法，从顶点 1 开始，寻找顶点 6Node result = bfs(n1, n6);// 打印结果if (result != null) {System.out.println("找到了目标顶点：" + result.val);} else {System.out.println("没有找到目标顶点");}}
}

1.3 动图示例

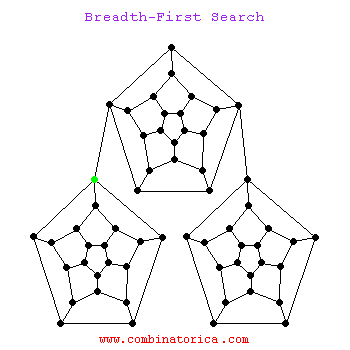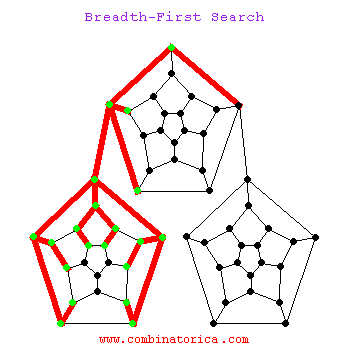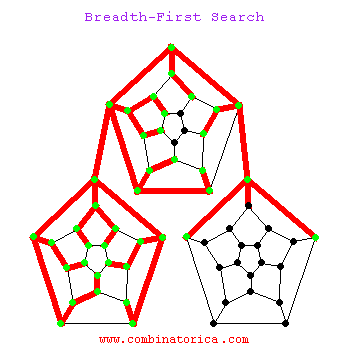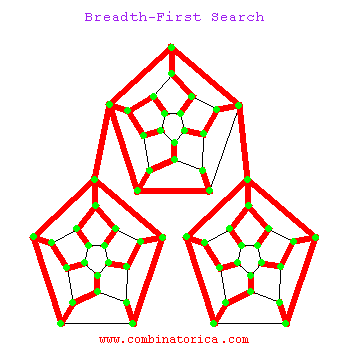
二、应用

2.1 寻找最短路径

BFS 算法可以用于寻找图中两个顶点之间的最短路径，即经过最少的边数的路径。这是因为 BFS 算法是按照层次遍历图的，每一层的顶点都与起始顶点的距离相同，因此当找到目标顶点时，就是最短路径。

为了寻找最短路径，我们需要在 BFS 算法的基础上做一些修改：

• 除了记录已访问的顶点，我们还需要记录每个顶点的前驱顶点，即从哪个顶点到达该顶点的。
• 当找到目标顶点时，我们需要从目标顶点开始，沿着前驱顶点的链表，逆序输出最短路径。

伪码如下：

# 伪码
BFS(start, target):# 创建一个队列queue = new Queue()# 创建一个集合，用于记录已访问的顶点visited = new Set()# 创建一个字典，用于记录每个顶点的前驱顶点prev = new Map()# 将起始顶点加入队列和集合queue.enqueue(start)visited.add(start)# 循环直到队列为空或找到目标顶点while queue is not empty:# 弹出队列的第一个顶点node = queue.dequeue()# 访问该顶点visit(node)# 如果该顶点是目标顶点，返回if node == target:# 创建一个列表，用于存储最短路径path = new List()# 从目标顶点开始，沿着前驱顶点的链表，逆序输出最短路径while node != null:# 将当前顶点加入路径的开头path.insert(0, node)# 更新当前顶点为其前驱顶点node = prev[node]# 返回最短路径return path# 遍历该顶点的所有未访问的邻居顶点for neighbor in node.neighbors:# 如果邻居顶点没有被访问过，将其加入队列和集合，并记录其前驱顶点if neighbor not in visited:queue.enqueue(neighbor)visited.add(neighbor)prev[neighbor] = node# 如果没有找到目标顶点，返回空return null

2.2 拓扑排序

BFS 算法还可以用于对有向无环图（DAG）进行拓扑排序，即按照顶点的依赖关系，将顶点排列成一个线性序列，使得对于任意一条有向边 (u, v)，u 都在 v 的前面。

为了进行拓扑排序，我们需要在 BFS 算法的基础上做一些修改：

• 我们需要记录每个顶点的入度，即有多少条边指向该顶点。
• 我们需要从入度为 0 的顶点开始，将其加入队列，然后依次弹出队列中的顶点，将其加入拓扑序列，并将其所有邻居顶点的入度减一，如果邻居顶点的入度变为 0，也将其加入队列。
• 如果最后拓扑序列中的顶点数等于图中的顶点数，说明拓扑排序成功，否则说明图中存在环，无法进行拓扑排序。

伪码如下：

# 伪码
BFS(graph):# 创建一个队列queue = new Queue()# 创建一个列表，用于存储拓扑序列topo = new List()# 创建一个字典，用于记录每个顶点的入度indegree = new Map()# 遍历图中的每个顶点，初始化其入度for node in graph.nodes:indegree[node] = 0# 遍历图中的每条边，更新每个顶点的入度for edge in graph.edges:indegree[edge.to] += 1# 遍历图中的每个顶点，将入度为 0 的顶点加入队列for node in graph.nodes:if indegree[node] == 0:queue.enqueue(node)# 循环直到队列为空while queue is not empty:# 弹出队列的第一个顶点node = queue.dequeue()# 将该顶点加入拓扑序列topo.append(node)# 遍历该顶点的所有邻居顶点，将其入度减一，如果入度为 0，将其加入队列for neighbor in node.neighbors:indegree[neighbor] -= 1if indegree[neighbor] == 0:queue.enqueue(neighbor)# 如果拓扑序列中的顶点数等于图中的顶点数，返回拓扑序列，否则返回空if len(topo) == len(graph.nodes):return topoelse:return null

2.3 最小生成树

BFS 算法还可以用于求解无向连通图的最小生成树（MST），即一个包含图中所有顶点的无环子图，使得其边的权值之和最小。

为了求解最小生成树，我们需要在 BFS 算法的基础上做一些修改：

• 我们需要给每条边赋予一个权值，表示该边的长度或者代价。
• 我们需要从任意一个顶点开始，将其加入队列，然后依次弹出队列中的顶点，将其加入最小生成树的顶点集合，并将其所有邻居顶点的边加入一个优先队列，按照边的权值从小到大排序。
• 我们需要循环直到优先队列为空或者最小生成树的顶点集合等于图中的顶点集合，每次从优先队列中取出最小的边，如果该边的两个顶点都已经在最小生成树的顶点集合中，说明该边会形成环，跳过该边，否则将该边加入最小生成树的边集合，并将该边的另一个顶点加入队列。
• 如果最后最小生成树的顶点集合等于图中的顶点集合，说明最小生成树构造成功，否则说明图不连通，无法构造最小生成树。

伪码如下：

# 伪码
BFS(graph):# 创建一个队列queue = new Queue()# 创建一个优先队列，用于存储边，按照权值从小到大排序pq = new PriorityQueue()# 创建一个集合，用于存储最小生成树的顶点mst_nodes = new Set()# 创建一个列表，用于存储最小生成树的边mst_edges = new List()# 从图中的任意一个顶点开始，将其加入队列和最小生成树的顶点集合start = graph.nodes[0]queue.enqueue(start)mst_nodes.add(start)# 循环直到队列为空或者最小生成树的顶点集合等于图中的顶点集合while queue is not empty and len(mst_nodes) < len(graph.nodes):# 弹出队列的第一个顶点node = queue.dequeue()# 遍历该顶点的所有邻居顶点，将其边加入优先队列for neighbor in node.neighbors:edge = get_edge(node, neighbor) # 获取两个顶点之间的边pq.enqueue(edge)# 循环直到优先队列为空或者找到一条合适的边while pq is not empty:# 从优先队列中取出最小的边edge = pq.dequeue()# 如果该边的两个顶点都已经在最小生成树的顶点集合中，跳过该边if edge.from in mst_nodes and edge.to in mst_nodes:continue# 否则将该边加入最小生成树的边集合mst_edges.append(edge)# 并将该边的另一个顶点加入队列和最小生成树的顶点集合if edge.from in mst_nodes:queue.enqueue(edge.to)mst_nodes.add(edge.to)else:queue.enqueue(edge.from)mst_nodes.add(edge.from)# 跳出循环break# 如果最后最小生成树的顶点集合等于图中的顶点集合，返回最小生成树的边集合，否则返回空if len(mst_nodes) == len(graph.nodes): return mst_edges else: return null

三、LeetCode 实战

3.1二叉树的层序遍历

102. 二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

public List> levelOrder(TreeNode root) {List> ans = new ArrayList<>();if (root == null) return ans;Queue queue = new LinkedList<>();queue.offer(root); // 将根节点入队queue.offer(null); // 将空元素入队作为分隔符List tmp = new ArrayList<>(); // 存储每一层的节点值while (!queue.isEmpty()) {TreeNode node = queue.poll(); // 出队一个节点if (node == null) { // 如果节点是空元素，说明一层结束了ans.add(tmp); // 将当前层的列表添加到结果中tmp = new ArrayList<>(); // 重置当前层的列表if (!queue.isEmpty()) queue.offer(null); // 如果队列不为空，再次添加一个空元素作为分隔符} else { // 如果节点不是空元素，说明还在当前层tmp.add(node.val); // 将节点值添加到当前层的列表中if (node.left != null) queue.offer(node.left); // 将左子节点入队if (node.right != null) queue.offer(node.right); // 将右子节点入队}}return ans;
}

3.2 找树左下角的值

513. 找树左下角的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

public int findBottomLeftValue(TreeNode root) {int leftmost = root.val; // 初始化最左边的节点值为根节点值Queue queue = new LinkedList<>();queue.offer(root); // 将根节点入队while (!queue.isEmpty()) {int size = queue.size(); // 记录当前层的节点个数for (int i = 0; i < size; i++) {TreeNode node = queue.poll(); // 出队一个节点if (i == 0) leftmost = node.val; // 如果是当前层的第一个节点，更新最左边的节点值if (node.left != null) queue.offer(node.left); // 将左子节点入队if (node.right != null) queue.offer(node.right); // 将右子节点入队}}return leftmost; // 返回最左边的节点值
}

3.3单词接龙

127. 单词接龙

字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk：

• 每一对相邻的单词只差一个字母。
• 对于 1 <= i <= k 时，每个 si 都在 wordList 中。注意， beginWord 不需要在 wordList 中。
• sk == endWord

给你两个单词 beginWord 和 endWord 和一个字典 wordList ，返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列，返回 0 。

单词集合中的每个单词是节点，只有一个位置字母不同的单词可以相连，求起点和终点的最短路径长度，可以等价于无向图求最短路，广搜最为合适，广搜只要搜到了终点，那么一定是最短的路径。因为广搜就是以起点中心向四周扩散的搜索。还有两个注意点：

1. 无向图，需要用标记位，标记着节点是否走过，否则就会死循环。
2. 集合是数组型的，可以转成 Set 结构，查找更快一些。

public int ladderLength(String beginWord, String endWord, List wordList) {int ans = 0;Set words = new HashSet<>(wordList); // 单词列表转为Setif (!words.contains(endWord)) {return 0; // 如果目标单词不在单词集合中，直接返回0}Set nextLevel = new HashSet<>();nextLevel.add(beginWord); // 将起始单词加入到第一个队列中ans++; // 初始化路径长度为1while (!nextLevel.isEmpty()) { // 使用一个循环，直到队列为空ans++; // 路径长度加一Set tmpSet = new HashSet<>(); // 创建一个临时队列，用于存储下一层的搜索路径for (String s: nextLevel) { // 遍历第一个队列中的每个单词char [] chs = s.toCharArray(); // 将单词转换为字符数组for (int i = 0; i < chs.length; i++) { // 遍历每个字符的位置char old = chs[i]; // 保存原来的字符，避免重复创建字符数组for (char ch = 'a'; ch <= 'z'; ch++) { // 遍历每个可能的字符chs[i] = ch; // 直接修改字符数组，避免创建新的字符串String tmp = new String(chs); // 将字符数组转换为新的单词if (nextLevel.contains(tmp)) {continue; // 如果第一个队列中包含了新的单词，跳过}if (words.contains(tmp)) { // 如果单词集合中包含了新的单词tmpSet.add(tmp); // 将它加入到临时队列中words.remove(tmp); // 从单词集合中移除已经访问过的单词，避免重复访问}if (tmp.equals(endWord)) { // 如果新的单词等于目标单词，说明找到了一个最短路径，返回路径长度return ans;}}chs[i] = old; // 恢复原来的字符}}nextLevel = tmpSet; // 将临时队列赋值给第一个队列，作为下一层的搜索路径}return 0; // 如果循环结束，说明没有找到路径，返回0
}

参考

1. https://leetcode.cn/tag/breadth-first-search/problemset/