机器学习笔记之集成学习——Bagging

• 引言
• • 回顾：偏差、方差、噪声
  • 自助采样法(Bootstrapping Sampling\text{Bootstrapping Sampling}Bootstrapping Sampling)
  • Bagging\text{Bagging}Bagging过程介绍
  • 随机森林
  • 什么情况下使用Bagging\text{Bagging}Bagging
  • • 什么学习器是不稳定学习器

引言

上一节介绍了模型泛化误差的组成——偏差、方差、噪声。本节将介绍降低方差的集成学习方法——Bagging\text{Bagging}Bagging。

回顾：偏差、方差、噪声

学习模型的泛化误差由三部分组成：偏差、方差、噪声。其中噪声是数据集合自身属性，其噪声是客观存在的。因而，我们关注的目标更多在于偏差、方差的降低过程。

其中，偏差较高的核心原因在于：

• 训练过程过短导致的欠拟合(Underfitting\text{Underfitting}Underfitting)现象：这种情况我们需要延长训练过程的执行时间；
• 模型的复杂度不够：即便训练过程执行了足够长的时间，但模型的拟合能力依然较差。此时需要提升模型的复杂程度；或者使用Boosting,Stacking\text{Boosting,Stacking}Boosting,Stacking等集成学习方法。

相反，关于方差较高的核心原因在于：

• 即便是样本特征的简单扰动，也能够使学习模型产生复杂变化。也就是说，学习模型的复杂程度已经远超样本特征的复杂程度。针对该情况，可以尝试简化模型的复杂度。
• 针对学习模型的过拟合(Overfitting\text{Overfitting}Overfitting)现象，可以使用各种预防过拟合的方式。其中集成学习方法中包含Bagging,Stacking\text{Bagging,Stacking}Bagging,Stacking。

自助采样法(Bootstrapping Sampling\text{Bootstrapping Sampling}Bootstrapping Sampling)

自助采样法主要针对模型训练过程中，关于数据集合D\mathcal DD的使用使用不够完整导致的估计偏差。自助采样法的采样过程表示如下：
机器学习(周志华著)P27.

• 已知一个包含NNN个样本的数据集合D\mathcal DD，我们需要通过采样得到相应的数据集合D′\mathcal D'D′；
• 随机从数据集合D\mathcal DD中采出一个样本xxx；
• 将xxx复制，并将复制结果放入数据集合D′\mathcal D'D′中；
• 将样本xxx放回数据集合D\mathcal DD中；
• 重复执行步骤2−42-42−4共NNN次，最终得到一个包含NNN个样本的数据集合D′\mathcal D'D′。

我们可以发现，这种自助采样方式存在：某些样本可能会在D′\mathcal D'D′中出现若干次，而某些样本可能不会出现。那么样本在NNN次采样中总是无法被采样的概率是：(1−1N)N(1 - \frac{1}{N})^N(1−N1​)N，也就是说，如果原始集合D\mathcal DD的样本数量趋近于无穷大，那么D′\mathcal D'D′中始终不会从D\mathcal DD采样的概率是：
limN→∞(1−1N)N=1e≈0.368\mathop{\text{lim}}\limits_{N \to \infty} \left(1 - \frac{1}{N}\right)^N = \frac{1}{e} \approx 0.368N→∞lim​(1−N1​)N=e1​≈0.368

我们可以尝试从代码的角度观察一下这个结果：

def BootstrapingSampling(SampleNum):def GetGenerateRatio(D):idx = np.random.randint(0, len(D), size=SampleNum)D_ = [D[i] for i in idx]return 1 - (len(set(D_)) / len(D))D = [i for i in range(SampleNum)]return GetGenerateRatio(D)def DrawPicture():GenerateRatioList = list()for SampleNum in range(10,100000,100):Ratio = BootstrapingSampling(SampleNum)GenerateRatioList.append(Ratio)x = [i for i in range(len(GenerateRatioList))]plt.scatter(x,GenerateRatioList,s=4,c="tab:blue")plt.plot(x,[0.368 for _ in x],c="tab:orange")plt.show()if __name__ == '__main__':DrawPicture()

返回图像结果如下：

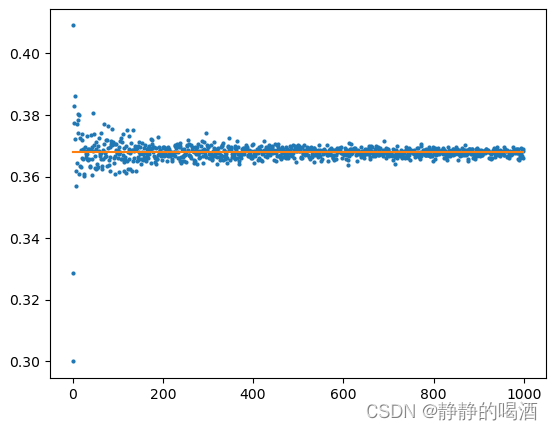
可以看出，仅在样本量极少的情况下(仅包含几百个样本左右的数据集)，这个比值会有较大的波动。否则，总是会有数据总量约13\frac{1}{3}31​的样本用于测试。这样的测试结果也被称作包外估计(Out-of-bag Estimate\text{Out-of-bag Estimate}Out-of-bag Estimate)

因此，自助采样法它的适用范围：

• 数据集数量较小；
• 无法有效的划分训练/测试集；
  我们更希望训练集和测试集之间符合相同的分布。但是如果数据特征过于复杂，无法通过人工的方式划分出一套优秀的训练/测试集，可以尝试使用该方法。

但是与之相对的，自助采样法产生的数据集相比真实数据集消掉了约36.836.836.8%的数据信息，这改变了初始数据集的分布，从而引入了估计偏差。因而在样本足够充足的条件下，不适宜使用自助采样法。

Bagging\text{Bagging}Bagging过程介绍

Bagging\text{Bagging}Bagging是Bootstrap Aggrgrating\text{Bootstrap Aggrgrating}Bootstrap Aggrgrating的缩写，这个过程可表示为：

• 在Bagging\text{Bagging}Bagging过程中，每次训练NNN个模型，每个模型被称作基学习器(Base Learner\text{Base Learner}Base Learner)，并且每一个基学习器均是独立训练。也就是说，各学习器之间的训练过程是并行的；
• 采用自助采样法生成若干个数据集分别对每个基学习器进行训练；
• 在得到训练好的NNN个模型之后，关于最终的输出结果，根据它的任务类型对输出结果进行描述：
  • 如果是回归(Regression\text{Regression}Regression)任务，将每个模型的输出结果做均值操作；
  • 如果是分类(Classification\text{Classification}Classification)任务，那么最终分类结果通过多数表决(Majority voting\text{Majority voting}Majority voting)的方式决定——每一个模型输出一个类别，对这些类别投票，选做多的结果作为最终类别。

随机森林

随机森林(Random Forest,RF\text{Random Forest,RF}Random Forest,RF)是Bagging\text{Bagging}Bagging的一个扩展变体。

• Bagging\text{Bagging}Bagging过程中以决策树(Decision Tree\text{Decision Tree}Decision Tree)作为基学习器；
• 通常为每一个基学习器随机选择特征子集;
  • 对于传统决策树在划分属性时，对于每一个结点，划分属性时选择当前结点所有属性集合(假设集合中包含ddd个属性)中的最优属性；
  • 对于随机森林的属性划分，对于随机森林中的每一个基决策树，基决策树中的每个结点，从该结点对应的属性集合中随机选择一个‘包含kkk个属性的子集’，并从该子集中选择一个最优属性用于划分。
  • 每个基决策树中的每个结点均执行上述操作。而子集中包含的属性数量kkk则是描述‘随机性的引入程度’。
  • 当k=1k=1k=1时，每一个属性自成一个子集，即随机选择一个属性进行划分;
  • 当k=dk=dk=d时，此时仅包含一个集合，此时和传统决策树的划分方式相同。

整理：从整个随机森林的角度出发，它的特点有两个部分：

• 对于各训练模型的数据集：每个训练模型用到的数据集使用Bagging\text{Bagging}Bagging方式进行获取；

• 对于各训练模型(决策树)，在每棵树划分结点的过程中，每一次划分结点并非从当前属性中选择最优属性，而是先划分一个属性子集，再从属性子集中选择最优属性。

  这种处理方式的优势可以使模型中的各决策树之间存在差异性。而最终集成结果的泛化性能随着这种差异性而进一步提升。
  这里的泛化性能是指‘针对不同的任务类型(分类、回归)’产生的集成后结果的性能。

从随机森林的角度观察Bagging\text{Bagging}Bagging集成方法的优势：我们可以有效地降低方差的同时，不会增加整体的泛化误差；这意味着偏差并没有产生影响。也就是说，Bagging\text{Bagging}Bagging仅仅改善了方差，并且没有使偏差增大。

随着随机森林中基学习器数量的增加，关于回归任务的泛化误差结果表示如下：

import matplotlib.pyplot as plt
from tqdm import trange
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_bostonboston = load_boston()
XTrain,XTest,YTrain,YTest = train_test_split(boston.data,boston.target)MSEListTrain = list()
MSEListTest = list()
for EstimatorNum in trange(1,150,1):Estimator = RandomForestRegressor(n_estimators=EstimatorNum)Estimator.fit(XTrain,YTrain)ScoresTrain = cross_val_score(Estimator,XTrain,YTrain,scoring = "neg_mean_squared_error",cv=5).mean()ScoresTest = cross_val_score(Estimator,XTest,YTest,scoring = "neg_mean_squared_error",cv=5).mean()MSEListTrain.append(ScoresTrain * -1)MSEListTest.append(ScoresTest * -1)x = [i for i in range(len(MSEListTrain))]
plt.plot(x,MSEListTrain,c="tab:blue",label="train")
plt.plot(x,MSEListTest,c="tab:orange",label="test")
plt.legend()
plt.show()

对应结果表示如下：

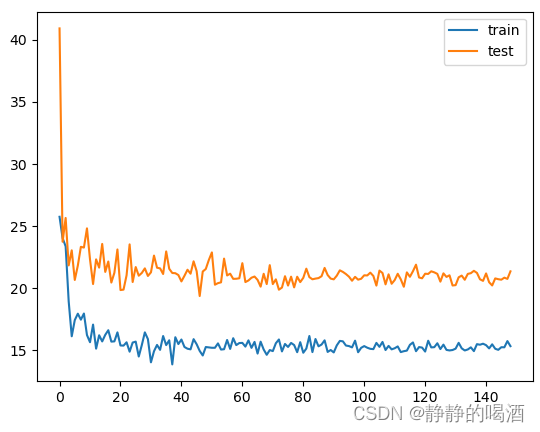
其中，横坐标表示基学习器的数量；纵坐标表示泛化误差结果。可以通过观察得到，随着基学习器数量的增加，泛化误差并没有产生过拟合的现象。这说明Bagging\text{Bagging}Bagging集成思想可以有效地抑制方差，即便是基学习器数量很多，通常不会使误差结果变差。

什么情况下使用Bagging\text{Bagging}Bagging

Bagging\text{Bagging}Bagging主要减小泛化误差中的方差。具体做法是通过训练若干个学习器，如果关于回归任务，将各学习器的预测结果取均值。

虽然是通过取均值来得到最终结果，但这种结果并不会影响均值本身，也就是偏差；反而如果获取越多的预测结果取均值，方差会越来越小。

关于什么情况下使用Bagging\text{Bagging}Bagging，那自然是在模型训练过程中，方差不可避免地增大时，使用Bagging\text{Bagging}Bagging是不错的选择。也就是说，方差的大小与训练模型自身性质相关。

通常称方差较大的模型为不稳定学习器(Unstable Learner\text{Unstable Learner}Unstable Learner)，依然以回归任务为例，这里假设真实模型为f(X)f(\mathcal X)f(X)，基学习器为h(i)(X)(i=1,2,⋯,m)h^{(i)}(\mathcal X)(i=1,2,\cdots,m)h(i)(X)(i=1,2,⋯,m)；其中iii表示基学习器的编号。至此，通过Bagging\text{Bagging}Bagging集成思想得到的近似模型f^(X)\hat f(\mathcal X)f^​(X)表示如下：
f^(X)=1m∑i=1mh(i)(X)=E[h(X)]\hat f(\mathcal X) = \frac{1}{m}\sum_{i=1}^m h^{(i)}(\mathcal X) = \mathbb E[h(\mathcal X)]f^​(X)=m1​i=1∑m​h(i)(X)=E[h(X)]

从方差的数学性质角度观察，它必然是一个非负结果。因而有：
Var(x)≥0⇔E(x2)−[E(x)]2≥0⇔[E(x)]2≤E(x2)\text{Var}(x) \geq 0 \Leftrightarrow \mathbb E(x^2) - [\mathbb E(x)]^2 \geq 0 \Leftrightarrow [\mathbb E(x)]^2 \leq \mathbb E(x^2) Var(x)≥0⇔E(x2)−[E(x)]2≥0⇔[E(x)]2≤E(x2)
因而有：
其中f(X)f(\mathcal X)f(X)是真实模型，它不是随机变量，因而E[f(X)]=f(X)\mathbb E[f(\mathcal X)] = f(\mathcal X)E[f(X)]=f(X).
{f(X)−f^(X)}2={E[f(X)]−E[h(X)]}2≤E[(f(x)−h(x))2]⇔{E[h(X)]}2≤E[h(X)2]\{f(\mathcal X) - \hat f(\mathcal X)\}^2 = \{\mathbb E[f(\mathcal X)] - \mathbb E[h(\mathcal X)]\}^2 \leq \mathbb E\left[(f(x) - h(x))^2\right] \Leftrightarrow \{\mathbb E[h(\mathcal X)]\}^2 \leq \mathbb E\left[h(\mathcal X)^2\right]{f(X)−f^​(X)}2={E[f(X)]−E[h(X)]}2≤E[(f(x)−h(x))2]⇔{E[h(X)]}2≤E[h(X)2]

那什么时候方差结果取等？意味着mmm个基学习器h(i)(X)(i=1,2,⋯,m)h^{(i)}(\mathcal X)(i=1,2,\cdots,m)h(i)(X)(i=1,2,⋯,m)均相等的时候方差取等。取等意味着使用基学习器h(X)h(\mathcal X)h(X)近似f(X)f(\mathcal X)f(X)不会得到优化，因为所有基学习器均相同有什么好优化的~

相反，如果各基学习器之间存在差异，使用基学习器这种方式降低方差是有效果的。

整理：不稳定学习器，基于它的各基学习器之间在训练过程中存在差异，这种差异在使用Bagging\text{Bagging}Bagging处理时，得到的结果能够有效降低方差。

什么学习器是不稳定学习器

例如决策树，它并不是一个稳定的学习器。当数据集合发生变化时，它不仅影响的是样本数量的变化，并且还影响各属性比例的变化。可能存在数据集合发生变化后，决策树选择属性的顺序发生变化；

相反，如线性回归(Linear Regression\text{Linear Regression}Linear Regression)，它就是一个稳定的学习器。在样本趋势被描述完成后，即便存在少量样本由于高噪声原因，与样本趋势不相似，但几乎不影响模型的趋势。

相关参考：
5.2 Bagging【斯坦福21秋季：实用机器学习中文版】