目录

• 0.参考链接
• 1.李群
• • 1.0 李群从何而来
  • 1.1 群的定义
  • 1.2李群的定义
• 2.李代数
• • 2.0李代数空间
  • 2.1李代数定义

0.参考链接

   ①视觉SLAM基础——李群和李代数
   ②如何通俗地解释李群和李代数的关系？
   ③李群与李代数+补充理解
   ④离散复习笔记——代数结构——幺元、零元、逆元——三个元

1.李群

1.0 李群从何而来

   通常其运动变化我们可以使用旋转加平移进行表示,即P′=RP+tP'=RP+tP′=RP+t。但是在实际中，我们时常想要知道这一微小的变化量，不能一直将每一次变化都记录下来，这时候就联想到了导数，表示的正是在某一点的一个变化率。可是对于平移ttt来说，其是具有加法运算的，但是对于RRR来说，两个旋转矩阵相加，是没有意义的，而且相加之后是破坏了旋转矩阵RRT=ERR^T=ERRT=E的性质的。
   矩阵对于乘法是封闭的，即假设相机进行了两次连续的旋转，旋转矩阵分别为R1R_{1}R1​和R2R_{2}R2​, 这两个矩阵相乘后得到的也是个旋转矩阵，表示了总的旋转。平移矩阵ttt和旋转矩阵RRR都是李群的一种，虽然其不具有加法运算，但是当把其映射到李代数空间上时，就具有了加法的性质，在李代数上进行加法计算后，或者说是导数运算后，再将其映射到对应的李群即可。

1.1 群的定义

   群（group）是一种集合加上一种运算的代数结构。把集合记为AAA，运算记为⋅\cdot⋅,群就可以记为G=(A,⋅)G=(A,\cdot)G=(A,⋅)。群结构保证了在群上的运算具有良好的性质。
  ​ 三维旋转矩阵构成了特殊正交群：
SO(3)={R∈R3×3∣RRT=E,det(R)=1}SO(3)=\left\{ R \in \mathbb R^{3 \times 3} |RR^T=E,det(R)=1 \right\}SO(3)={R∈R3×3∣RRT=E,det(R)=1}
  ​ 三维变换矩阵构成了特殊欧氏群:
SE(3)={T=[Rt0T1]∈R4×4∣R∈SO(3),t∈R3}SE(3)=\left\{ T=\begin{bmatrix} R& t \\ 0^T & 1\end{bmatrix} \in \mathbb R^{4 \times 4} | R \in SO(3),t \in \mathbb R^3\right\}SE(3)={T=[R0T​t1​]∈R4×4∣R∈SO(3),t∈R3}
  也就是说，群的本质是对矩阵的性质描述！群是相同性质矩阵集合！
  因此，群应该满足封闭性、结合性、幺元、逆元四种特性,以特殊正交群为例，则对应：
  封闭性：AB∈SO(3)AB \in SO(3)AB∈SO(3)
  结合性：(AB)C=A(BC)(AB)C=A(BC)(AB)C=A(BC)
  幺元：∃I∈,使得AI=IA=A{\exists} I \in,使得AI=IA=A∃I∈,使得AI=IA=A
  逆元：AB∈SO(3)AB \in SO(3)AB∈SO(3)使得AA−1=A−1A=IAA^{-1}=A^{-1}A=IAA−1=A−1A=I

1.2李群的定义

   李群就是具有连续（光滑）性质的群。即具有群结构的光滑微分流形，其群作用与微分结构相容。
  想象你拿个杯子就可以在空间中以某个支点连续的旋转它，所以SO(3)它就是李群。如果你一般旋转一边移动它，也是连续的或者说光滑的运动，所以变换矩阵群SE(3)也是李群。
   回顾导数的定义，显然计算导数和进行更新时都要用到加法。但SO(3) 和SE(3) 上对矩阵加法的运算并不封闭。如果要继续采取这个迭代更新的策略势必要再想想办法，使得导数“可行”。而这就可以通过李群及其对应的李代数来实现。

2.李代数

2.0李代数空间

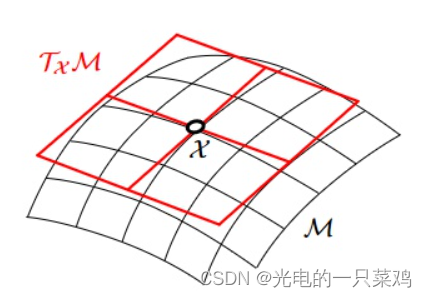
  凡是弯曲的我们都要将其线性化，也就是线性逼近，而等距同构的线性逼近就是Killing矢量场，并且我们会发现这些矢量场构成线性空间，实际上正是等距同构群在单位处的切空间。这比较容易想象，无穷小逼近就是只移动一点点时用向量去逼近，这里只移动一点点就是几乎不动的意思，而不动的等距同构就是单位元。关于矢量场，天然地就有代数运算李括号，于是得到新的代数结构——李代数。
  李群元素位于微分流形上，那么每一个李群元素处都可以有一个降一维的切空间。那么规定幺元处的切空间就是李代数，其他李群处的就是普通切空间。

2.1李代数定义

  每个李群都有与之对应的李代数。李代数描述了李群的局部性质。其定义为：李代数由一个集合VVV, 一个数域FFF和一个二元运算[,][,][,], 组成。如果它们满足以下几条性质，则称为一个李代数。
  封闭性：∀X,Y∈V,[X,Y]∈V{\forall} X,Y \in V,[X,Y] \in V∀X,Y∈V,[X,Y]∈V
  双线性：∀X,Y,Z∈V,a,b∈F{\forall} X,Y,Z \in V,a,b \in F∀X,Y,Z∈V,a,b∈F，有[aX+bY,Z]=a[X,Z]+b[Y,Z],[Z,aX+bY]=a[X,Z]+b[Y,Z][aX+bY,Z]=a[X,Z]+b[Y,Z],[Z,aX+bY]=a[X,Z]+b[Y,Z][aX+bY,Z]=a[X,Z]+b[Y,Z],[Z,aX+bY]=a[X,Z]+b[Y,Z]
  自反性：∀X∈V,[X,X]=0{\forall} X \in V,[X,X] = 0∀X∈V,[X,X]=0
  雅可比等价：∀X,Y,Z∈V,[X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0{\forall} X,Y,Z \in V,[X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0∀X,Y,Z∈V,[X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0