题目链接：https://leetcode.cn/problems/shun-shi-zhen-da-yin-ju-zhen-lcof/

1. 题目介绍（29. 顺时针打印矩阵）

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

【测试用例】：
示例 1：

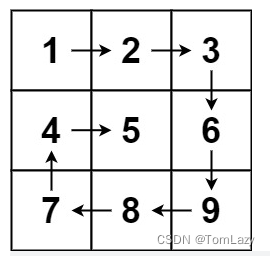
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

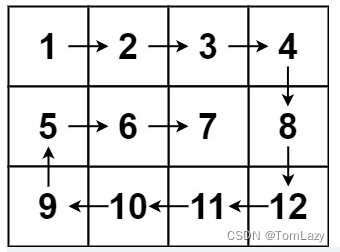
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

【条件约束】：

限制：

• 0 <= matrix.length <= 100
• 0 <= matrix[i].length <= 100

【相关题目】：

注意：本题与主站 54. 螺旋矩阵 题目相同。

2. 题解

2.1 设定边界循环打印（原书题解） – O(mn)

时间复杂度O(mn)，空间复杂度O(mn)

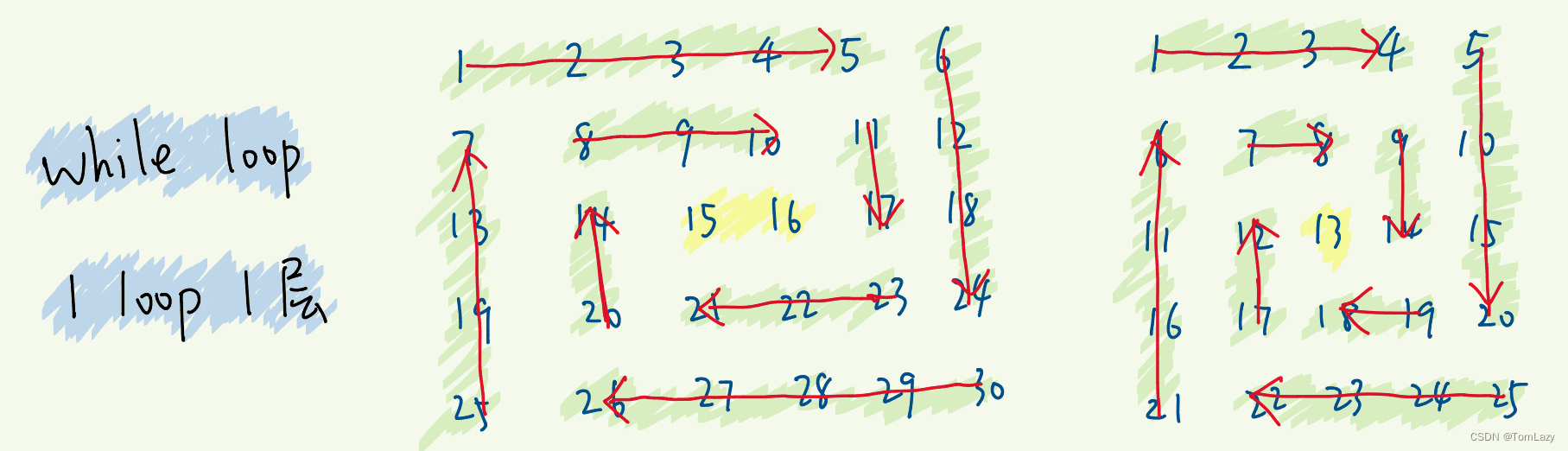
思路：
由于是顺时针打印矩阵，那么就是从外圈到内圈的顺序依次打印，所以我们可以把矩阵想象成若干个圈，利用一个循环来打印矩阵，一次打印矩阵中的一个圈。

• 循环条件：cols > startX * 2 && rows > startY * 2 （这是总结规律发现的，打印第一圈时，左上角的坐标是(0,0)，第二圈的左上角的坐标是(1,1,)，即左上角的坐标中行标和列标总是相同）
• 打印一圈：分为四步（有一点值得注意的是：最后一圈可能会退化不满一圈，它最多只会存在前三步，那么我们就需要根据相关情况，对其进行条件的设置）
  • 第一步：从左到右打印一行（一定会触发）；
  • 第二步：从上到下打印一列（终止行号要大于起始行号）；
  • 第三步：从右到左打印一行（除了终止行号要大于起始行号外，还需要终止列号大于起始列号）；
  • 第四步：从下到上打印一列（要求终止行号比起始行号至少大2，同时终止列号也要大于起始列号）；

class Solution {public int[] spiralOrder(int[][] matrix) {// 判空if(matrix.length == 0) return new int[0];// 定义行数和列数int cols = matrix[0].length;int rows = matrix.length;int start = 0;int index = 0;int[] res = new int[rows * cols];        // 循环打印符合条件的圈while (rows > start * 2 && cols > start * 2){int endX = cols - 1 - start;int endY = rows - 1 - start;// ----->for (int i = start; i <= endX; i++){res[index++] = matrix[start][i];}// ↓if (endY > start){for (int i = start+1; i <= endY; i++){res[index++] = matrix[i][endX];}}// <-----if (endY > start && endX > start){for (int i = endX - 1; i >= start; i--){res[index++] = matrix[endY][i];}}// ↑if (endX > start && endY - 1 > start){for (int i = endY-1; i >= start+1; --i){res[index++] = matrix[i][start];}}start++;}return res;}
}

控制边界的简化解法：

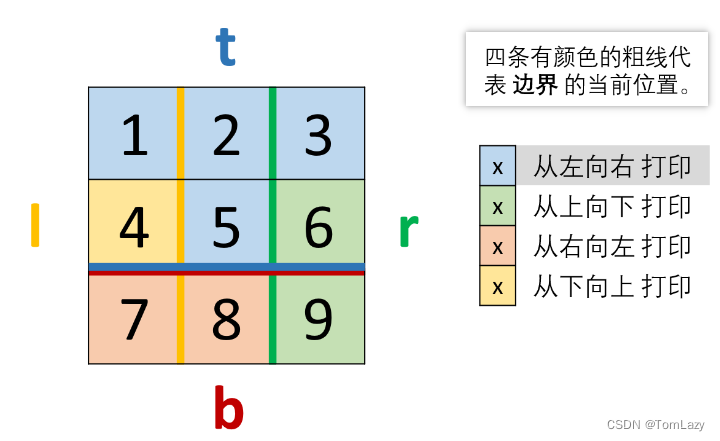
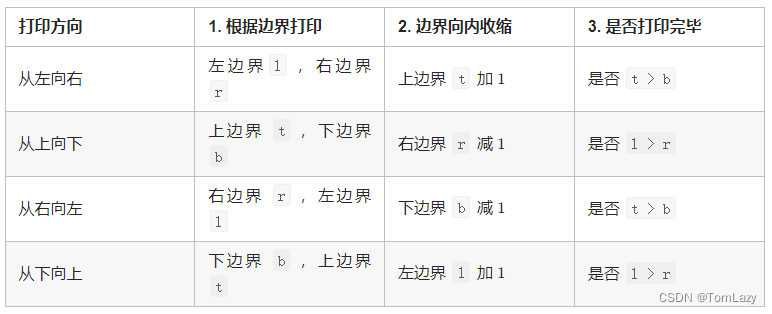
class Solution {public int[] spiralOrder(int[][] matrix) {if(matrix.length == 0) return new int[0];int l = 0, r = matrix[0].length - 1, t = 0, b = matrix.length - 1, x = 0;int[] res = new int[(r + 1) * (b + 1)];while(true) {for(int i = l; i <= r; i++) res[x++] = matrix[t][i]; // left to right.if(++t > b) break;for(int i = t; i <= b; i++) res[x++] = matrix[i][r]; // top to bottom.if(l > --r) break;for(int i = r; i >= l; i--) res[x++] = matrix[b][i]; // right to left.if(t > --b) break;for(int i = b; i >= t; i--) res[x++] = matrix[i][l]; // bottom to top.if(++l > r) break;}return res;}
}

3. 参考资料

[1] 面试题29. 顺时针打印矩阵（模拟、设定边界，清晰图解）-- 2.1 简化解法来源
[2] 「手画图解」两种遍历的策略 – 2.1 开头图片来源