考虑到C站最近的竞赛都在重复以前的旧题，而此题也曾经出现在第9期的比赛里，且有一定难度，很有可能会被再次考到，所以问哥带大家一起复习一遍。 另外问哥发现原贴下面的题解基本都是错的，忍不住想啰嗦几句，奉上此贴，带大家吃透这道题。

题目描述

在河上有一座独木桥，一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子，青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数，我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点：（其中  是桥的长度）。坐标为  的点表示桥的起点，坐标为  的点表示桥的终点。青蛙从桥的起点开始，不停的向终点方向跳跃。一次跳跃的距离是  到  之间的任意正整数（包括 ）。当青蛙跳到或跳过坐标为  的点时，就算青蛙已经跳出了独木桥。

题目给出独木桥的长度 ，青蛙跳跃的距离范围 ，桥上石子的位置。你的任务是确定青蛙要想过河，最少需要踩到的石子数。

输入格式

输入共三行，

• 第一行有 11 个正整数 ，表示独木桥的长度。
• 第二行有 33 个正整数 ，分别表示青蛙一次跳跃的最小距离，最大距离及桥上石子的个数。
• 第三行有  个不同的正整数分别表示这  个石子在数轴上的位置（数据保证桥的起点和终点处没有石子）。所有相邻的整数之间用一个空格隔开。

输出格式

一个整数，表示青蛙过河最少需要踩到的石子数。

输入输出样例

输入

10
2 3 5
2 3 5 6 7

输出

2

说明/提示

【数据范围】

，，

分析

原贴在这里。

本题第一个难点是——理解题意。没错，这是第一个曾让问哥感到郁闷的地方。“你的任务是确定青蛙要想过河，最少需要踩到的石子数”，这里最少需要踩到的石子数，指的是不得不踩到的石子，而不是一定要踩着石子才能过河，比如，青蛙完全可以不踩石子，从石子间的空隙踩着独木桥过去。而青蛙能不能踩到石子，是因为它每次只能跳出  的距离，所以就有可能不管它怎么跳，某些石子就是绕不过去。所以，我们的任务是统计这样的石子有多少。

OK，如果这里没问题，后面就简单了，接下来就是一眼动态规划了。很容易想到，青蛙朝着一个方向跳，不会回头，那么它后面无论选择怎么跳都不会影响已经跳过的石子——无后效性。所以我们可以使用动态规划从起点到终点一步步推导出到达每个位置不得不踩到的石子数，然后在这里边找一条石子数量整体最少的。

比如，我们可以定义  表示为在  点不得不踩到的石子数。那么很显然，要想到达  点，青蛙可以从最远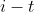的  点、最近的  点跳过来，我们只要检查  到  这些点不得不踩到的最少石子，也就是  中的最小值，然后加上  点本身的状态即可得出要想到达 i 最少要踩到的石子数。如果  点有石子，则结果加1。

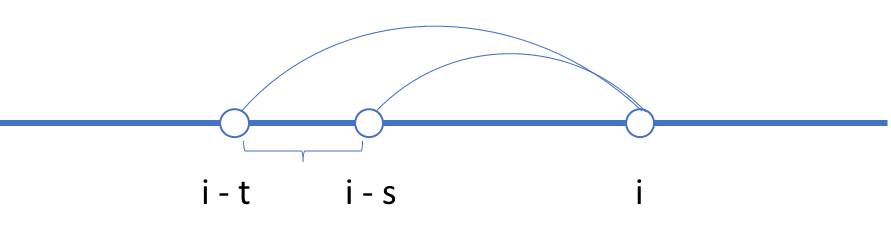
用状态转移方程表达就是：

• 如果位置  有石子，
• 如果位置  不是石子，

本题的整体解题思路就分析完毕了，就是这么简单。

但是仔细一看，就会发现本题真正的坑在于数据范围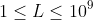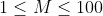：， 。宽到可以容纳 1 亿颗石子的独木桥上，竟然最多只有 100 颗石子。这就意味着桥面上大部分地方都是没有石子的，而我们的状态转移方程却需要每个点都计算一遍。如果某段桥面没有石子，那在这段距离里的大部分点的计算都是对结果没有价值的。所以可以考虑压缩路径，也就是跳过那些对结果状态不产生价值的计算点。一定存在某个距离，在它之外的点，都是无价值的。于是可以把相距超过这个距离的两颗石子，压缩到这个距离，从而省去那些无价值的计算。

到这里，问哥和大部分题解作者的共识是一致的。但是该怎么压缩（或者叫离散化），这个距离是多少，网上各执一词。有说按照 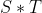 的，有说按照 2520 （1到10的最小公倍数）的，有说按照 90 的，有说按照 71 的，分析了一大堆。但是问哥认为，都没说到点子上，观众也是看得云里雾里、似懂非懂。

其实，这个可压缩到的最小距离，和 （最小公倍数）压根没关系。

我们之所以可以省略这个最小距离之外的那些点，是因为这个距离之后、到下颗石子之前的所有点的状态，都可以由这个距离之内的点（必要的计算点）的状态转移过去。另一方面，我们要求的是一个极值（最少石子数），所以必要的计算点的相对顺序对结果没有影响，只要它们都被计算到即可。

那么这个最小距离是多少呢？答案是  ，或 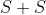（都不关  的事）。

道理其实很简单，假设青蛙站在起点 0（或站在前一颗石子上），那么它最近只能跳到  点，那么，我们在计算  点之后的点的状态时，起点至  点之间的所有点的状态都有被计算到的可能（回想一下我们的状态转移方程）。

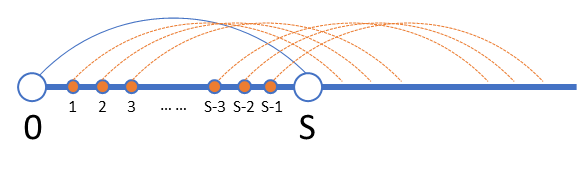
所以，从起点 0 至  点之间的所有点，都是必要的计算点，也就是不可被压缩的。（某种意义上讲也是废话，如果可以压缩到比  还小，就无需计算了）

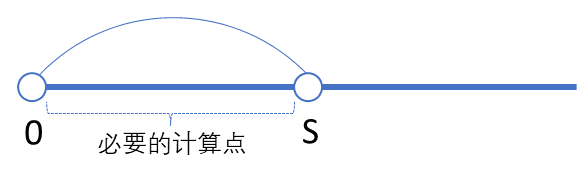
而显而易见地，这些必要的计算点里最远的点的状态会被转移到的最近位置，就是 。

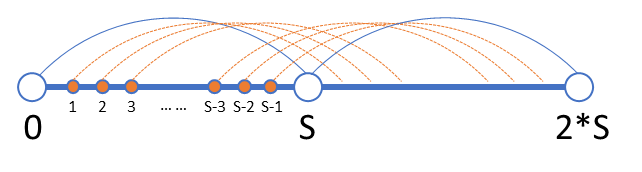
换句话说，在点  的位置，我们就已经考虑到了所有必要计算点的状态，而在这个点及以后的点都可以由  范围内的点的状态转移过去。所以，如果下一颗石子的位置距离起点 0（或上一颗石子）超过 ，就可以直接把它“挪到” ，因为从  到它之间的所有点的计算都是无价值的，也就是说，这段距离是可以被“压缩”的。

是不是很简单呢？

这里还有个极端情况要考虑，那就是当 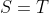 时，青蛙并不能跳到 、、 之间的任何位置，所以无法考虑必要计算点。对于这种情况，我们只要判断石子的位置是不是  的倍数即可，如果是，就不得不踩上这颗石子。

本题最后的计算，还有个小坑，那就是青蛙的最后一跳，可以不用跳在  上，而是只要比这个位置远就可以。所以我们的  数组的最远范围要开到 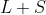，然后最后输出的结果实际上是  到  之间的最小值。

参考代码

L = int(input())
s, t, m = map(int, input().split())
arr = sorted(map(int, input().split()))
if s == t: print(sum(i % s == 0 for i in arr))
else:x = 2*s + 0 # 只要大于等于2*s，随便加个数都能过，比如71,90,2520。。。stones = set()y = min(x, arr[0]) # 起点到第一颗石子的距离如果大于x，就压缩成xstones.add(y)for i in range(1, m):y += min(arr[i] - arr[i-1], x) # 如果两颗石子相距大于x，就压缩成xstones.add(y)L = y + min(L - arr[-1], x) # 最后一颗石子到终点的距离也同样压缩# 开始动态规划转移状态 dp = [float("inf")]*(L + s) # 最后一跳可能超过L，但最远也只需计算到L+Sdp[0] = 0for i in range(1, L + s):for j in range(s, t+1):if i >= j: dp[i] = min(dp[i], dp[i-j] + (i in stones))print(min(dp[L:]))