【动态规划】不同路径,编辑距离题解及代码实现
Halo,这里是Ppeua。平时主要更新C语言,C++,数据结构算法......感兴趣就关注我吧!你定不会失望。
🌈个人主页:主页链接
🌈算法专栏:专栏链接
我会一直往里填充内容哒!
🌈LeetCode专栏:专栏链接
目前在刷初级算法的LeetBook 。若每日一题当中有力所能及的题目,也会当天做完发出
🌈代码仓库:Gitee链接
🌈点击关注=收获更多优质内容🌈
目录
题目:不同路径
题解:
代码实现:
题目:编辑距离
题解:
先来看看跳过
再来看看插入
再来看看删除
最后来看看替换操作:
代码实现:
完结撒花:
两题由简单到难得DP问题!助我们拿下DP!
题目:不同路径
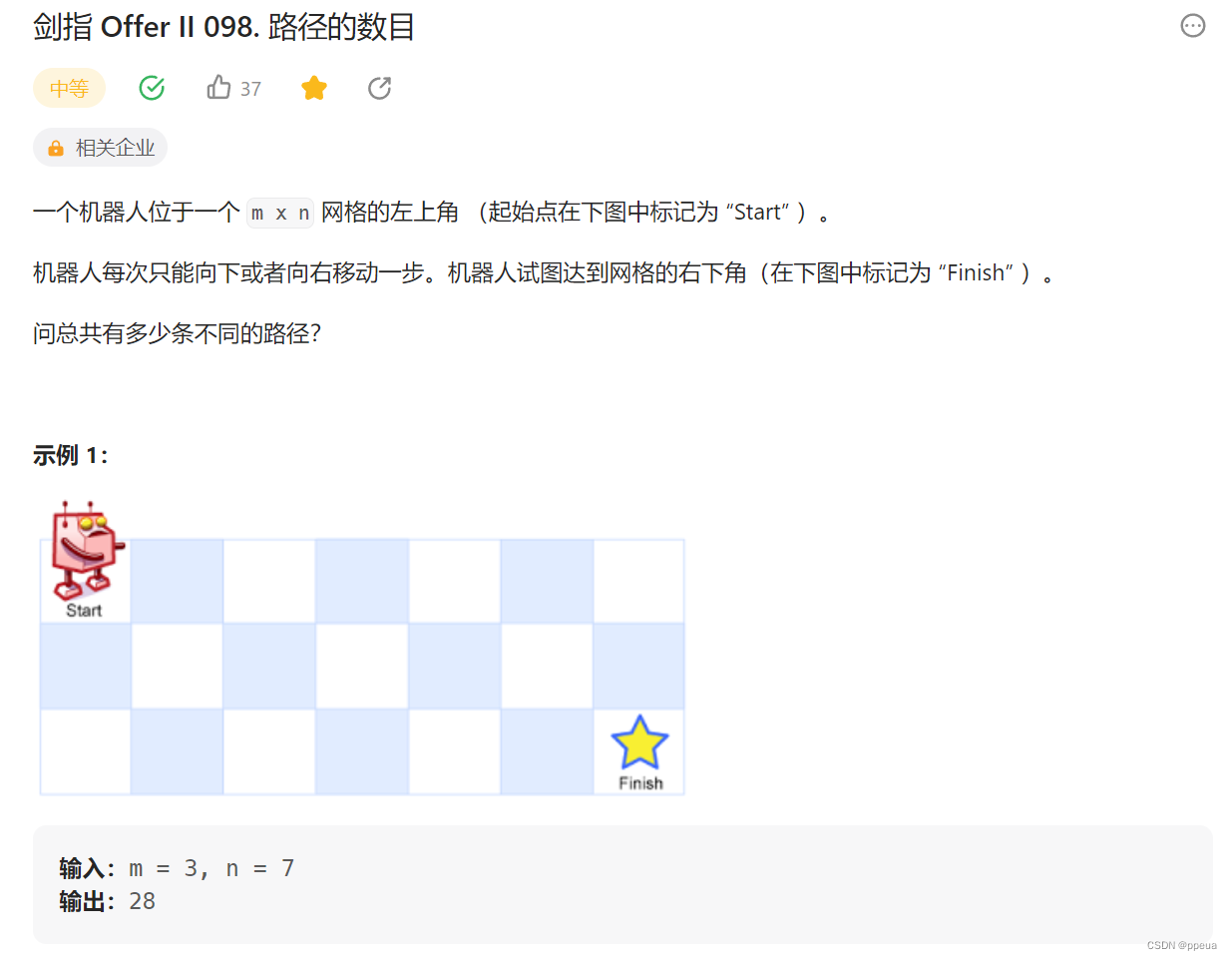
题解:
这题非常的简单,算是动态规划里的入门题了,但我们再来认真复习一下动态规划的内容。
首先明确状态,根据题所给,我们的状态就是dp[i][j]:走到第i行第j列时,有多少种路径。
那我想要走到第i行第j列只能从以下两种方法走到
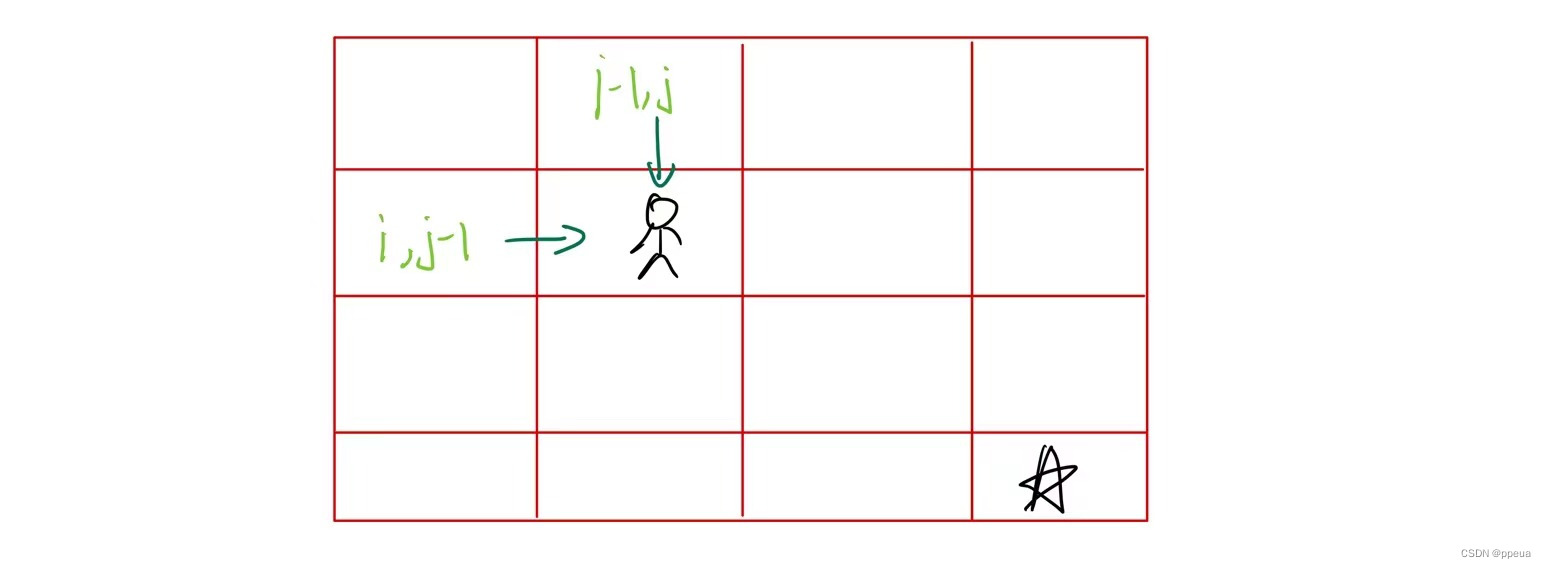
所以状态转移方程就出来了:dp[i][j]=dp[i-1][j]+dp[i][j-1]
那么这道题不就迎刃而解了嘛?
但是,我们还得初始化下初始的情况。
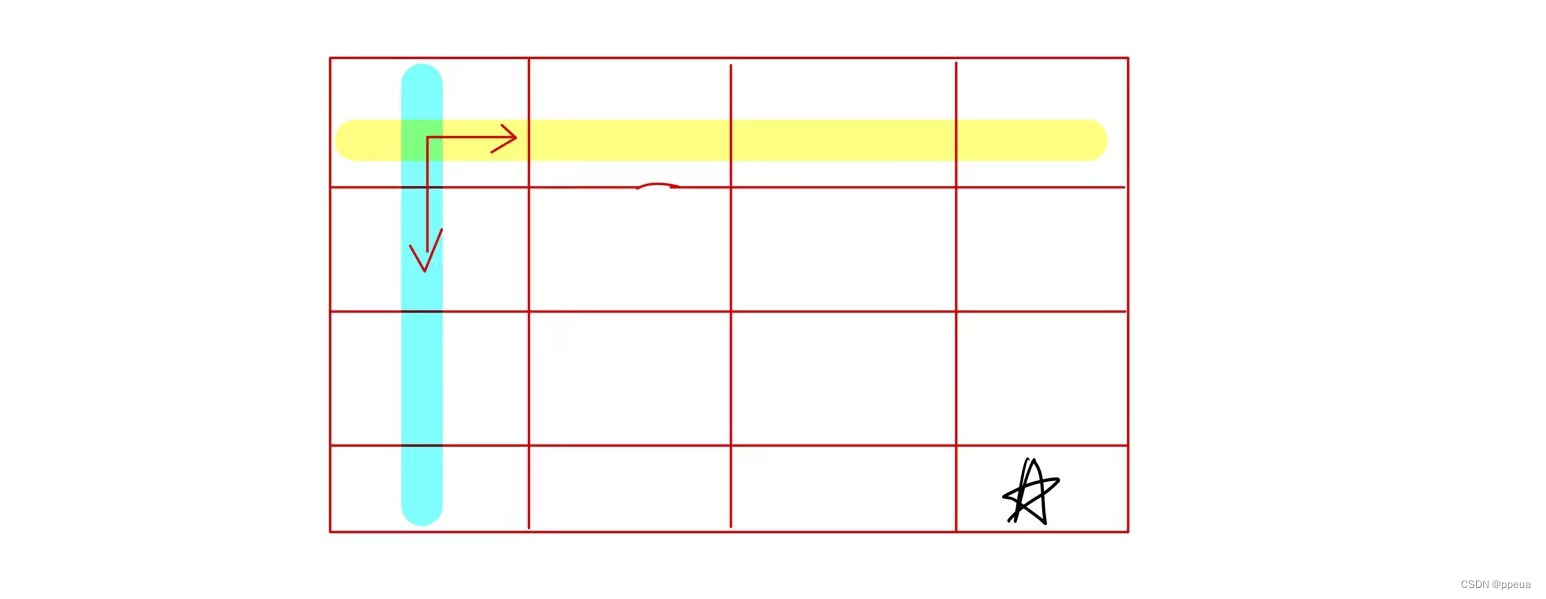
若要走到(0,0)有几条路?显然只有一条
那走到(i,0),与(0,j)呢?也只有一条,因为,只能向右或者向左走,所以将其都初始化为1即可。这样base case也完成了。这题也就结束了。
代码实现:
#include
#include
#include
using namespace std;
class Solution {
public:int uniquePaths(int m, int n) {vector>dp(m,vector(n));dp[0][0]=1;for(int i=0;i 题目:编辑距离
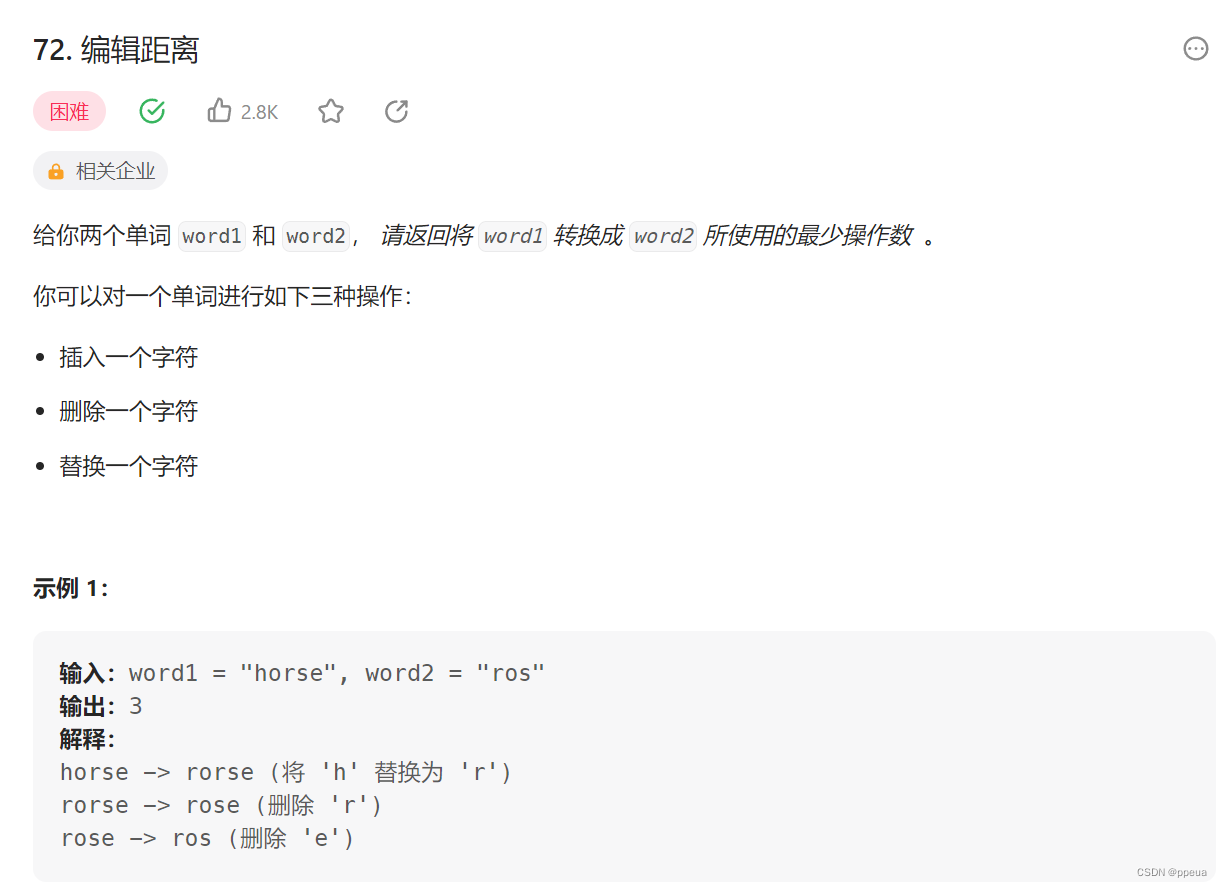
题解:
这题有点困难,但也没有想象中的那么难。仍然跟着三板斧走:状态(dp的含义) 状态转移方程 ,以及base case
首先来分析下题目:
将word1变成word2最短要几步?
那么显而易见,这里的dp状态就是为,将word1的前i个与word2的前j个字母对齐最少 需要几步。
对字符串处理有三种方法:插入删除替换,这里还有一个隐藏的方法,跳过(当两个字符相同的时候就可以执行跳过这一步骤)
先来看看跳过
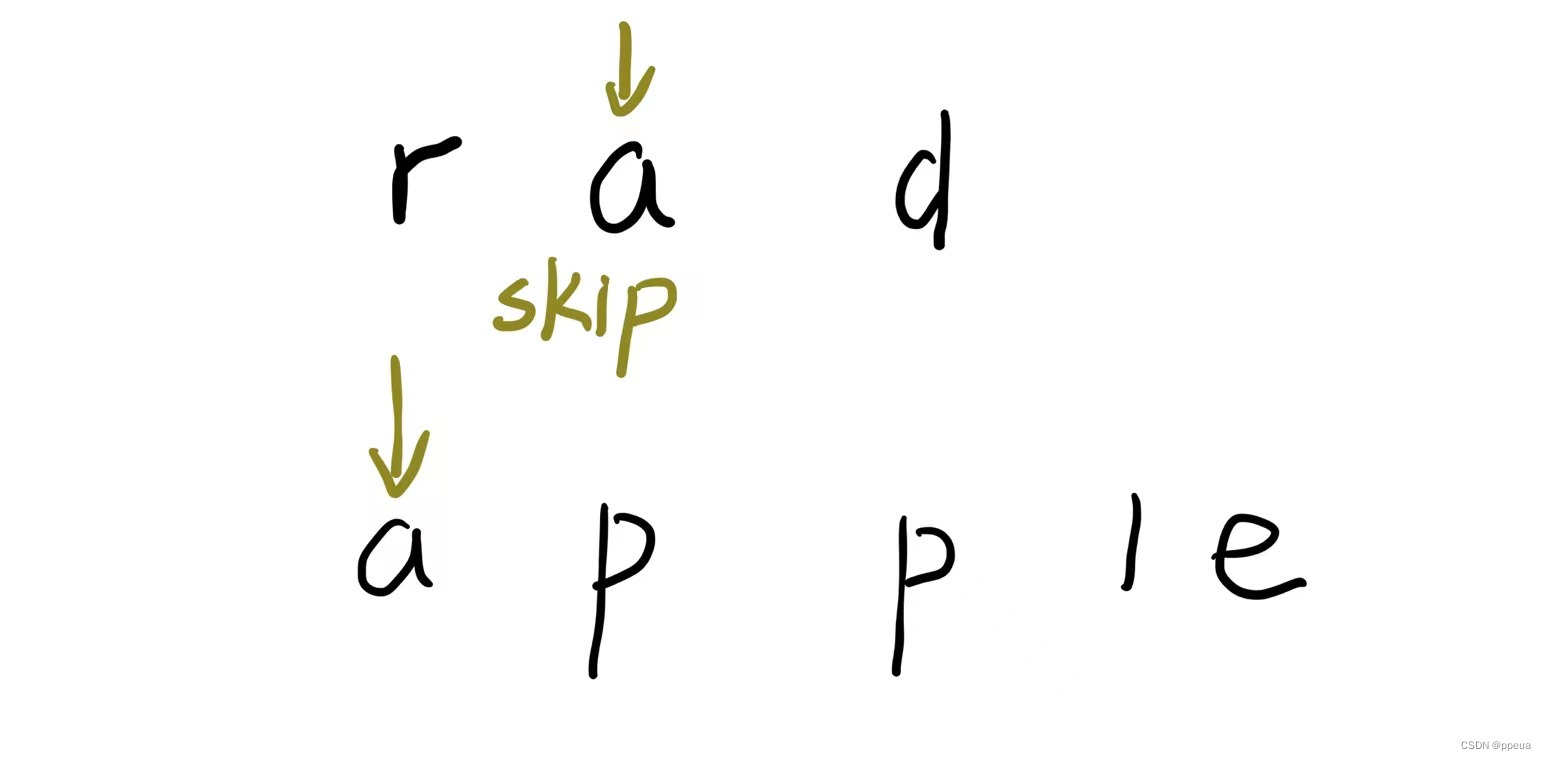
他的情况就是为:当word[i]==word[j]时,操作数就与前一个字母相同,即dp[i][j]=dp[i-1][j-1]
再来看看插入
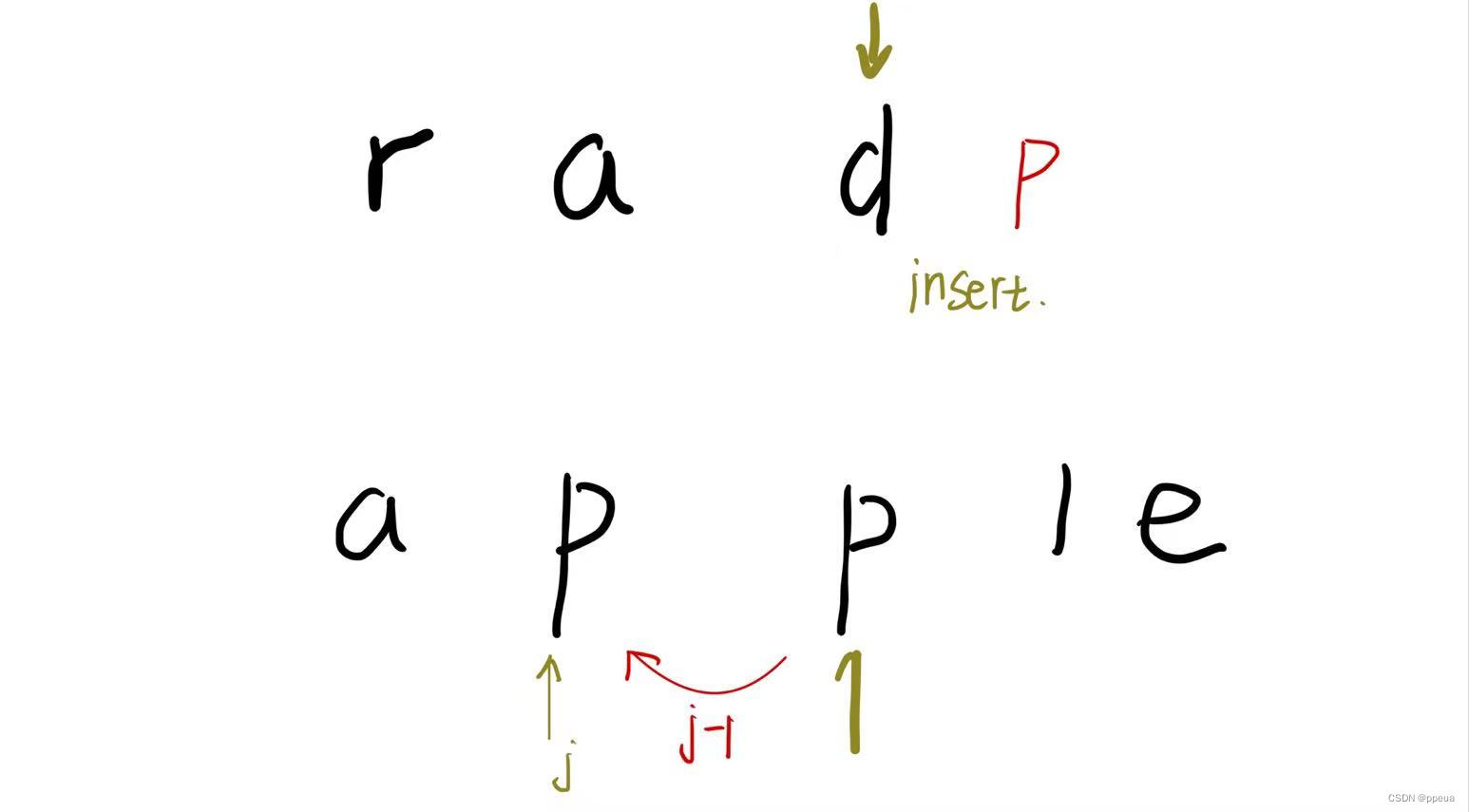
当word1[i]!=word[j]时, 将word[j]插入,此时将word[j]导致的就是,i指向为插入为i+1,与此时的j比较,相等,第一种跳过的情况,所以i=i+1-1也就是i,而j变成了j-1.说了这么多也就是想说,插入的那个字母表示已经比对过了,zhihj往前跳一个与此时的i进行比较即可.(插入是我觉得最难的地方,不懂得uu门可以自己画图理解一下)
所以其dp方程为DP[i][j]=DP[i][j-1]+1
再来看看删除
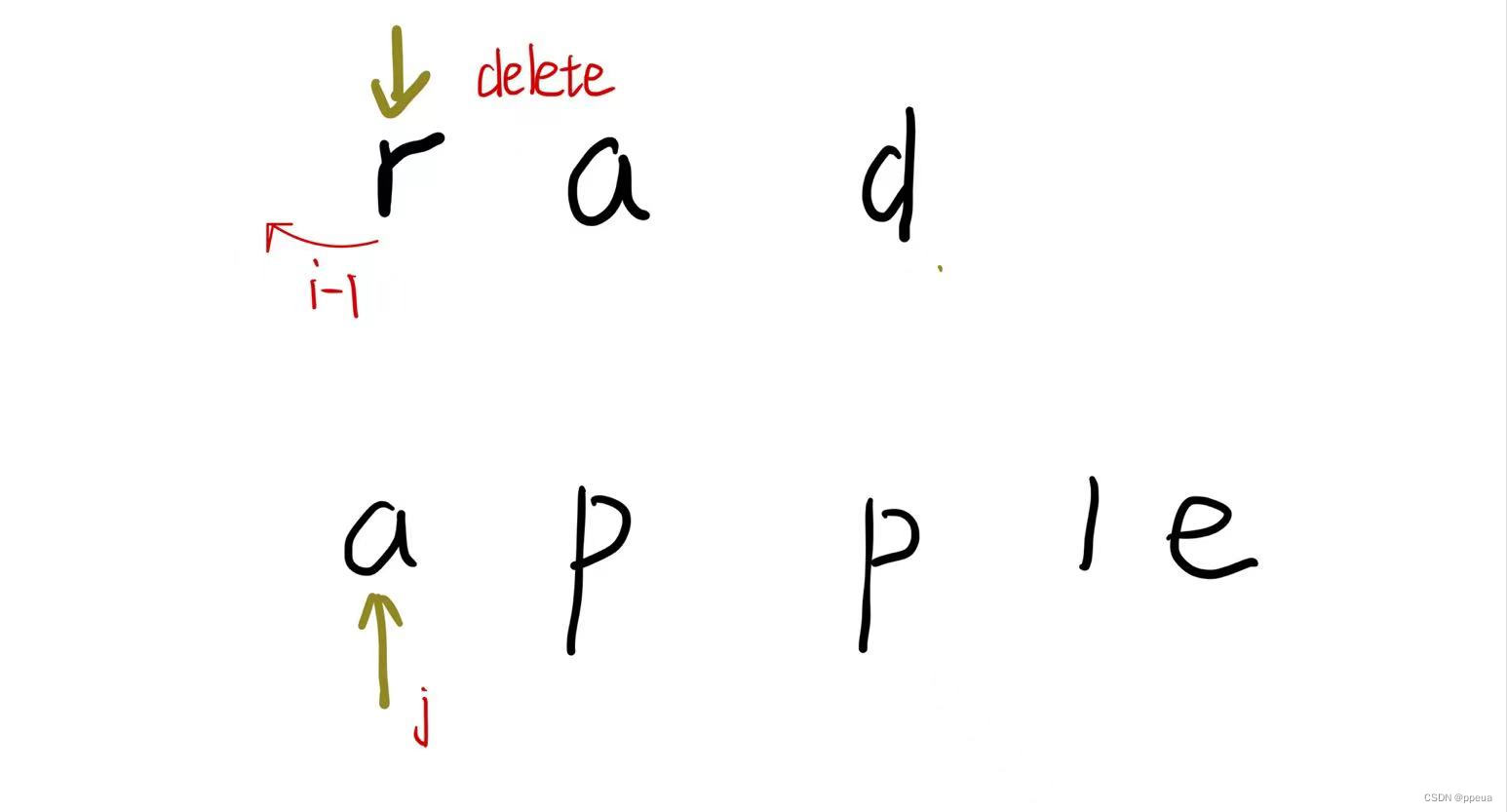
这个就很好理解了,把i指向的字母删掉,操作数加一,之后继续将i-1与j比较.
所以DP方程为:DP[i][j]=DP[i-1][j] +1
最后来看看替换操作:
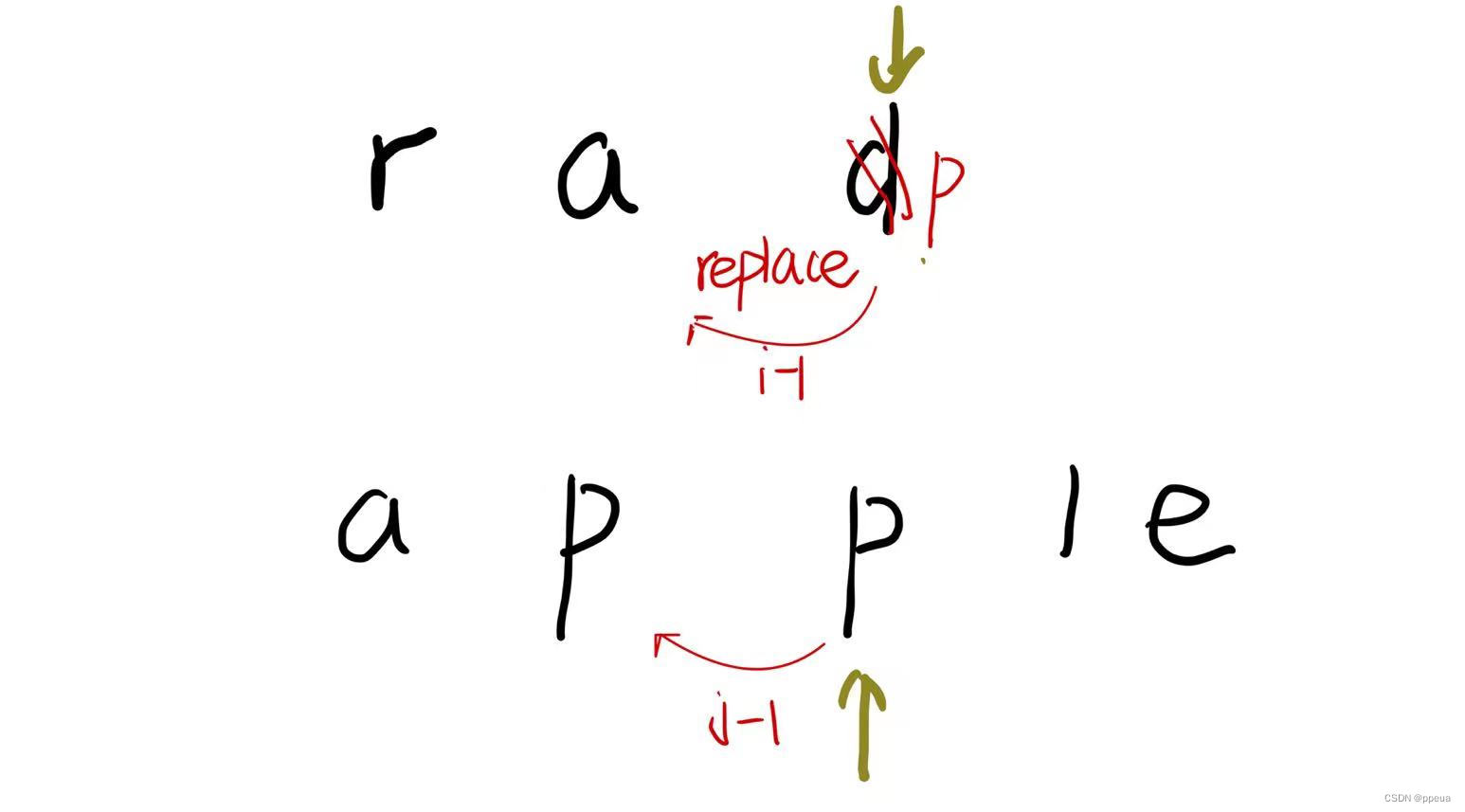
这个和skip有点像,因为他们的DP方程都相同,唯一的区别就在于,操作数是否要加一(替换需要加一,而skip并不需要).
将i指向的字母替换成j指向的字母,替换后两个字母相同,此时执行skip操作即可
所以其dp方程为:DP[i][j]=DP[i-1][j-1]+1
到此四种情况都讲完了,还差最后一板斧,base case;
这里的base case也非常好理解,
当i字符串比j字符串要短的时候,也就是dp[0][j],此时要操作的数目就是插入j个字符,操作数为j,所以dp[0][j]=j
当j字符串比i字符串要短的时候.也就是dp[i][0],此时要操作的数目就是删除i个字符,操作数为i,所以dp[i][0]=i
至此,三板斧已经全部解决完,其实就是若skip情况出现,则用其结果,若没出现,则其他三种一个个试过去找最小的情况.
接下来看看代码中值得注意的地方
代码实现:
#include
#include
#include
#include
using namespace std;
class Solution {
public:int minDistance(string word1, string word2) {vector>dp(word1.size()+1,vector(word2.size()+1));int l1=word1.size();int l2=word2.size();if(l1*l2==0)return l1+l2;for(int i=0;i<=l1;i++)dp[i][0]=i;for(int j=0;j<=l2;j++)dp[0][j]=j;for(int i=1;i<=l1;i++){for(int j=1;j<=l2;j++){//skip情况if(word1[i-1]==word2[j-1])dp[i][j]=dp[i-1][j-1];//dp从1开始,对应的word为-1 //replace delete insert 三者找最小的可能else dp[i][j]=min(dp[i-1][j-1]+1,min(dp[i-1][j]+1,dp[i][j-1]+1));}}return dp[l1][l2];}
}; 完结撒花:
🌈本篇博客的内容【动态规划:不同路径,编辑距离题解及代码实现】已经结束。
🌈若对你有些许帮助,可以点赞、关注、评论支持下博主,你的支持将是我前进路上最大的动力。
🌈若以上内容有任何问题,欢迎在评论区指出。若对以上内容有任何不解,都可私信评论询问。
🌈诸君,山顶见!

