第十一届蓝桥杯(省赛)之平面分割
第十一届蓝桥杯(省赛)之平面分割

分析:
一、直线分割平面
问题:直线怎么放置才能使平面被切分得更多?平行还是相交,很明显,肯定是相交。
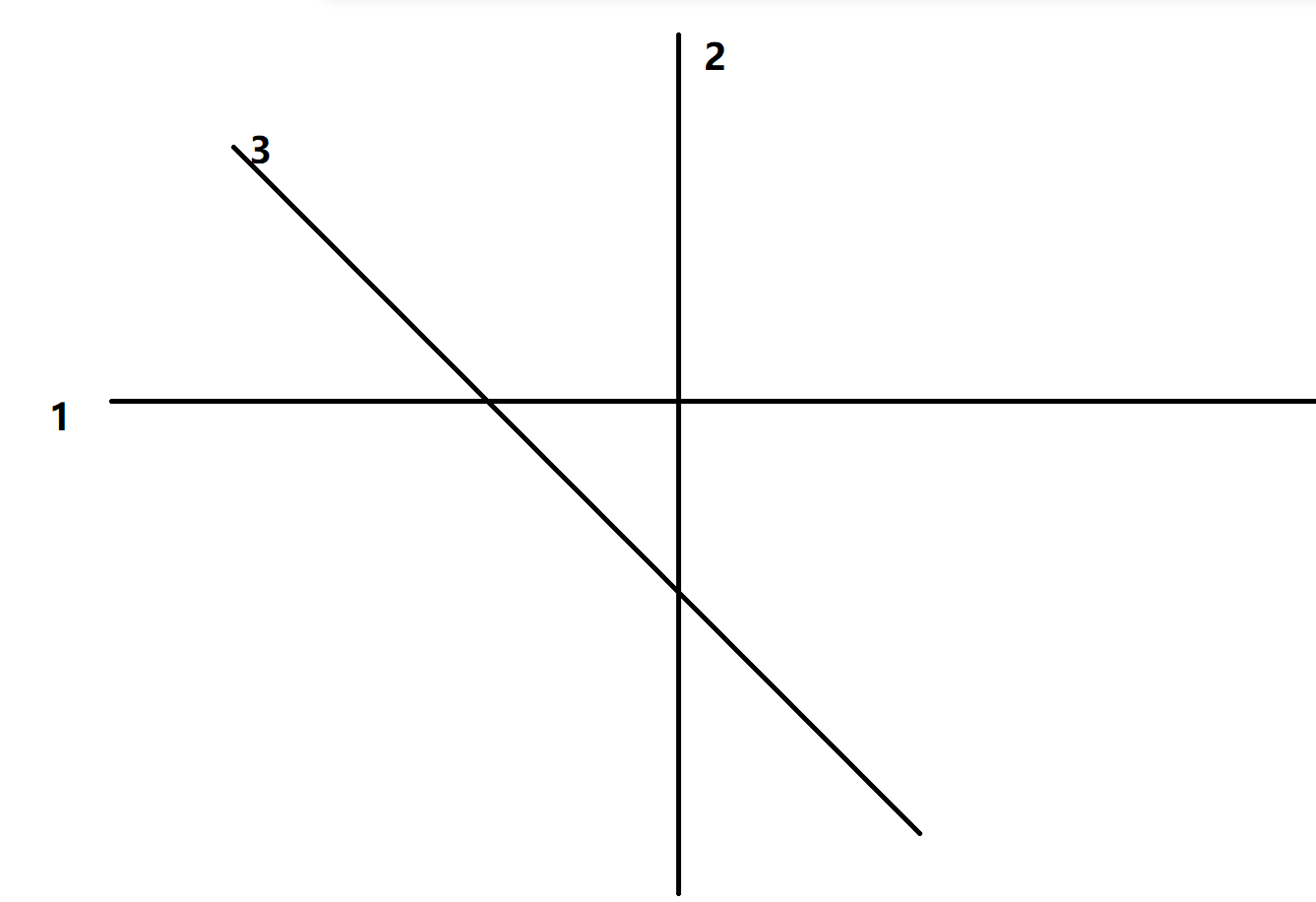
第一条直线将平面分成2份;
第二条直线与前一条直线相交,第二条直线被前 1 条直线分割成 2 份,增加了 2 个平面。
第三条直线与前两条直线相交,第三条直线被前 1 条直线分割成 3 份,增加了 3 个平面。
…
第n条直线与前 n-1 条直线相交,第 n 条直线被分割成 n 份,根据前面的规律可知则新增 n 个平面。
line(n)=line(n−1)+n=line(n−2)+n+n−1=line(n−1)+n+n−1+n−2=...=line(1)+2+3+4+...+n−1+n=2+2+3+4+...+n−1+n=1+(1+n)×n2\begin{aligned} % requires amsmath; align* for no eq. number line(n) & = line(n-1)+n \\ & =line(n-2)+n+n-1\\ & =line(n-1)+n+n-1+n-2\\ & =...\\ & =line(1)+2+3+4+...+n-1+n\\ & =2+2+3+4+...+n-1+n\\ & =1+\frac{(1+n)\times n}{2} \end{aligned} line(n)=line(n−1)+n=line(n−2)+n+n−1=line(n−1)+n+n−1+n−2=...=line(1)+2+3+4+...+n−1+n=2+2+3+4+...+n−1+n=1+2(1+n)×n
二、圆形分割平面
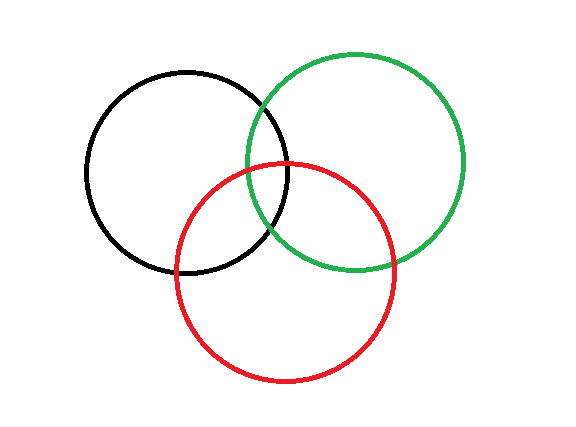
第一个圆将平面分成两份。
第二个圆与前一个圆有 2 个交点,第二个圆被前 1 个圆分成 2 份,平面新增 2 个。
第三个圆与前二个圆有 4 个交点,第三个圆被前 2 个圆分成 4 份,平面新增 4 个。
…
第n个圆与前n-1个圆有 2(n-1) 个交点,第n个圆被前 n-1 个圆分成 2(n-1) 份,平面新增 2(n-1) 个。
round(n)=round(n−1)+2(n−1)=round(n−2)+2(n−2)+2(n−1)=......=round(1)+2+4+...+2(n−2)+2(n−1)=2+2+4+...+2(n−2)+2(n−1)=2+(2+2n−2)×(n−1)2=2+n(n−1)\begin{aligned} % requires amsmath; align* for no eq. number round(n) & = round(n-1) + 2(n-1)\\ & = round(n-2) + 2(n-2) + 2(n-1)\\ & = ......\\ & = round(1) + 2 + 4 + ... + 2(n-2) + 2(n-1)\\ & = 2 + 2 + 4 + ... + 2(n-2) + 2(n-1)\\ & = 2 + \frac{(2+2n-2)\times (n-1)}{2}\\ & = 2 + n(n-1) \end{aligned} round(n)=round(n−1)+2(n−1)=round(n−2)+2(n−2)+2(n−1)=......=round(1)+2+4+...+2(n−2)+2(n−1)=2+2+4+...+2(n−2)+2(n−1)=2+2(2+2n−2)×(n−1)=2+n(n−1)
三、20个圆和20条直线
g(m,n)g(m,n)g(m,n):代表mmm个圆和nnn条直线最多能将平面分割的份数
1、mmm个圆和0条直线
g(m,0)=round(m)=2+m(m−1)\begin{aligned} % requires amsmath; align* for no eq. number g(m,0) & = round(m)\\ & = 2 + m(m-1) \end{aligned} g(m,0)=round(m)=2+m(m−1)
2、mmm个圆和1条直线
直线与圆(不考虑直线与直线)
一个圆将平面切分成 2 份。
第一条直线与圆相交有 2 个交点,直线被圆分成 3 份,新增 2 个平面。
第两条直线与圆相交有 2 个交点,直线被圆分成 3 份,新增 2 个平面。
…
第n条直线与圆相交有 2 个交点,直线被圆分成 3 份,新增 2 个平面。
g(m,1)=g(m,0)+2m\begin{aligned} % requires amsmath; align* for no eq. number g(m,1) & = g(m,0) + 2m \end{aligned} g(m,1)=g(m,0)+2m
3、mmm个圆和2条直线
g(m,2)=g(m,1)+2m+2\begin{aligned} % requires amsmath; align* for no eq. number g(m,2) & = g(m,1) + 2m + 2 \end{aligned} g(m,2)=g(m,1)+2m+2
…
n、mmm个圆和nnn条直线
g(m,n)=g(m,n−1)+2m+n=g(m,n−2)+(2m+n)+(2m+n−1)=g(m,n−3)+(2m+n)+(2m+n−1)+(2m+n−2)=......=g(m,1)+(2m+n)+(2m+n−1)+(2m+n−2)+...+(2m+2)=g(m,0)+(2m+n)+(2m+n−1)+(2m+n−2)+...+(2m+2)+2m=1+m(m−1)+2mn+n(1+n)2\begin{aligned} % requires amsmath; align* for no eq. number g(m,n) & = g(m,n-1) + 2m + n\\ & = g(m,n-2) + (2m + n)+ (2m + n-1)\\ & = g(m,n-3) + (2m + n) + (2m + n-1) + (2m + n - 2)\\ & = ......\\ & = g(m,1) + (2m + n) + (2m + n-1) + (2m + n - 2) + ...+ (2m + 2)\\ & = g(m,0) + (2m + n) + (2m + n-1) + (2m + n - 2) + ...+ (2m + 2) + 2m\\ & = 1 + m(m-1) + 2mn +\frac{n(1+n)} {2} \end{aligned} g(m,n)=g(m,n−1)+2m+n=g(m,n−2)+(2m+n)+(2m+n−1)=g(m,n−3)+(2m+n)+(2m+n−1)+(2m+n−2)=......=g(m,1)+(2m+n)+(2m+n−1)+(2m+n−2)+...+(2m+2)=g(m,0)+(2m+n)+(2m+n−1)+(2m+n−2)+...+(2m+2)+2m=1+m(m−1)+2mn+2n(1+n)
参考文献
[1]蓝桥杯2020初赛 平面分割及相关知识点补充
[2]蓝桥杯真题:平面分割
