1.题目描述

设计求不规则区域周长和面积计算的算法。

测试数据的获得：
输入样例：若干点坐标，从文件读入。
输出样例：面积、周长值
（1）样例 1（凸多边形）输入：
164.5637 62.0682
269.0362 88.6151
288.1998 187.3943
141.6910 223.8191
34.7458 178.1338
60.7094 99.1104
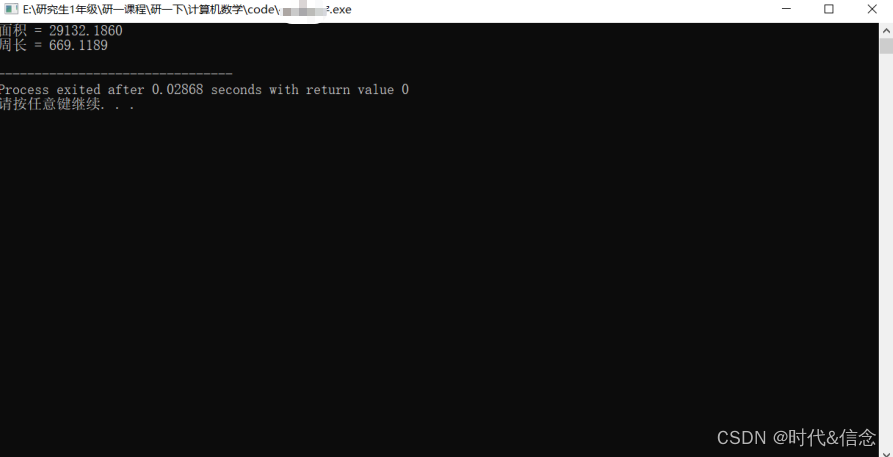
输出：
面积 = 29132.1904，周长 = 669.1189
（2）样例 2（凹多边形）输入：
150.0000 150.0000
60.7094 99.1104
164.5637 62.0682
269.0362 88.6151
288.1998 187.3943
141.6910 223.8191
输出：
面积 = 20806.4298，周长 = 646.704

2.实现思路

（1）计算不规则区域面积

通过向量叉积来实现的。在二维平面上，可以将不规则区域看作由一些线段组成的简单多边形，其面积可以表示为这些线段所构成的向量的叉积之和的绝对值的一半。
具体地，假设不规则区域由n条线段构成，线段的两个端点分别为(x1, y1)和(x2, y2)，则线段的向量为(x2 - x1, y2 - y1)。这些向量的叉积可以表示为：

最后，将上式的结果除以2，即可得到不规则区域的面积。

（2）计算不规则区域的周长

遍历每一个点，使用两点之间距离公式：

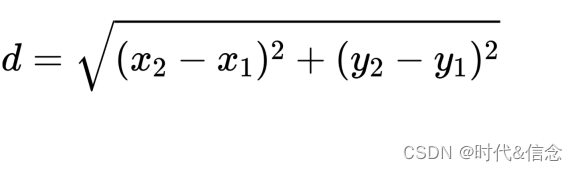
计算相邻两个点之间的距离，使用int j = (i+1) % num_points;加一然后取余的操作，将整个不规则区域连接起来。这样就将不规则区域的各个边的长度计算了出来，最后求和，就是不规则区域的周长。

3.代码

#include 
#include #define MAX_POINTS 1000 // 最大点数typedef struct {double x, y;
} Point; // 点的结构体Point points[MAX_POINTS]; // 点的数组
int num_points = 0; // 点的数量double dist(Point p1, Point p2) 
{// 计算两个点之间的距离double dx = p1.x - p2.x;double dy = p1.y - p2.y;return sqrt(dx*dx + dy*dy);
}double area() 
{// 计算多边形的面积double a = 0;for (int i = 0; i < num_points; i++) {int j = (i+1) % num_points;a += points[i].x * points[j].y - points[j].x * points[i].y;}return fabs(a) / 2;
}double perimeter() 
{// 计算多边形的周长double p = 0;for (int i = 0; i < num_points; i++) {int j = (i+1) % num_points;p += dist(points[i], points[j]);}return p;
}int main() 
{// 从文件中读入点的坐标FILE *fp = fopen("points2.txt", "r");while (fscanf(fp, "%lf%lf", &points[num_points].x, &points[num_points].y) == 2) {num_points++;}fclose(fp);// 计算多边形的面积和周长double a = area();double p = perimeter();// 输出结果printf("面积 = %.4lf\n", a);printf("周长 = %.4lf\n", p);return 0;
}

4.运行结果