傅里叶变换

基本概念

从时域到频域的变换

缺点

对非平稳过程，傅里叶变换有局限性

详解

看如下一个简单的信号：

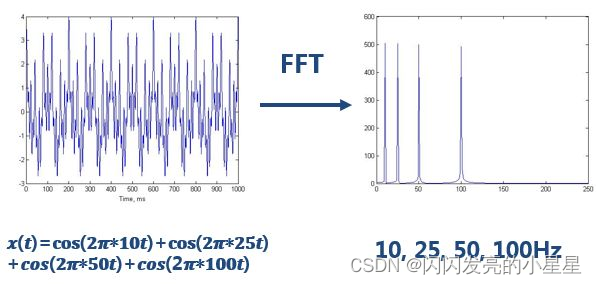
做完FFT（快速傅里叶变换）后，可以在频谱上看到清晰的四条线，信号包含四个频率成分。

一切没有问题。但是，如果是频率随着时间变化的非平稳信号呢？

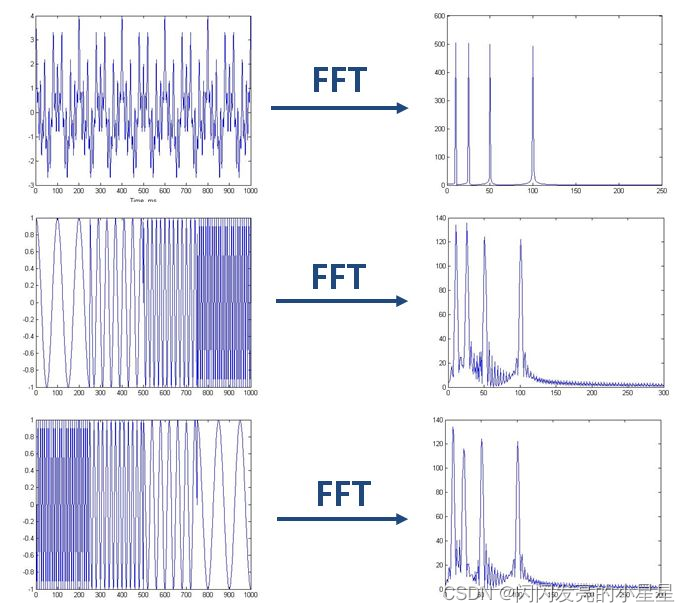
如上图，最上边的是频率始终不变的平稳信号。而下边两个则是频率随着时间改变的非平稳信号，它们同样包含和最上信号相同频率的四个成分。
做FFT后，我们发现这三个时域上有巨大差异的信号，频谱（幅值谱）却非常一致。尤其是下边两个非平稳信号，我们从频谱上无法区分它们，因为它们包含的四个频率的信号的成分确实是一样的，只是出现的先后顺序不同。

可见，傅里叶变换处理非平稳信号有天生缺陷。它只能获取一段信号总体上包含哪些频率的成分，但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号，可能频谱图一样。

然而平稳信号大多是人为制造出来的，自然界的大量信号几乎都是非平稳的，所以在比如生物医学信号分析等领域的论文中，基本看不到单纯傅里叶变换这样naive的方法。

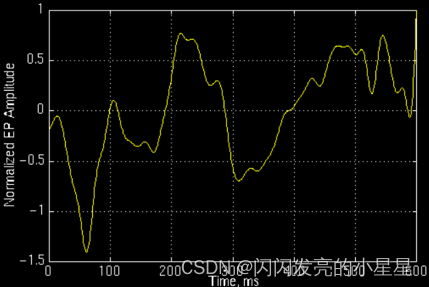
上图所示的是一个正常人的事件相关电位。对于这样的非平稳信号，只知道包含哪些频率成分是不够的，我们还想知道各个成分出现的时间。知道信号频率随时间变化的情况，各个时刻的瞬时频率及其幅值——这也就是时频分析。

python实现：

主要代码：

# 2. 定义FFT函数
def fftanalysis(s,Fs):# fft分析 L = len(s)f = np.arange(int(L / 2)) * Fs / LM = np.abs(fft(s)) * 2 / LM = M[0 : int(L / 2)]M[0] = M[0] / 2return f,M

案例试用：

"""python 中的FFT快速傅里叶分析2023-03-15
"""import numpy as np
from scipy.fftpack import fft
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['KaiTi']
# 1. 生成信号做FFT
FS = 1000  # 采样频率
f1 = 390   # 信号频率1
f2 = 480   # 信号频率2
t = np.linspace(0,1,FS)  # 生成1s的时间序列
noise1 = np.random.random(1000)
y = 2*np.sin(2*np.pi*f1*t)+5*np.sin(2*np.pi*f2*t)+noise1# 2. 定义FFT函数
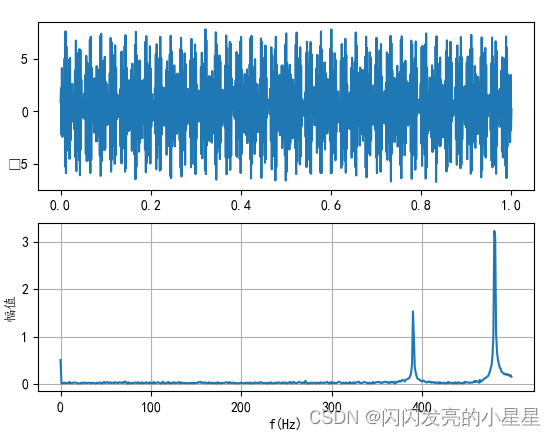
def fftanalysis(s,Fs):# fft分析L = len(s)f = np.arange(int(L / 2)) * Fs / LM = np.abs(fft(s)) * 2 / LM = M[0 : int(L / 2)]M[0] = M[0] / 2return f,MFre,Amplitude = fftanalysis(y,FS)
plt.figure
plt.xticks(range(0,len(t),100))
plt.subplot(2,1,1)
plt.plot(t,y)plt.subplot(2,1,2)
plt.plot(Fre,Amplitude)
plt.xticks(np.arange(0,len(Fre),100))
plt.xlabel("f(Hz)")
plt.ylabel("幅值")
plt.grid()
plt.show()

参考：https://zhuanlan.zhihu.com/p/22450818
https://blog.csdn.net/weixin_43427480/article/details/109138499