860.柠檬水找零

题目链接
思路：
情况一：账单是5，直接收下。
情况二：账单是10，消耗一个5，增加一个10
情况三：账单是20，优先消耗一个10和一个5，如果不够，再消耗三个5

class Solution {
public:bool lemonadeChange(vector& bills) {int five = 0, ten = 0, twenty = 0;for (auto bill : bills) {if (bill == 5) {five++;}if (bill == 10) {if (five == 0) return false;else {five--;ten++;}}if (bill == 20) {// 有10 没 5if (ten >= 1 && five >= 1) {ten--;five--;}//没10 5 >3else if (ten == 0 && five >= 3) {five -= 3;}else {return false;}}}return true;}
};

总结：难度不大，需要静下心来完成，思考每种情况，就很容易解决这道题。

406.根据身高重建队列

题目链接

**思路：**和分发糖果那道题类似，先进行一个维度上的排列，再对另一个维度进行排序。
首先对身高进行排序，从大到小排序，然后再对前面有几个进行选择插入。这里就要实现一个比较的方法，实现这个效果。

class Solution {
public:static bool cmp(vector &a, vector &b) {if (a[0] == b[0]) return a[1] < b[1];return a[0] > b[0];}vector> reconstructQueue(vector>& people) {sort(people.begin(), people.end(), cmp);vector> que;for (int i = 0; i < people.size(); i++) {int pos = people[i][1];que.insert(que.begin() + pos, people[i]);}return que;}
};

明显看是使用C++中的list（底层链表实现）比vector（数组）效率高得多。对使用某一种语言容器的使用，特性的选择都会不同程度上影响效率。

// 版本二
class Solution {
public:// 身高从大到小排（身高相同k小的站前面）static bool cmp(const vector& a, const vector& b) {if (a[0] == b[0]) return a[1] < b[1];return a[0] > b[0];}vector> reconstructQueue(vector>& people) {sort (people.begin(), people.end(), cmp);list> que; // list底层是链表实现，插入效率比vector高的多for (int i = 0; i < people.size(); i++) {int position = people[i][1]; // 插入到下标为position的位置std::list>::iterator it = que.begin();while (position--) { // 寻找在插入位置it++;}que.insert(it, people[i]);}return vector>(que.begin(), que.end());}
};

452. 用最少数量的箭引爆气球

题目链接

思路： 题目读起来很难受，但是实际做起来还是挺简单的。
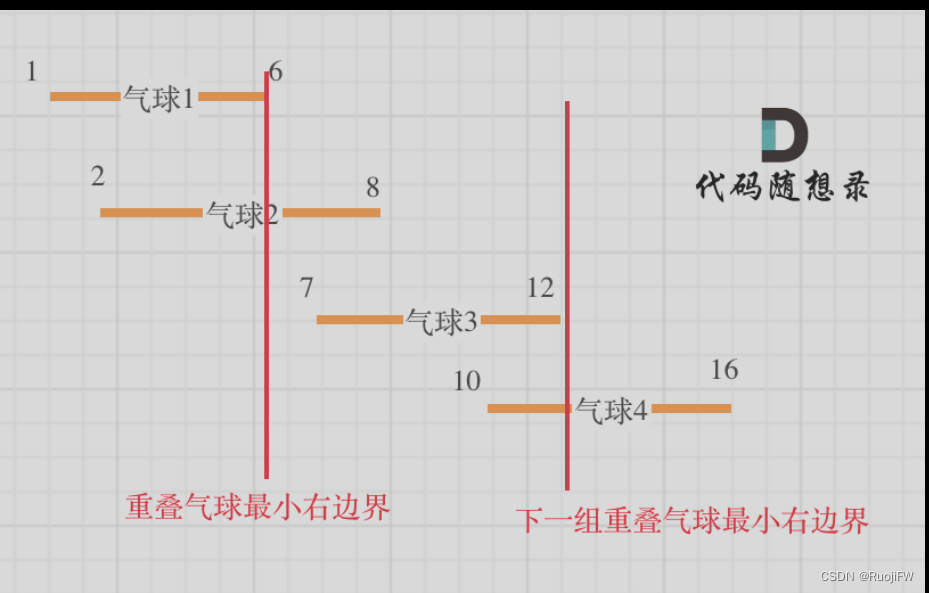
首先对气球的左边界进行从小到大的排序，然后如下图所示。接着遍历数组，对当前气球的右边界和上一个气球的左边界进行比较，如果一家超过了，那么一定需要一根箭，当重叠的时候，降新的用于判断的边界换成重叠时候最小的边界，继续下一轮判断。

class Solution {
private:static bool cmp(const vector& a, const vector& b) {return a[0] < b[0];}
public:int findMinArrowShots(vector>& points) {if (points.size() == 0) return 0;sort(points.begin(), points.end(), cmp);int result = 1; // points 不为空至少需要一支箭for (int i = 1; i < points.size(); i++) {if (points[i][0] > points[i - 1][1]) {  // 气球i和气球i-1不挨着，注意这里不是>=result++; // 需要一支箭}else {  // 气球i和气球i-1挨着points[i][1] = min(points[i - 1][1], points[i][1]); // 更新重叠气球最小右边界}}return result;}
};

**总结：**理解起来很容易，但是自己想的时候感觉不容易想，不过边界排序这部分很熟悉了。