目录

概念

结构

插入 

旋转分类

左旋

右旋

左右双旋

右左双旋

 AVL树验证

AVL树删除

AVL树的性能 

概念

AVL树是一种二叉平衡搜索树，它解决了二叉搜索树退化单枝的问题。 

AVL树的左右子树都是AVL树。

左右子树高度之差(简称平衡因子)的绝对值不超过1。

结构

 AVL树采用三叉链结构，增加了平衡因子bf，通过平衡因子的更新我们对AVL树进行调整，使其保持平衡。

template
struct AVLTNode
{AVLTNode* _left;AVLTNode* _right;AVLTNode* _parent;pair _kv;int bf;AVLTNode(const pair& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),bf(0){}
};
template
class AVLTree
{typedef AVLTNode Node;
private:Node* _root;
}

插入 

插入分为两步：

1.按二叉搜索树规则插入

2.调节平衡因子，在右子树插入，则bf++，在左子树插入，则bf-- 

• 1.parent->bf==0 此时不需要调整
• 2.parent->bf==-1或parent->bf==1,此时需要继续向上调整
• 3.parent->bf==2或parent->bf==-2,此时要进行旋转 

bool Insert(const pair& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;//找空节点while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}//插入节点cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}//调节平衡因子while (parent){if (parent->_left == cur){parent->bf--;}else{parent->bf++;}//无需调整if (parent->bf == 0){break;}else if (parent->bf == -1 || parent->bf == 1){//继续向上调整cur = parent;parent = parent->_parent;}else if (parent->bf == -2 || parent->bf == 2){//开始旋转，旋转后退出//单纯左边高，右旋if (parent->bf == -2 && cur->bf == -1){RoateR(parent);}//单纯右边高，左旋else if (parent->bf == 2 && cur->bf == 1){RoateL(parent);}//左边高， 左右双旋else if (parent->bf == -2 && cur->bf == 1){RoateRL(parent);}//右边高，右左双旋else if (parent->bf == 2 && cur->bf == -1){RoateRL(parent);}break;}else{assert(false);}}return true;}

旋转分类

左旋

单纯右边高，此时进行左旋 

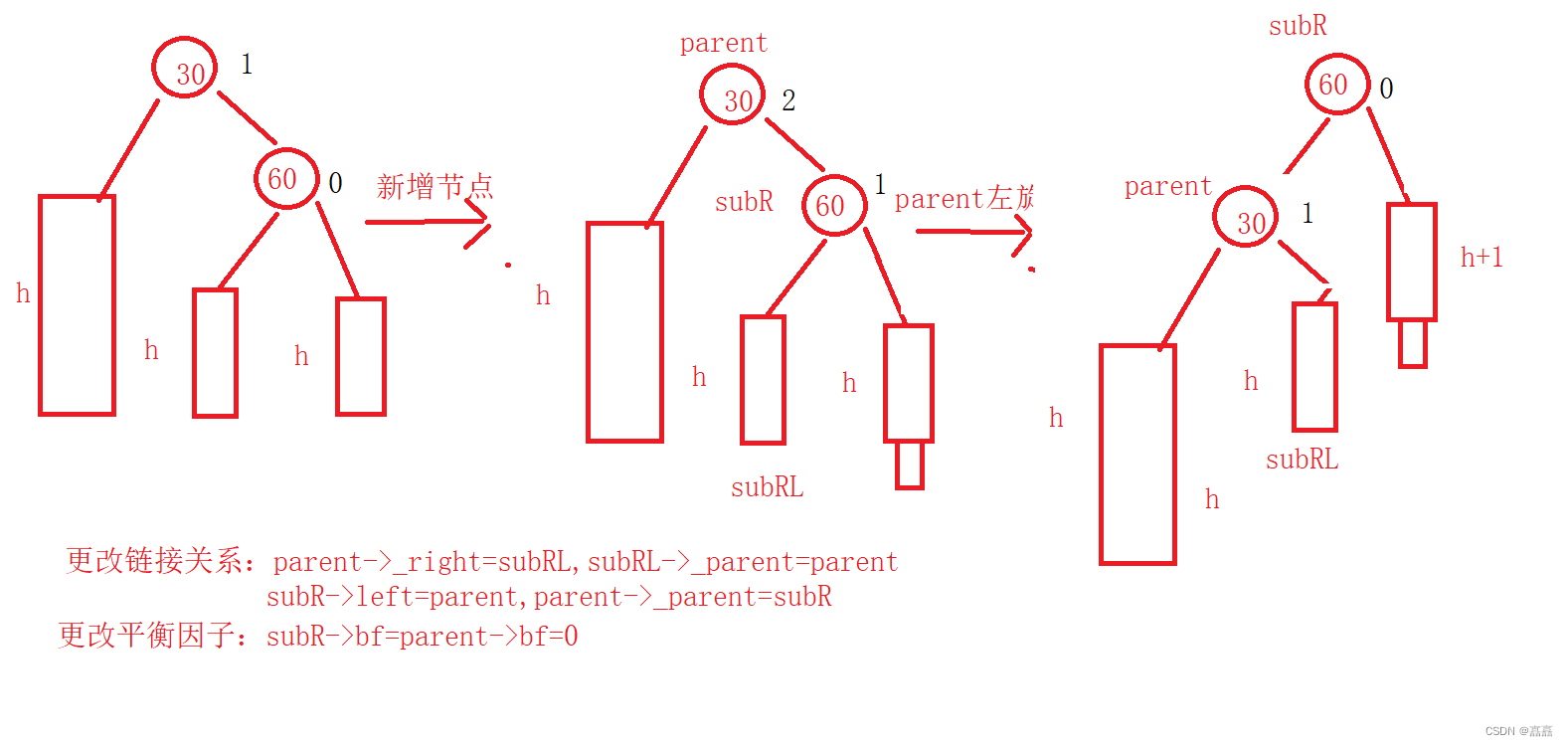
void RoateL(Node* parent){//更改链接关系Node* parentparent = parent->_parent;Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL){subRL->_parent = parent;}subR->_left = parent;parent->_parent = subR;if (parentparent == nullptr){_root = subR;subR->_parent = nullptr;}else{if (parentparent->_left == parent){parentparent->_left = subR;subR->_parent = parentparent;}else{parentparent->_right = subR;subR->_parent = parentparent;}}//调节平衡因子parent->bf = 0;subR->bf = 0;}

右旋

单纯左边高，此时进行右旋 

void RoateR(Node* parent){//更改链接关系Node* parentparent = parent->_parent;Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}subL->_right = parent;parent->_parent = subL;if (parentparent == nullptr){_root = subL;subL->_parent = nullptr;}else{if (parentparent->_left == parent){parentparent->_left = subL;subL->_parent = parentparent;}else{parentparent->_right = subL;subL->_parent = parentparent;}}//调节平衡因子parent->bf = 0;subL->bf = 0;}

左右双旋

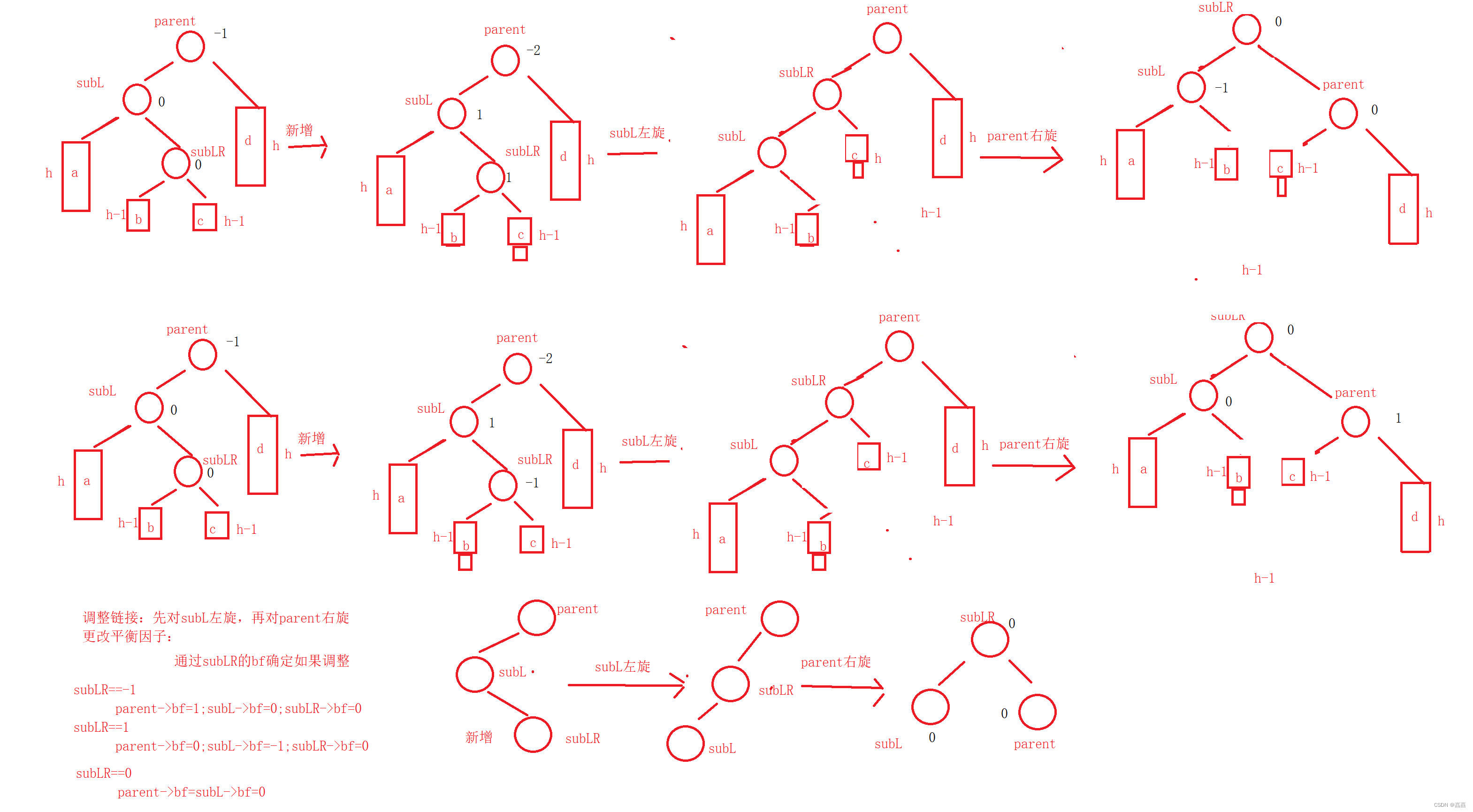
void RoateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->bf;RoateL(subL);RoateR(parent);//调节平衡因子if (bf == 0){parent->bf = 0;subL->bf = 0;}else if (bf == -1){parent->bf = 1;subL->bf = 0;subLR->bf = 0;}else if(bf == 1){parent->bf = 0;subL->bf = -1;subLR->bf = 0;}else{assert(false);}}

右左双旋

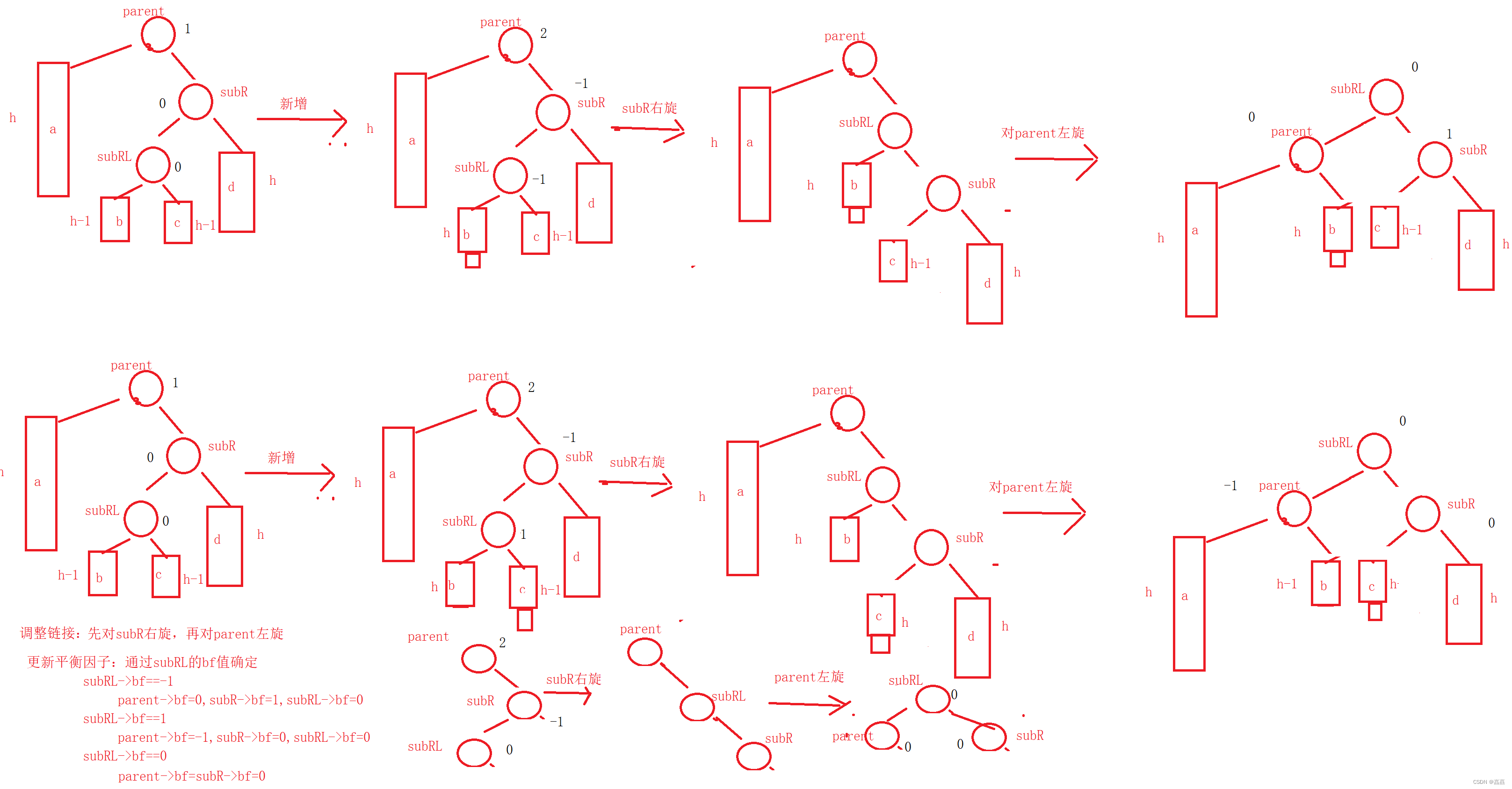
void RoateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->bf;RoateR(subR);RoateL(parent);if (bf == 0){parent->bf = 0;subR->bf = 0;}else if (bf == -1){parent->bf = 0;subR->bf = 1;subRL->bf = 0;}else if(bf == 1){parent->bf = -1;subR->bf = 0;subRL->bf = 0;}else{assert(false);}}

 AVL树验证

如果验证是否是AVL树？

1.先对当前节点求出左右子树高度差，与平衡因子比较是否相等，并确定高度差绝对值是否小于2 

2. 验证左子树是否平衡，验证右子树是否平衡

int Height(Node* root){if (root == nullptr){return 0;}int lefth = Height(root->_left);int righth = Height(root->_right);return lefth > righth ? lefth + 1 : righth + 1;}bool isBanlance(){return _isBanlance(_root);}bool _isBanlance(Node* root){if (root == nullptr){return true;}int left = Height(root->_left);int right = Height(root->_right);if ((right-left) != root->bf){cout << root->_kv.first << "现在是:" << root->bf << endl;cout << root->_kv.first << "应该是:" << (right - left) << endl;return false;}return abs(left - right) < 2 && _isBanlance(root->_left)&& _isBanlance(root->_right);}

AVL树删除

 AVL树作为了解型数据结构，只需掌握插入即可，如有兴趣，可以查看算法导论里AVL树的删除。

AVL树的性能 

 查找效率为logn，但是如果对AVL树进行结构修改，它会旋转很多次，因此如果需要高效查找并且不改变数据个数，可以考虑AVL树。