LeetCode 64. 最小路径和（动态规划）
创始人
2025-05-30 17:02:43

题目：

链接：LeetCode 64. 最小路径和
难度：中等
相关博文：剑指 Offer 47. 礼物的最大价值（动态规划）

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：
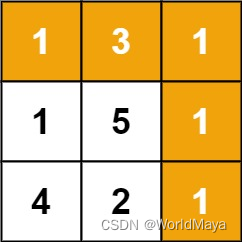
在这里插入图片描述

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 200
  • 0 <= grid[i][j] <= 100

动态规划：

dp[ i ][ j ] 状态定义：从左上角位置(0, 0)走到位置(i, j)的最小路径和。

状态转移方程：dp[ i ][ j ] = min(dp[ i - 1 ][ j ] + grid[ i ][ j ], dp[ i ][ j - 1] + grid[ i ][ j ])
在遍历过程中 dp[ i ][ j ] 有两种选择：要么从左边一格[ i ][ j - 1 ]移动过来，要么从上面一格[ i - 1 ][ j ]移动过来，选择两条路中数值和较小的那一条。

base case：dp[0][0] = grid[0][0]
左上角第一格是起始点，必选。

代码：

class Solution {
public:int minPathSum(vector>& grid) {int m = grid.size(), n = grid[0].size();vector> dp(m, vector(n));// base casedp[0][0] = grid[0][0];for(int i = 1; i < m; ++i) dp[i][0] = dp[i - 1][0] + grid[i][0]; // 第一列特殊处理for(int j = 1; j < n; ++j) dp[0][j] = dp[0][j - 1] + grid[0][j]; // 第一行特殊处理for(int i = 1; i < m; ++i)for(int j = 1; j < n; ++j)dp[i][j] = min(dp[i - 1][j] + grid[i][j], dp[i][j - 1] + grid[i][j]); //状态转移方程return dp[m - 1][n - 1];}
};

时间复杂度O(m * n），空间复杂度O(m* n)。

词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：安卓笔记-加油-奥利给！

下一篇：一名七年老安卓的一二月小结

相关内容

热门资讯

数据结构---队列 专栏：数据结构 个人主页：HaiFan. 专栏简介：这里是...
数字操作方法 系列文章目录 前端系列文章——传送门 JavaScript系列文章——传送门 文章目录系列文章目录...
Cartesi 2023 年 ... 查看 Cartesi Machine、Cartesi Rollups 和 Noether 的更新正在...
JavaWeb——jsp概述入... JSP定义:  在如下一个jsp文件里面有如下的代码  <%@ page content...
一切喜怒哀乐都来自于你的认知 01 有个学子，准备出国，父母请来清华的教授宁向东。请问教授࿱...
JAVA并发编程——synch... 引言         Java语言为了解决并发编程中存在的原子性、可见性和有序性问题，...
git学习----3.21 未... 文章目录前言Git ：一个分布式版本控制工具目标一、概述1.1 开发中的实际场景1.2...
Qt优秀开源项目之十七：QtP... QtPromise是Promises/A+规范的Qt/C++实现。该规范的译...
【前端八股文】JavaScri... 文章目录Set概念与arr的比较属性和方法并集、交集、差集Map概念属性和方法String用索引值和...
海康硬盘录像机接入RTSP/o... EasyNVR安防视频云服务平台可支持设备通过RTSP/Onvif协议接入平台，能提供...
在混合劳动力时代如何避免网络安... 在混合劳动力时代如何避免安全网络风险 三年多来，混合工作一直是工作生活中不可或缺的一...
2023还不懂Jmeter接口... 这里介绍的Jmeter接口测试的的实战，如果文章内容没遇看懂的话，我这边...
基于4G/5G弱网聚合的多链路... 基于4G/5G多卡聚合(弱网聚合)的智能融合通信设备技术亮点 增强带宽提供可靠连接 通过将多个有线和...
如何使用Synplify综合v... 文章目录使用Synplify综合的好处synplify的教程方法1（无效）...
2023年全国最新高校辅导员精... 百分百题库提供高校辅导员考试试题、辅导员考试预测题、高校辅导员考试真题、辅导员证考试题库等ÿ...
2022年18个值得期待的Le... 有数百个独特的LearnDash附加组件，您可能很难选择您的LearnDash LMS...
【java基础】Stream流... 文章目录基本介绍流的创建流的各种常见操作forEach方法filter方法map方法peek方法fl...
javaweb高校行政办公自动... 本课题基于我国高校管理信息化建设现状，结合在实际工作中所遇到的问题和收获，...
一款专门为自动化测试打造的集成... 你好，我是不二。 随着行业内卷越来越严重，自动化测试已成为测试工程师的...
【go-zero】golang... 一、casbin 概览 1、casbin基本了解 casbin的GitHub：https://git...
现在开发低代码平台算晚吗？ 现在开发低代码平台算晚吗？作为低代码的亲戚——零代码厂商，这篇就以“厂商...
【JavaWeb】书城项目（2... 222.书城项目-第三阶段：修改所有html页面为jsp页面 改成jsp页面之后&#x...
基于jeecgboot的大屏设...      通过前面设计好数据源后，就要进行数据集的设计了。      一、还是在onl...
Linux命令小技巧：显示文件... 工作中会有很多千奇百怪的需求，比如：如何在 Linux 命令行中快速找到...
【找工作】-- 大数据工程师找... 目录 1.前言 2.找工作的理论知识 2.1 分析个人特征 2.1.1 你自身优势是什么？
C++基础算法④——排序算法(... 排序算法 1.插入排序 2.桶排序 1.插入排序 基本思想：将初始数据分为有序部分和...
nginx快速入门.跟学B站n... nginx快速入门.跟学B站nginx一小时精讲课程笔记nginx简介及环境准备nginx简介环境准...
ORACLE存过互相调用之间事... 今天在问答区看到一个问题是 假如有procedureA、procedureB和procedureC&...
基于java中Springbo... 基于java中Springboot框影视影院订票选座管理系统 开发语言：Java 框...
CVE-2018-18086 最近闲来无事，看到青少年CTF平台，感觉对新手还是比较友好的࿰...