题解：

本题用到了记忆化搜索：记忆化搜索，本质还是 动态规划，只是实现方式采用了 深度优先搜索 的形式，但是它不像 深度优先搜索那样 重复 枚举所有情况，而是把已经计算的子问题保存下来，这样就和动态规划的思想不谋而合了。在本题中dp[i]表示得到第i种种子所需最短时间，如果纯深搜暴力，数据规模太大计算机承受不住！！！所以需要用dp[i]在一遍又一遍的递归中改变并保留数值，直到

if dp[i]!=math.inf:return dp[i]

下面具体探讨一下思路：

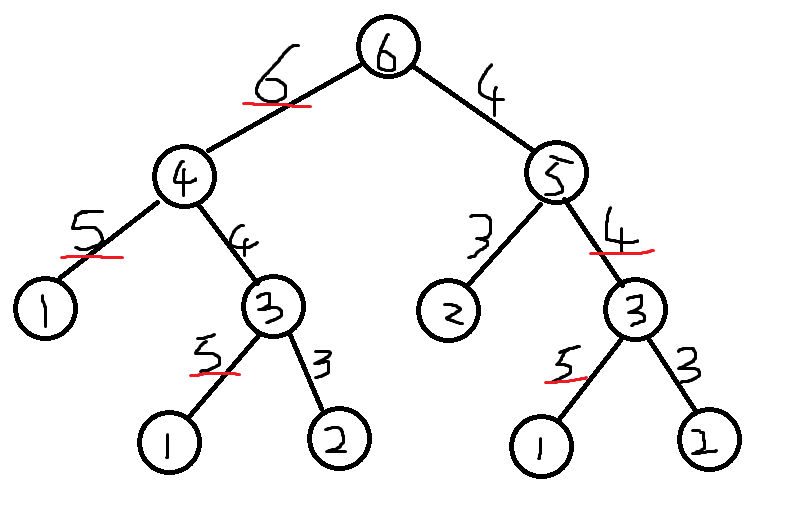
对于种子T来说：

1.两个子节点生长所需的时间取最大值

2.通过杂交得出两个子节点所需的时间取最大值

因为两个子节点可以同时杂交，所以只需要取两个子节点杂交所需时间的最大值，就是花费时间较长的子节点杂交完成后，则花费时间较短的子节点一定也杂交完成了，因为时间足够。所以只需要取两者的最大值。

这里我们采用列表的方式来记录杂交方式和对应的时间

from collections import defaultdict
#语法格式：
collections.defaultdict([default_factory[, …]])
该函数返回一个类似字典的对象。defaultdict是Python内建字典类（dict）的一个子类，
它重写了方法_missing_(key)，增加了一个可写的实例变量default_factory,
实例变量default_factory被missing()方法使用，如果该变量存在，则用以初始化构造器，
如果没有，则为None。其它的功能和dict一样。
nums=defaultdict(list)
nums[C].append([A,B,时间])
产生的格式是这样的：defaultdict(, {C: [[A,B,时间]]})
C代表着目标种子，A和B是杂交方案的输入量，时间即杂交时间

这里有非常重要的一点，我们需要把已有种子的dp值设为0，即dp[A]=0,dp[B]=0(假设A,B为已有的种子)

接下来是深搜五部曲：

1.参数：输入参数就是目标种子T，输出参数是dp[T]

2.结束递归条件：记忆化搜索结束递归条件应该就dp[i]着手展开，因为本题中dp[i]初始化都应是无穷大，所以结束递归条件应该是：

if dp[T]!=math.inf:return dp[T]

3.单层逻辑搜素：需要在单层逻辑搜索中不断更新保留dp[i]的值，目标种子直接对应两个子分支，所以直接for循环杂交字典：

for A,B,C in nums[T]:dp[T]=min(dp[T],max(time[A],time[B])+C)

4.输出打印：最后输出dp[T]即可

所以：

import os
import sys
# 请在此输入您的代码
N,M,K,T=map(int,input().split())
Ti=[0]+list(map(int,input().split()))
Kj=list(map(int,input().split()))
from collections import defaultdict
nums=defaultdict(list)
for i in range(K):A,B,C=map(int,input().split())nums[C].append([A,B,max(Ti[A],Ti[B])])
import math
dp=[math.inf]*(N+1)
for i in range(len(Kj)):dp[Kj[i]]=0
def DFS(T):if dp[T]!=math.inf:return dp[T]for A,B,C in nums[T]:dp[T]=min(dp[T],max(DFS(A),DFS(B))+C)return dp[T]
print(DFS(T))