Ripser.py学习 (1):概述
创始人
2025-05-31 05:28:24
文章目录
- 1 概述
- 2 安装
- 3 示意
1 概述
Ripser.py是一个用于持续同伦 (Persistent homology) 的Python库,其在C++ Ripser的基础上构建,提供了一些诸如以下的强大接口:
- 计算稀疏或者稠密数据的持续同伦。持续同伦是一种在拓扑数据分析中用来识别拓扑结构的方法。它可以用来分析一组数据的拓扑性质,通过检测数据的局部和全局的拓扑结构,可以提供对数据集的更深入的理解。在持续同伦的过程中,拓扑结构被表示为一系列的持久性特征,其中包括持续性间隙、持续性循环等。而拓扑结构的持续同伦则是指,在拓扑结构中不同维度的持续特征可以相互影响,并在一定程度上影响拓扑结构的演化。在拓扑数据分析中,持续同伦可以用来识别数据中的关键形状特征,例如孔洞、洞和环等;
- 可视化持久性图;
- 计算图像上的低星滤形 (Lowerstar filtration);
- 计算表征链(Representative cochain)。
参考地址:https://ripser.scikit-tda.org/en/latest/index.html
2 安装
Pipser库依赖于Cython库:
pip install cython
pip install ripser
3 示意
可以通过以下代码测试是否安装成功:
import numpy as np
from ripser import ripser
from persim import plot_diagramsdata = np.random.random((100, 2))
diagrams = ripser(data)['dgms']
plot_diagrams(diagrams, show=True)
输出如下:
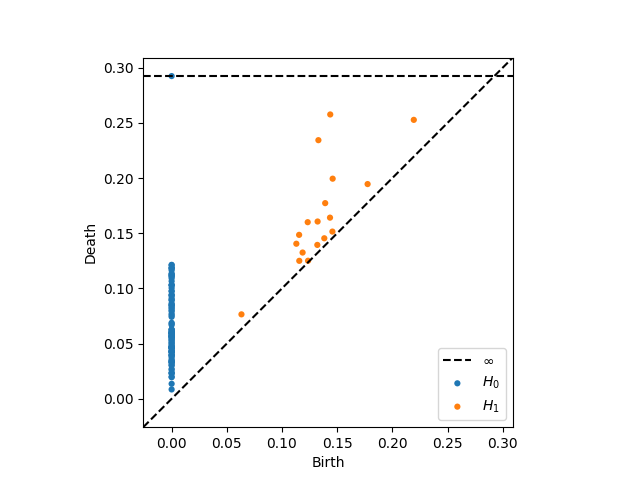
关于图中的H0H_0H0和H1H_1H1:
- H0H_0H0:表示一个拓扑空间中连通分支的数量。通常情况下它的值为1或更大的正整数,表示该空间有一个或多个连通分支;
- H1H_1H1:表示一个拓扑空间中的环的数量。如果一个空间是连通的但不是环的,那么H_1为零。如果有一条环,那么H1为零。如果有一条环,那么H_1为零。如果有一条环,那么H1就是整数1。如果有两个不相交的环,那么H_1$就是整数2,以此类推;
- H2H_2H2:表示一个拓扑空间中的空洞的数量。一个空洞可以被看作是一个二维的“空心环”,也就是一个环的内部又被一个环包围起来了。类似地,如果一个空间没有任何空洞,那么H2H_2H2为零。如果有一个空洞,那么H2为整数1。如果有两个不相交的空洞,那么H2H_2H2为整数2,以此类推。
以上代码还可以有以下替代方式:
import numpy as np
import matplotlib.pyplot as plt
from ripser import Ripsrips = Rips()
data = np.random.random((100,2))
diagrams = rips.fit_transform(data)
rips.plot(diagrams)
plt.show()
此时的绘制结果会有些许不同:
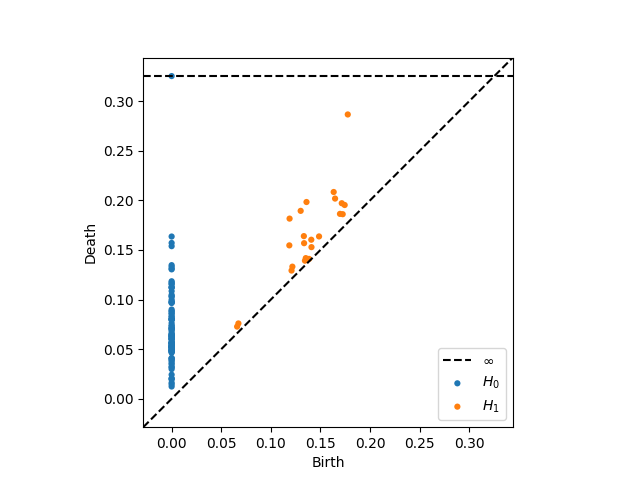
相关内容
热门资讯
世界上最漂亮的人 世界上最漂亮...
此前在某网上,选出了全球265万颜值姣好的女性。从这些数量庞大的女性群体中,人们投票选出了心目中最美...
北京的名胜古迹 北京最著名的景...
北京从元代开始,逐渐走上帝国首都的道路,先是成为大辽朝五大首都之一的南京城,随着金灭辽,金代从海陵王...
苗族的传统节日 贵州苗族节日有...
【岜沙苗族芦笙节】岜沙,苗语叫“分送”,距从江县城7.5公里,是世界上最崇拜树木并以树为神的枪手部落...
长白山自助游攻略 吉林长白山游...
昨天介绍了西坡的景点详细请看链接:一个人的旅行,据说能看到长白山天池全凭运气,您的运气如何?今日介绍...
应用未安装解决办法 平板应用未...
---IT小技术,每天Get一个小技能!一、前言描述苹果IPad2居然不能安装怎么办?与此IPad不...
