方向导数与梯度
1 方向导数(二元为例)
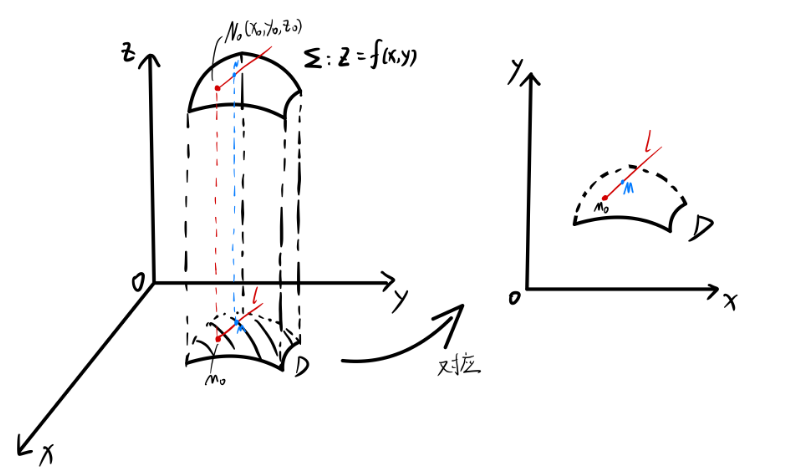
Σ:z=f(x,y),(x,y)∈D,M0(x0,y0)∈DΣ:z=f(x,y),(x,y)∈D,M_0(x_0,y_0)∈DΣ:z=f(x,y),(x,y)∈D,M0(x0,y0)∈D
在xoyxoyxoy面内从M0M_0M0作射线 lll ,取M(x0+△x,y+△y)∈lM(x_0+△x,y+△y)∈lM(x0+△x,y+△y)∈l
△z=f(x0+△x,y0+△y)−f(x0,y0)△z=f(x_0+△x,y_0+△y)-f(x_0,y_0)△z=f(x0+△x,y0+△y)−f(x0,y0)
ρ=∣M0M∣=(△x)2+(△y)2ρ=|M_0M|=\sqrt[]{(△x)^2+(△y)^2}ρ=∣M0M∣=(△x)2+(△y)2
如果 limρ→0△zρ\underset{ρ→0}{lim}\frac{△z}{ρ}ρ→0limρ△z存在,称此极限为z=f(x,y)z=f(x,y)z=f(x,y)在M0M_0M0处沿射线lll的方向导数,记作 ∂z∂l∣M0\frac{∂z}{∂l}|_{M_0}∂l∂z∣M0,
即∂z∂l∣M0≜limρ→0△zρ\frac{∂z}{∂l}|_{M_0}\triangleq\underset{ρ→0}{lim}\frac{△z}{ρ}∂l∂z∣M0≜ρ→0limρ△z
计算

z=f(x,y),M0(x0,y0)z=f(x,y),M_0(x_0,y_0)z=f(x,y),M0(x0,y0),射线 lll的方向余弦cosα,cosβcosα,cosβcosα,cosβ
f(x,y)f(x,y)f(x,y)连续可偏导
△zρ=f(x0+△x,y0+△y)−f(x0,y0+△y)ρ+f(x0,y0+△y)−f(x0,y0)ρ\frac{△z}{ρ}=\frac{f(x_0+△x,y_0+△y)-f(x_0,y_0+△y)}{ρ}+\frac{f(x_0,y_0+△y)-f(x_0,y_0)}{ρ}ρ△z=ρf(x0+△x,y0+△y)−f(x0,y0+△y)+ρf(x0,y0+△y)−f(x0,y0)
=fx(ξ,y0+△y)△xρ+f(x0,y0+△y)−f(x0,y0)△y⋅△yρf_x(ξ,y_0+△y)\frac{△x}{ρ}+\frac{f(x_0,y_0+△y)-f(x_0,y_0)}{△y}·\frac{△y}{ρ}fx(ξ,y0+△y)ρ△x+△yf(x0,y0+△y)−f(x0,y0)⋅ρ△y (ξ介于$$)
∵ fx(x,y),fy(x,y)f_x(x,y),f_y(x,y)fx(x,y),fy(x,y)连续
∴∂z∂l∣M0=limρ→0fx(ξ,y0+△y)△xρ+limρ→0f(x0,y0+△y)−f(x0,y0)△y⋅△yρ\frac{∂z}{∂l}|_{M_0}= \underset{ρ→0}{lim}f_x(ξ,y_0+△y)\frac{△x}{ρ}+\underset{ρ→0}{lim}\frac{f(x_0,y_0+△y)-f(x_0,y_0)}{△y}·\frac{△y}{ρ}∂l∂z∣M0=ρ→0limfx(ξ,y0+△y)ρ△x+ρ→0lim△yf(x0,y0+△y)−f(x0,y0)⋅ρ△y
=fx(x0,y0)cosα+fy(x0,y0)cosβf_x(x_0,y_0)cosα+f_y(x_0,y_0)cosβfx(x0,y0)cosα+fy(x0,y0)cosβ
即∂z∂l∣M0=∂z∂x∣M0cosα+∂z∂y∣M0cosβ\frac{∂z}{∂l}|_{M_0}=\frac{∂z}{∂x}|_{M_0}cosα+\frac{∂z}{∂y}|_{M_0}cosβ∂l∂z∣M0=∂x∂z∣M0cosα+∂y∂z∣M0cosβ
2 梯度(三元为例)
u=f(x,y,z)u=f(x,y,z)u=f(x,y,z)

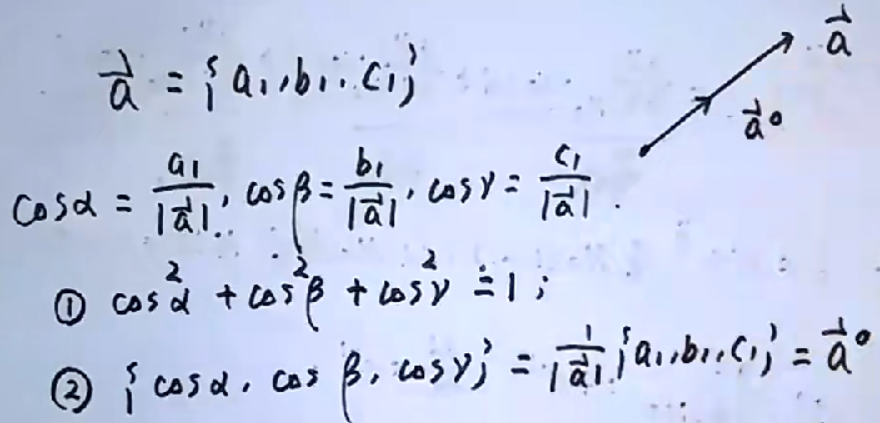
上一篇:【字符串】
下一篇:音视频技术开发周刊 | 285
