目录

• • 3.5、镜面反射项的重要性采样计算及简化近似（参考UE引擎实现中的思路）
  • • 3.5.1、法线分布函数的深度分析
    • 3.5.2、镜面反射项的蒙特卡洛积分形式
    • 3.5.3、利用 θh,ϕh\theta_h,\phi_hθh​,ϕh​ 与 θ,ϕ\theta,\phiθ,ϕ 之间的关系简化镜面积分项的蒙特卡洛积分形式

3.5、镜面反射项的重要性采样计算及简化近似（参考UE引擎实现中的思路）

  接着我们观察整个积分方程拆分后的第二项，也就是被称之为镜面反射项的部分：
Los(p⃗,ωo⃗)=∫Ω(DFG4(ωo⃗⋅n⃗)(ωi⃗⋅n⃗))Li(p⃗,ωi⃗)n⃗⋅ωi⃗dωi⃗D=NDFGGXTR(n⃗,h⃗,α)=α2π((n⃗⋅h⃗)2(α2−1)+1)2F=FSchlick(h⃗,ωo⃗,F0)=F0+(1−F0)(1−(h⃗⋅ωo⃗))5GSchlickGGX(n⃗,ωo⃗,κ)=n⃗⋅ωo⃗(n⃗⋅ωo⃗)(1−κ)+κκdirect=(α+1)28κIBL=α22G(n⃗,ωo⃗,ωi⃗,κ)=GSchlickGGX(n⃗,ωo⃗,κ)GSchlickGGX(n⃗,ωi⃗,κ)上列式子中：α=roughness2roughness∈[0.0,1.0]（粗糙度系数）h⃗=ωo⃗+ωi⃗∣ωo⃗+ωi⃗∣即出射方向与入射方向的中间向量\mathrm{L}_{o_s}(\vec{p},\vec{\omega_{o}}) = \mathop{\int}_{\Omega}(\frac{DFG}{4 ( \vec{\omega_o} \cdot \vec{n} ) (\vec{\omega_i} \cdot \vec{n} ) } ) \mathrm{L}_i(\vec{p},\vec{\omega_i}) \vec{n} \cdot \vec{\omega_i} d\vec{\omega_i} \\[2ex] D = NDF_{GGXTR}(\vec{n},\vec{h},\alpha) = \frac{ \alpha^2 }{\pi (( \vec{n} \cdot \vec{h} )^2(\alpha^2 - 1) + 1) ^ 2} \\[2ex] F = F_{Schlick}(\vec{h},\vec{\omega_o},F_0) = F_0 + ( 1 - F_0 )(1 - (\vec{h} \cdot \vec{\omega_o}))^5 \\[2ex] G_{SchlickGGX}(\vec{n},\vec{\omega_o},\kappa) = \frac{\vec{n} \cdot \vec{\omega_o}}{(\vec{n} \cdot \vec{\omega_o})(1-\kappa) + \kappa } \\[2ex] \kappa_{direct} = \frac{(\alpha + 1)^2}{8} \\[2ex] \kappa_{IBL} = \frac{\alpha^2}{2} \\[2ex] G(\vec{n},\vec{\omega_o},\vec{\omega_i},\kappa) = G_{SchlickGGX}(\vec{n},\vec{\omega_o},\kappa) G_{SchlickGGX}(\vec{n},\vec{\omega_i},\kappa) \\[2ex] 上列式子中：\alpha = roughness^2 \qquad roughness \in [ \ 0.0,1.0 \ ] （粗糙度系数） \\[2ex] \vec{h} = \cfrac{ \vec{\omega_o} + \vec{\omega_i} }{ \left| \vec{\omega_o} + \vec{\omega_i} \right| } \qquad 即出射方向与入射方向的中间向量 Los​​(p​,ωo​​)=∫Ω​(4(ωo​​⋅n)(ωi​​⋅n)DFG​)Li​(p​,ωi​​)n⋅ωi​​dωi​​D=NDFGGXTR​(n,h,α)=π((n⋅h)2(α2−1)+1)2α2​F=FSchlick​(h,ωo​​,F0​)=F0​+(1−F0​)(1−(h⋅ωo​​))5GSchlickGGX​(n,ωo​​,κ)=(n⋅ωo​​)(1−κ)+κn⋅ωo​​​κdirect​=8(α+1)2​κIBL​=2α2​G(n,ωo​​,ωi​​,κ)=GSchlickGGX​(n,ωo​​,κ)GSchlickGGX​(n,ωi​​,κ)上列式子中：α=roughness2roughness∈[ 0.0,1.0 ]（粗糙度系数）h=∣ωo​​+ωi​​∣ωo​​+ωi​​​即出射方向与入射方向的中间向量

3.5.1、法线分布函数的深度分析

  从上式中被积分项的每一个函数可以看出来，这个被积分项是异常复杂的。如果刚才关于漫反射辐照度预积分的计算过程看明白了的话，到这里我们首先应该想到，这个积分也一定能够使用重要性采样方法进行高效的计算，只是推导的可能有点复杂。

  一般情况下，针对这样的复杂积分的情况，首先就是要分析其函数、自变量的情况，然后看看是否有能够简化的余地。

  而对于镜面反射项来说，重要的函数就是 DFG 这 3 个函数，而通过观察我们可以发现其中被称为“法线分布函数”的 DGGXD_{GGX}DGGX​ 的函数的自变量是最简单的，它中间只有一个自由变量 h⃗\vec{h}h ，也就是入射光和出射光的中间向量，并且是跟积分立体角微元相关联的，而其他的参数，如粗糙度系数 roughness，则只跟被照射点 p⃗\vec{p}p​ 相关联，因此在每一帧渲染时，这些其它的参数对于镜面反射项来说基本就等同于是常数了。

  另外从微平面理论角度出发，法线分布函数 DGGXD_{GGX}DGGX​ 的含义是说，假设一点处的反射面在更微观的尺度上由很多更小的随机朝向微表面元构成， DGGXD_{GGX}DGGX​ 就表达了这些更小的微表面元上的法线朝向的概率密度函数（PDF），所以它就跟粗糙度紧密相关，因为越粗糙的表面上我们认为其微表面朝向就更随机。之所以使用法线的概率分布来表达这一概念，主要是因为在整个 PBR 模型中，我们一直探讨的都是从微分角度出发，分析一个点处的光线反射问题，而光线反射问题中关注的就主要是该点处的法线方向。

  既然 DGGXD_{GGX}DGGX​ 是概率密度函数，那么根据之前学习的蒙特卡洛积分的方法，就可以考虑将这个函数作为我们将要选择的概率密度函数的一部分，这样最终再进行蒙特卡洛积分计算时就应该可以将这个因子从分子分母中同时约掉，从而减少一个函数的计算。这也是使用蒙特卡洛重要性采样方法时的一个重要的技巧。

  为了做到这一点，我们先来对镜面反射积分项做下整理。主要先将几个矢量表达式、立体角微元变换为三角函数的形式，方便处理：
∵dω=sin⁡(θ)dθdϕ,n⃗⋅ωi⃗=cos⁡(θ)∴Los(p⃗,ωo⃗)=∫Ω(DFG4(ωo⃗⋅n⃗)(ωi⃗⋅n⃗))Li(p⃗,ωi⃗)n⃗⋅ωi⃗dωi⃗=∫Ω(DFG4(ωo⃗⋅n⃗)(ωi⃗⋅n⃗))Li(p⃗,ωi⃗)cos⁡(θ)sin⁡(θ)dθdϕ\because \quad \mathrm{d} \omega = \sin(\theta) \mathrm{d} \theta \mathrm{d}\phi, \quad \vec{n} \cdot \vec{\omega_i} = \cos(\theta) \\[2ex] \therefore \quad \mathrm{L}_{o_s}(\vec{p},\vec{\omega_{o}}) = \mathop{\int}_{\Omega}(\frac{DFG}{4 ( \vec{\omega_o} \cdot \vec{n} ) (\vec{\omega_i} \cdot \vec{n} ) } ) \mathrm{L}_i(\vec{p},\vec{\omega_i}) \vec{n} \cdot \vec{\omega_i} \mathrm{d} \vec{\omega_i} \\[2ex] = \mathop{\int}_{\Omega}(\frac{DFG}{4 ( \vec{\omega_o} \cdot \vec{n} ) (\vec{\omega_i} \cdot \vec{n} ) } ) \mathrm{L}_i(\vec{p},\vec{\omega_i}) \cos(\theta)\sin(\theta) \mathrm{d}\theta \mathrm{d} \phi ∵dω=sin(θ)dθdϕ,n⋅ωi​​=cos(θ)∴Los​​(p​,ωo​​)=∫Ω​(4(ωo​​⋅n)(ωi​​⋅n)DFG​)Li​(p​,ωi​​)n⋅ωi​​dωi​​=∫Ω​(4(ωo​​⋅n)(ωi​​⋅n)DFG​)Li​(p​,ωi​​)cos(θ)sin(θ)dθdϕ
  此时使用与之前处理漫反射项时一样的瞪眼法，可以假设这时我们需要的概率密度函数为：
p(θ,ϕ)=DGGX(h⃗)cos⁡(θh)sin⁡(θh)\mathrm{p}(\theta,\phi) = D_{GGX}(\vec{h}) \cos(\theta_h) \sin(\theta_h) p(θ,ϕ)=DGGX​(h)cos(θh​)sin(θh​)
  之所以选择函数 DGGXD_{GGX}DGGX​ ，主要是因为它表达的就是微表面下的法线分布的情况，如果它的值大则说明函数被采样的概率就高，也就是微表面的法线方向与表面的法线方向比较靠近，因此反射贡献也就较大，所以最终这个函数其实影响了 BFDF 函数值的大小，从而影响了反射光的大小，因此选择它作为重要性采样的概率密度函数的一部分是非常合适的。

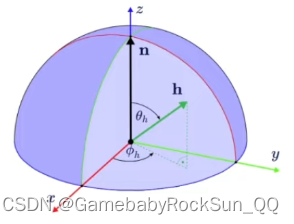
  这里还需要注意个细节就是，因为函数 DGGXD_{GGX}DGGX​ 的主要参数是 h⃗\vec{h}h ，所以在取概率密度函数时，其三角函数部分也取针对 h⃗\vec{h}h 的变量 θh,ϕh\theta_h,\phi_hθh​,ϕh​ ，其含义如下图所示：

  此时，因为 DGGXD_{GGX}DGGX​ 函数表达式已知，那我们就验证一下它是否满足“归一条件”：
∫Ωp(θh,ϕh)dωh=∫02π∫0π2DGGX(h⃗)cos⁡(θh)sin⁡(θh)dθhdϕh=∫02π∫0π2α2cos⁡(θh)sin⁡(θh)π((α2−1)cos⁡2(θh)+1)2dθhdϕh∵dcos⁡2(t)=−2cos⁡(t)sin⁡(t)dt=2π[α2π(2α2−2)((α2−1)cos⁡2(θh)+1)]0π2=1α2−1(α2(α2−1)cos⁡2(π2)+1−α2(α2−1)cos⁡2(0)+1)=1(α2−1)×(α2−1)=1即：∫Ωp(θh,ϕh)dωh=1\int \limits_{\Omega} \mathrm{p}(\theta_h,\phi_h) \mathrm{d} \omega_h \\[2ex] = \int\limits_0^{2\pi} \int \limits_0^{\frac{\pi}{2}} D_{GGX}(\vec{h}) \cos(\theta_h)\sin(\theta_h) \mathrm{d}\theta_h \mathrm{d}\phi_h \\[2ex] = \int \limits_0^{2\pi} \int \limits_0^{\frac{\pi}{2}} \cfrac{\alpha^2\cos(\theta_h) \sin(\theta_h)}{\pi((\alpha^2-1)\cos^2(\theta_h)+1)^2} \mathrm{d}\theta_h \mathrm{d}\phi_h \\[2ex] \because \quad \mathrm{d}\cos^2(t) = -2\cos(t)\sin(t)\mathrm{d}t \\[2ex] =2\pi\left[ \cfrac{\alpha^2}{\pi(2\alpha^2-2)((\alpha^2-1)\cos^2(\theta_h)+1)} \right]_0^{\frac{\pi}{2}} \\[2ex] = \cfrac{1}{\alpha^2-1} \left( \cfrac{\alpha^2}{(\alpha^2-1)\cos^2(\frac{\pi}{2})+1} - \cfrac{\alpha^2}{ ( \alpha^2 - 1 ) \cos^2(0) + 1} \right) \\[2ex] = \cfrac{1}{(\alpha^2-1)} \times (\alpha^2 - 1 ) \\[2ex] =1 \\[2ex] 即： \int \limits_{\Omega} \mathrm{p}(\theta_h,\phi_h) \mathrm{d}\omega_h = 1 Ω∫​p(θh​,ϕh​)dωh​=0∫2π​0∫2π​​DGGX​(h)cos(θh​)sin(θh​)dθh​dϕh​=0∫2π​0∫2π​​π((α2−1)cos2(θh​)+1)2α2cos(θh​)sin(θh​)​dθh​dϕh​∵dcos2(t)=−2cos(t)sin(t)dt=2π[π(2α2−2)((α2−1)cos2(θh​)+1)α2​]02π​​=α2−11​((α2−1)cos2(2π​)+1α2​−(α2−1)cos2(0)+1α2​)=(α2−1)1​×(α2−1)=1即：Ω∫​p(θh​,ϕh​)dωh​=1
  这个结果很棒，说明我们选择的关于 θh,ϕh\theta_h,\phi_hθh​,ϕh​ 的概率密度函数天生就是 “归一化”的。当然这不是一个巧合，因为 DGGXD_{GGX}DGGX​ 函数本就是被 “设计” 出来的函数，所以它肯定需要满足这些要求。

3.5.2、镜面反射项的蒙特卡洛积分形式

  既然已经找到了镜面反射项被积变量的概率密度函数，那么接着就是按照蒙特卡洛积分的步骤，继续计算其分布函数 CDF，当然因为是二元概率密度函数，那么首先需要分析出针对每个变量的边缘概率密度函数：
p(ϕh)=∫0π2p(θh,ϕh)dθh=∫0π2α2cos⁡(θh)sin⁡(θh)π((α2−1)cos⁡2(θh)+1)2dθh∵dcos⁡2(t)=−2cos⁡(t)sin⁡(t)dt=[α2π(2α2−2)((α2−1)cos⁡2(θh)+1)]0π2=12π[α2(α2−1)((α2−1)cos⁡2(θh)+1)]0π2=12π∵p(θh,ϕh)=p(θh)p(ϕh)=p(θh)12π∴p(θh)=2πp(θh,ϕh)=2πα2π(cos⁡2(θh)(α2−1)+1)2cos⁡(θh)sin⁡(θh)=2α2(cos⁡2(θh)(α2−1)+1)2cos⁡(θh)sin⁡(θh)\mathrm{p}(\phi_h) = \int \limits_{0}^{\frac{\pi}{2}} \mathrm{p}(\theta_h,\phi_h) \mathrm{d} \theta_h \\[2ex] = \int \limits_0^{\frac{\pi}{2}} \cfrac{\alpha^2\cos(\theta_h) \sin(\theta_h)}{\pi((\alpha^2-1)\cos^2(\theta_h)+1)^2} \mathrm{d}\theta_h \\[2ex] \because \quad \mathrm{d}\cos^2(t) = -2\cos(t)\sin(t)\mathrm{d}t \\[2ex] =\left[ \cfrac{\alpha^2}{\pi(2\alpha^2-2)((\alpha^2-1)\cos^2(\theta_h)+1)} \right]_0^{\frac{\pi}{2}} \\[2ex] = \cfrac{1}{2\pi} \left[ \cfrac{\alpha^2}{(\alpha^2-1)((\alpha^2-1)\cos^2(\theta_h)+1)} \right]_0^{\frac{\pi}{2}} \\[2ex] = \cfrac{1}{2\pi} \\[2ex] \because \quad \mathrm{p}(\theta_h,\phi_h) = \mathrm{p}(\theta_h)\mathrm{p}(\phi_h) = \mathrm{p}(\theta_h) \cfrac{1}{2\pi} \\[2ex] \therefore \quad \mathrm{p}(\theta_h) = 2\pi \mathrm{p}(\theta_h,\phi_h) \\[2ex] = 2 \pi \cfrac{\alpha^2}{\pi(\cos^2(\theta_h)(\alpha^2-1)+1)^2} \cos(\theta_h) \sin(\theta_h) \\[2ex] = \cfrac{2\alpha^2}{(\cos^2(\theta_h)(\alpha^2-1)+1)^2} \cos(\theta_h) \sin(\theta_h) p(ϕh​)=0∫2π​​p(θh​,ϕh​)dθh​=0∫2π​​π((α2−1)cos2(θh​)+1)2α2cos(θh​)sin(θh​)​dθh​∵dcos2(t)=−2cos(t)sin(t)dt=[π(2α2−2)((α2−1)cos2(θh​)+1)α2​]02π​​=2π1​[(α2−1)((α2−1)cos2(θh​)+1)α2​]02π​​=2π1​∵p(θh​,ϕh​)=p(θh​)p(ϕh​)=p(θh​)2π1​∴p(θh​)=2πp(θh​,ϕh​)=2ππ(cos2(θh​)(α2−1)+1)2α2​cos(θh​)sin(θh​)=(cos2(θh​)(α2−1)+1)22α2​cos(θh​)sin(θh​)
  至此，虽然表达式看上去有些复杂，但一切还是在我们的掌控之中，接着让我们继续计算两个变量各自的 CDF 及其反函数：
CDF(θh)=∫0θhp(θ~h)dθ~h=∫0θh2α2(cos⁡2(θ~h)(α2−1)+1)2cos⁡(θ~h)sin⁡(θ~h)dθ~h∵dcos⁡2(t)=−2cos⁡(t)sin⁡(t)dt∴=∫0θh−α2×dcos⁡2(θ~h)(cos⁡2(θ~h)(α2−1)+1)2∀cos⁡2(θ~h)=t=∫0arccos⁡(t)−α2dt((α2−1)×t+1)2=[α2α2−1×1(α2−1)t+1]0arccos⁡(t)=[α2(α2−1)(cos⁡2(θ~)(α2−1)+1))]0θh=α2(α2−1)(cos⁡2(θh)(α2−1)+1)−α2(α2−1)(cos⁡2(0)(α2−1)+1)=α2(α2−1)(cos⁡2(θh)(α2−1)+1)−1(α2−1)\mathrm{CDF}(\theta_h) = \int \limits_0^{\theta_h} \mathrm{p}(\tilde{\theta}_h) \mathrm{d} \tilde{\theta}_h \\[2ex] = \int \limits_0^{\theta_h} \cfrac{2\alpha^2}{(\cos^2(\tilde{\theta}_h)(\alpha^2-1)+1)^2} \cos(\tilde{\theta}_h) \sin(\tilde{\theta}_h) \mathrm{d} \tilde{\theta}_h \\[2ex] \because \quad \mathrm{d}\cos^2(t) = -2\cos(t)\sin(t)\mathrm{d}t \\[2ex] \therefore \\[2ex] = \int \limits_0^{\theta_h} \cfrac{-\alpha^2 \times \mathrm{d} \cos^2(\tilde{\theta}_h) }{(\cos^2(\tilde{\theta}_h)(\alpha^2-1)+1)^2} \\[2ex] \forall \quad \cos^2(\tilde{\theta}_h) = t \\[2ex] =\int \limits_0^{\arccos(\sqrt{t})} \cfrac{-\alpha^2 \mathrm{d} t }{((\alpha^2-1) \times t+1)^2} \\[2ex] =\left[ \cfrac{\alpha^2}{\alpha^2-1} \times \cfrac{1}{(\alpha^2-1)t +1} \right]_0^{\arccos(\sqrt{t})} \\[2ex] =\left[ \cfrac{\alpha^2}{(\alpha^2-1)\left(\cos^2(\tilde{\theta})(\alpha^2-1)+1) \right)} \right]_0^{\theta_h} \\[2ex] = \cfrac{\alpha^2}{(\alpha^2-1)(\cos^2(\theta_h)(\alpha^2-1)+1)}-\cfrac{\alpha^2}{(\alpha^2-1)(\cos^2(0)(\alpha^2-1)+1)} \\[2ex] = \cfrac{\alpha^2}{(\alpha^2-1)(\cos^2(\theta_h)(\alpha^2-1)+1)}-\cfrac{1}{(\alpha^2-1)} CDF(θh​)=0∫θh​​p(θ~h​)dθ~h​=0∫θh​​(cos2(θ~h​)(α2−1)+1)22α2​cos(θ~h​)sin(θ~h​)dθ~h​∵dcos2(t)=−2cos(t)sin(t)dt∴=0∫θh​​(cos2(θ~h​)(α2−1)+1)2−α2×dcos2(θ~h​)​∀cos2(θ~h​)=t=0∫arccos(t​)​((α2−1)×t+1)2−α2dt​=[α2−1α2​×(α2−1)t+11​]0arccos(t​)​=​(α2−1)(cos2(θ~)(α2−1)+1))α2​​0θh​​=(α2−1)(cos2(θh​)(α2−1)+1)α2​−(α2−1)(cos2(0)(α2−1)+1)α2​=(α2−1)(cos2(θh​)(α2−1)+1)α2​−(α2−1)1​
  因为 DGGXD_{GGX}DGGX​ 函数的繁琐，所以上式推导过程中，尽力为大家展示清楚了整个积分换元方法的过程，也算为之前的几个积分计算过程做一个有力补充，尤其是为数学功底不强的同学。这里要特别注意积分变量和积分上限变量的区别。同样的方法我们可以计算出 CDF(ϕh)CDF(\phi_h)CDF(ϕh​)如下：
CDF(ϕh)=∫0ϕh12πdϕ~=12πϕh\mathrm{CDF}(\phi_h) = \int \limits_0^{\phi_h} \cfrac{1}{2\pi} \mathrm{d} \tilde{\phi} \\[2ex] = \cfrac{1}{2\pi} \phi_h CDF(ϕh​)=0∫ϕh​​2π1​dϕ~​=2π1​ϕh​
  有了CDF，我们就接着来推导他们的反函数：
μ=CDF(θh)=α2(α2−1)(cos⁡2(θh)(α2−1)+1)−1(α2−1)⇒μ+1(α2−1)=α2(α2−1)(cos⁡2(θh)(α2−1)+1)μ(α2−1)α2+1α2=1(cos⁡2(θh)(α2−1)+1)μ(α2−1)+1α2=1(cos⁡2(θh)(α2−1)+1)α2μ(α2−1)+1=(cos⁡2(θh)(α2−1)+1)α2μ(α2−1)+1−1=cos⁡2(θh)(α2−1)α2μ(α2−1)+1−1=cos⁡2(θh)(α2−1)α2(α2−1)(μ(α2−1)+1)−1(α2−1)=cos⁡2(θh)cos⁡2(θh)=α2−(μ(α2−1)+1)(α2−1)(μ(α2−1)+1)cos⁡2(θh)=(α2−1)−μ(α2−1)(α2−1)(μ(α2−1)+1)cos⁡2(θh)=1−μμ(α2−1)+1cos⁡(θh)=1−μμ(α2−1)+1θh=arccos⁡1−μμ(α2−1)+1=CDFθh−1(μ)\mu = \mathrm{CDF}(\theta_h) \\[2ex] = \cfrac{\alpha^2}{(\alpha^2-1)(\cos^2(\theta_h)(\alpha^2-1)+1)}-\cfrac{1}{(\alpha^2-1)} \\[2ex] \Rightarrow \mu + \cfrac{1}{(\alpha^2-1)} = \cfrac{\alpha^2}{(\alpha^2-1)(\cos^2(\theta_h)(\alpha^2-1)+1)} \\[2ex] \cfrac{\mu(\alpha^2-1)}{\alpha^2} + \cfrac{1}{\alpha^2} = \cfrac{1}{(\cos^2(\theta_h)(\alpha^2-1)+1)} \\[2ex] \cfrac{\mu(\alpha^2-1) + 1}{\alpha^2} = \cfrac{1}{(\cos^2(\theta_h)(\alpha^2-1)+1)} \\[2ex] \cfrac{\alpha^2}{\mu(\alpha^2-1) + 1} = (\cos^2(\theta_h)(\alpha^2-1)+1) \\[2ex] \cfrac{\alpha^2}{\mu(\alpha^2-1) + 1} - 1 = \cos^2(\theta_h)(\alpha^2-1) \\[2ex] \cfrac{\alpha^2}{\mu(\alpha^2-1) + 1} - 1 = \cos^2(\theta_h)(\alpha^2-1) \\[2ex] \cfrac{\alpha^2}{(\alpha^2-1)(\mu(\alpha^2-1) + 1)} - \cfrac{1}{(\alpha^2-1)} = \cos^2(\theta_h) \\[2ex] \cos^2(\theta_h) = \cfrac{\alpha^2 - (\mu(\alpha^2-1) + 1)}{(\alpha^2-1)(\mu(\alpha^2-1) + 1)} \\[2ex] \cos^2(\theta_h) = \cfrac{(\alpha^2 - 1) - \mu(\alpha^2-1) }{(\alpha^2-1)(\mu(\alpha^2-1) + 1)} \\[2ex] \cos^2(\theta_h) = \cfrac{1 - \mu }{\mu(\alpha^2-1) + 1} \\[2ex] \cos(\theta_h) = \sqrt{\cfrac{1 - \mu }{\mu(\alpha^2-1) + 1}} \\[2ex] \theta_h = \arccos{\sqrt{\cfrac{1 - \mu }{\mu(\alpha^2-1) + 1}}} \\[2ex] = \mathrm{CDF}_{\theta_h}^{-1}(\mu) μ=CDF(θh​)=(α2−1)(cos2(θh​)(α2−1)+1)α2​−(α2−1)1​⇒μ+(α2−1)1​=(α2−1)(cos2(θh​)(α2−1)+1)α2​α2μ(α2−1)​+α21​=(cos2(θh​)(α2−1)+1)1​α2μ(α2−1)+1​=(cos2(θh​)(α2−1)+1)1​μ(α2−1)+1α2​=(cos2(θh​)(α2−1)+1)μ(α2−1)+1α2​−1=cos2(θh​)(α2−1)μ(α2−1)+1α2​−1=cos2(θh​)(α2−1)(α2−1)(μ(α2−1)+1)α2​−(α2−1)1​=cos2(θh​)cos2(θh​)=(α2−1)(μ(α2−1)+1)α2−(μ(α2−1)+1)​cos2(θh​)=(α2−1)(μ(α2−1)+1)(α2−1)−μ(α2−1)​cos2(θh​)=μ(α2−1)+11−μ​cos(θh​)=μ(α2−1)+11−μ​​θh​=arccosμ(α2−1)+11−μ​​=CDFθh​−1​(μ)
  上面的过程虽然复杂，但其实基本都是中学数学的内容而已，展示在这里主要是为了让大家明白，最终我们需要怎么生成自变量θh\theta_hθh​ 对应的偏差最小的随机序列。同样的我们有：
ν=12πϕh⇒ϕh=2πν=CDFϕh−1(ν)\nu = \cfrac{1}{2\pi} \phi_h \\[2ex] \Rightarrow \quad \phi_h = 2 \pi \nu = CDF_{\phi_h}^{-1}(\nu) ν=2π1​ϕh​⇒ϕh​=2πν=CDFϕh​−1​(ν)
  在本章示例代码中，就使用了上面两个 CDF 反函数的结果，并使用均匀分布的伪随机序列生成函数，以及球坐标到笛卡尔坐标转换的公式，最终生成了重要性采样需要的随机向量 h⃗\vec{h}h，这也是 UE 引擎中代码中使用的方法。 在本章示例代码中，具体实现如下：

float3 ImportanceSampleGGX(float2 Xi, float3 N, float roughness)
{float a = roughness * roughness;float phi = 2.0f * PI * Xi.x;float cosTheta = sqrt((1.0f - Xi.y) / (1.0f + (a * a - 1.0f) * Xi.y));float sinTheta = sqrt(1.0f - cosTheta * cosTheta);float3 H;H.x = cos(phi) * sinTheta;H.y = sin(phi) * sinTheta;H.z = cosTheta;float3 up = abs(N.z) < 0.999 ? float3(0.0f, 0.0f, 1.0f) : float3(1.0f, 0.0f, 0.0f);float3 tangent = normalize(cross(up, N));float3 bitangent = cross(N, tangent);float3 sampleVec = tangent * H.x + bitangent * H.y + N * H.z;return normalize(sampleVec);
}

  代码中 Xi 变量中就按 2D 向量形式分别存储两个均匀分布的范围在 [0,1][0,1][0,1] 之间的伪随机数。同时代码使用了我们在介绍漫反射辐照度贴图生成随机变量时介绍的方法，即不再求反三角函数了，而是直接当其为三角函数值，简化计算。

  如果之前的重要性采样的数学推导过程完全搞懂了的话，那么这段代码就没啥不好理解的，同样你也就可以完全无障碍的看懂 UE 中的实现了：

float4 ImportanceSampleGGX( float2 E, float a2 )
{float Phi = 2 * PI * E.x;float CosTheta = sqrt( (1 - E.y) / ( 1 + (a2 - 1) * E.y ) );float SinTheta = sqrt( 1 - CosTheta * CosTheta );float3 H;H.x = SinTheta * cos( Phi );H.y = SinTheta * sin( Phi );H.z = CosTheta;float d = ( CosTheta * a2 - CosTheta ) * CosTheta + 1;float D = a2 / ( PI*d*d );float PDF = D * CosTheta;return float4( H, PDF );
}

3.5.3、利用 θh,ϕh\theta_h,\phi_hθh​,ϕh​ 与 θ,ϕ\theta,\phiθ,ϕ 之间的关系简化镜面积分项的蒙特卡洛积分形式

  按照蒙特卡洛积分重要性采样的步骤，现在我们还需要将镜面反射项积分整体转换为蒙特卡洛积分的形式。根据前面的推导我们有：
Los(p⃗,ωo⃗)=∫Ω(DFG4(ωo⃗⋅n⃗)(ωi⃗⋅n⃗))Li(p⃗,ωi⃗)cos⁡(θ)sin⁡(θ)dθdϕ\mathrm{L}_{o_s}(\vec{p},\vec{\omega_{o}}) = \mathop{\int}_{\Omega}(\frac{DFG}{4 ( \vec{\omega_o} \cdot \vec{n} ) (\vec{\omega_i} \cdot \vec{n} ) } ) \mathrm{L}_i(\vec{p},\vec{\omega_i}) \cos(\theta)\sin(\theta) \mathrm{d}\theta \mathrm{d} \phi Los​​(p​,ωo​​)=∫Ω​(4(ωo​​⋅n)(ωi​​⋅n)DFG​)Li​(p​,ωi​​)cos(θ)sin(θ)dθdϕ
  此时我们发现，之前用瞪眼法生成的概率密度函数 p(θh,ϕh)p(\theta_h,\phi_h)p(θh​,ϕh​) 是关于变量 θh,ϕh\theta_h,\phi_hθh​,ϕh​ 的，而不是关于 θ,ϕ\theta,\phiθ,ϕ 的。此时就需要对积分微元做进一步的变换，或者称之为换元。这就需要我们退回立体角微分形式先：
Los(p⃗,ωo⃗)=∫Ω(DFG4(ωo⃗⋅n⃗)(ωi⃗⋅n⃗))Li(p⃗)cos⁡(θ)dωi⃗=∫Ωh(DFG4(ωo⃗⋅n⃗)(ωi⃗⋅n⃗))Li(p⃗)cos⁡(θ)dωi⃗dωh⃗dωh⃗∵dωi=sin⁡(θ)dϕ⋅dθdωh=sin⁡(θh)dϕh⋅dθh∴=∫Ωh(DFG4(ωo⃗⋅n⃗)(ωi⃗⋅n⃗))Li(p⃗)cos⁡(θ)sin⁡(θ)dϕ⋅dθsin⁡(θh)dϕh⋅dθhdωh\mathrm{L}_{o_s}(\vec{p},\vec{\omega_{o}}) = \mathop{\int}_{\Omega}(\frac{DFG}{4 ( \vec{\omega_o} \cdot \vec{n} ) (\vec{\omega_i} \cdot \vec{n} ) } ) \mathrm{L}_i(\vec{p}) \cos(\theta) \mathrm{d} \vec{\omega_i} \\[2ex] = \mathop{\int}_{\Omega_h}(\frac{DFG}{4 ( \vec{\omega_o} \cdot \vec{n} ) (\vec{\omega_i} \cdot \vec{n} ) } ) \mathrm{L}_i(\vec{p}) \cos(\theta) \cfrac{\mathrm{d} \vec{\omega_i}}{\mathrm{d} \vec{\omega_h}} \mathrm{d} \vec{\omega_h} \\[2ex] \because \quad \mathrm{d}\omega_i = \sin(\theta)\mathrm{d}\phi \cdot \mathrm{d}\theta \quad \mathrm{d}\omega_h = \sin(\theta_h)\mathrm{d}\phi_h \cdot \mathrm{d}\theta_h \\[2ex] \therefore = \mathop{\int}_{\Omega_h}(\frac{DFG}{4 ( \vec{\omega_o} \cdot \vec{n} ) (\vec{\omega_i} \cdot \vec{n} ) } ) \mathrm{L}_i(\vec{p}) \cos(\theta) \cfrac{\sin(\theta)\mathrm{d}\phi \cdot \mathrm{d}\theta}{\sin(\theta_h)\mathrm{d}\phi_h \cdot \mathrm{d}\theta_h} \mathrm{d} \omega_h Los​​(p​,ωo​​)=∫Ω​(4(ωo​​⋅n)(ωi​​⋅n)DFG​)Li​(p​)cos(θ)dωi​​=∫Ωh​​(4(ωo​​⋅n)(ωi​​⋅n)DFG​)Li​(p​)cos(θ)dωh​​dωi​​​dωh​​∵dωi​=sin(θ)dϕ⋅dθdωh​=sin(θh​)dϕh​⋅dθh​∴=∫Ωh​​(4(ωo​​⋅n)(ωi​​⋅n)DFG​)Li​(p​)cos(θ)sin(θh​)dϕh​⋅dθh​sin(θ)dϕ⋅dθ​dωh​
  推导到这里时，有个特殊的关系，就是说因为式中 sin⁡(θ)dϕdθ\sin(\theta)\mathrm{d}\phi \mathrm{d}\thetasin(θ)dϕdθ 其实是针对点 p⃗\vec{p}p​ 处表面法线 n⃗\vec{n}n 来说的角度值，其关系如下图所示：

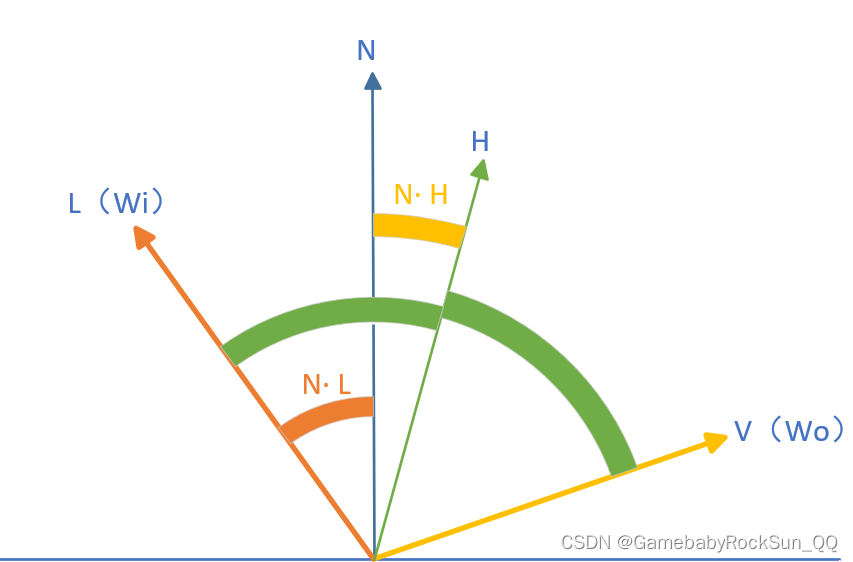
  注意图中关系 N⋅L=n⃗⋅ωi⃗=cos⁡(θ),N⋅H=n⃗⋅h⃗=cos⁡(θh)N \cdot L = \vec{n} \cdot \vec{\omega_i} = \cos(\theta), \quad N \cdot H = \vec{n} \cdot \vec{h} = \cos(\theta_h)N⋅L=n⋅ωi​​=cos(θ),N⋅H=n⋅h=cos(θh​) ，此时无法简单的表达 θ与θh\theta 与 \theta_hθ与θh​ 之间的关系。

  因为实际情况下，h⃗\vec{h}h 是入射方向 ω⃗i\vec{\omega}_iωi​ 和视见方向 ω⃗o\vec{\omega}_oωo​ 的中间向量，也即 h⃗=ωo⃗+ωi⃗∣ωo⃗+ωi⃗∣\vec{h} = \cfrac{ \vec{\omega_o} + \vec{\omega_i} }{ \left| \vec{\omega_o} + \vec{\omega_i} \right| }h=∣ωo​​+ωi​​∣ωo​​+ωi​​​ 。这时因为 ω⃗o\vec{\omega}_oωo​ 在每一帧会因摄像机位置的变动而不同。所以这最终导致我们无法简单的知道 θ与θh\theta 与 \theta_hθ与θh​ 之间的简单关系，同时最严重的是，这还将导致整个积分计算过程必须要放到渲染循环中实时计算，这样就会导致计算量过大，使的整个实时 PBR 都无法实现，也即没法在一秒钟内显示至少25帧以上画面，也就失去了意义。

  此时在实时 PBR 实际处理中，就假定视方向就是点 p⃗\vec{p}p​ 处的法线方向（更严格的说法是假定法线方向永远是 Z 轴，而视见方向始终在 XoZ 平面内，并且最终视见方向与法线方向或者说Z轴重合，具体原因后面会进一步分析，这里先记住这个重要的假设），从而使的镜面反射积分项整个与视见方向 ω⃗o\vec{\omega}_oωo​ 无关，进而可以做预积分处理。

  当然这样假设对于实际最终的画质效果来说可能会有损失，但是如果它可以使整个积分计算不需要在帧循环中实时执行，那么效率提升将是非常明显的。而这样的假设之所以是画质与效率之间的比较好的一个折中的原因是因为如果微表面的法线都比较集中在平面点 p⃗\vec{p}p​ 处法线 n⃗\vec{n}n 的周围，或者说非常接近，那么 DGGXD_{GGX}DGGX​ 将有较大的取值，从而使得如果视方向等同于法线方向时，可以得到最大的镜面反射量。

  当然粗糙度参数也会影响镜面反射量的大小，但它本身是点 p⃗\vec{p}p​ 处的一个参数，与积分中的各种向量无关，可以使用别的方式来简化处理。

  在假设情况下时，角 θ与θh\theta 与 \theta_hθ与θh​ 之间就会有如下图所示的关系：

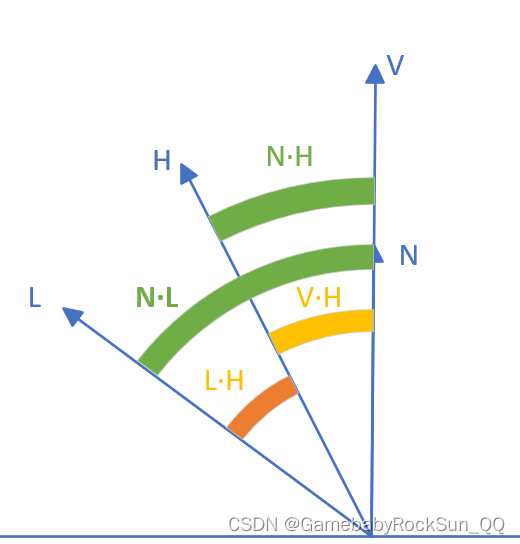
  首先图中的标识因为作图工具的原因，所以有些差别，其中 H=h⃗,N=n⃗,L=ω⃗i,V=ω⃗oH=\vec{h},N=\vec{n},L=\vec{\omega}_i,V=\vec{\omega}_oH=h,N=n,L=ωi​,V=ωo​ , 而且 L,V,H,NL,V,H,NL,V,H,N 的标识法也是一些其它资料中常用的标识，所以这里请大家记住他们各自本身的含义即可，具体符号标识只是一种表达习惯而已。

  那么由图中的信息我们立刻可以知道 θ=2θh\theta = 2\theta_hθ=2θh​ ，这也就是 h⃗\vec{h}h 被称为中间向量的本质含义而已。并且根据反射定律有 ϕ=ϕh(共面)\phi = \phi_h \ (共面)ϕ=ϕh​ (共面) 。

  当然 θ与θh\theta 与 \theta_hθ与θh​ 之间的这个简单关系与视向量和法线不对齐的情况是有区别的，所以我们使用带 * 号的标识加以区别，即 θ∗=2θh∗\theta^{*} = 2 \theta_h^{*}θ∗=2θh∗​。接着我们来继续推导：
∫ΩhDFG4(ωo⃗⋅n⃗)(ωi⃗⋅n⃗)Li(p⃗)cos⁡(θ)sin⁡(θ∗)dϕ⋅dθ∗sin⁡(θh∗)dϕh⋅dθh∗dωh=∫ΩhDFG4(ωo⃗⋅n⃗)(ωi⃗⋅n⃗)Li(p⃗)cos⁡(θ)sin⁡(2θh∗)dϕh⋅2dθh∗sin⁡(θh∗)dϕh⋅dθh∗dωh分子分母约分掉相同微分，并且∵sin⁡(2x)=2sin⁡(x)cos⁡(x)∴=∫ΩhDFG4(ωo⃗⋅n⃗)(ωi⃗⋅n⃗)Li(p⃗)cos⁡(θ)2×sin⁡(θh∗)×cos⁡(θh∗)×2sin⁡(θh∗)dωh接着又∵ω⃗i⋅n⃗=cos⁡(θ)此时进一步约分化简后有：=∫ΩhDFG(ωo⃗⋅n⃗)Li(p⃗)cos⁡(θh∗)dωh根据刚才的假设，此时有:cos⁡(θh∗)=ω⃗o⋅h⃗,dωh=sin⁡(θh)dθhdϕh∴=∫ΩhDFG(ωo⃗⋅n⃗)Li(p⃗)×(ω⃗o⋅h⃗)×sin⁡(θh)dθhdϕh\mathop{\int}_{\Omega_h} \frac{DFG}{4 ( \vec{\omega_o} \cdot \vec{n} ) (\vec{\omega_i} \cdot \vec{n} ) } \mathrm{L}_i(\vec{p}) \cos(\theta) \cfrac{\sin(\theta^*)\mathrm{d}\phi \cdot \mathrm{d}\theta^*}{\sin(\theta_h^*)\mathrm{d}\phi_h \cdot \mathrm{d}\theta_h^*} \mathrm{d} \omega_h \\[2ex] = \mathop{\int}_{\Omega_h}\frac{DFG}{4 ( \vec{\omega_o} \cdot \vec{n} ) (\vec{\omega_i} \cdot \vec{n} ) } \mathrm{L}_i(\vec{p}) \cos(\theta) \cfrac{\sin(2\theta_h^*) \mathrm{d}\phi_h \cdot 2 \mathrm{d}\theta_h^*}{\sin(\theta_h^*)\mathrm{d}\phi_h \cdot \mathrm{d}\theta_h^*} \mathrm{d} \omega_h \\[2ex] 分子分母约分掉相同微分，并且\because \quad \sin(2x) = 2 \sin(x) \cos(x) \\[2ex] \therefore \quad = \mathop{\int}_{\Omega_h}\frac{DFG}{4 ( \vec{\omega_o} \cdot \vec{n} ) (\vec{\omega_i} \cdot \vec{n} ) } \mathrm{L}_i(\vec{p}) \cos(\theta) \cfrac{2 \times \sin(\theta_h^*) \times \cos(\theta_h^*) \times 2 }{\sin(\theta_h^*) } \mathrm{d} \omega_h \\[2ex] 接着又\because \quad \vec{\omega}_i \cdot \vec{n} = \cos(\theta) \quad 此时进一步约分化简后有： \\[2ex] = \mathop{\int}_{\Omega_h} \frac{DFG}{ ( \vec{\omega_o} \cdot \vec{n} )} \mathrm{L}_i(\vec{p}) \cos(\theta_h^*) \mathrm{d} \omega_h \\[2ex] 根据刚才的假设，此时有: \cos(\theta_h^*) = \vec{\omega}_o \cdot \vec{h} , \mathrm{d} \omega_h = \sin(\theta_h) \mathrm{d} \theta_h \mathrm{d} \phi_h \\[2ex] \therefore \quad = \mathop{\int}_{\Omega_h}\frac{DFG}{ ( \vec{\omega_o} \cdot \vec{n} )} \mathrm{L}_i(\vec{p}) \times (\vec{\omega}_o \cdot \vec{h}) \times \sin(\theta_h) \mathrm{d} \theta_h \mathrm{d} \phi_h ∫Ωh​​4(ωo​​⋅n)(ωi​​⋅n)DFG​Li​(p​)cos(θ)sin(θh∗​)dϕh​⋅dθh∗​sin(θ∗)dϕ⋅dθ∗​dωh​=∫Ωh​​4(ωo​​⋅n)(ωi​​⋅n)DFG​Li​(p​)cos(θ)sin(θh∗​)dϕh​⋅dθh∗​sin(2θh∗​)dϕh​⋅2dθh∗​​dωh​分子分母约分掉相同微分，并且∵sin(2x)=2sin(x)cos(x)∴=∫Ωh​​4(ωo​​⋅n)(ωi​​⋅n)DFG​Li​(p​)cos(θ)sin(θh∗​)2×sin(θh∗​)×cos(θh∗​)×2​dωh​接着又∵ωi​⋅n=cos(θ)此时进一步约分化简后有：=∫Ωh​​(ωo​​⋅n)DFG​Li​(p​)cos(θh∗​)dωh​根据刚才的假设，此时有:cos(θh∗​)=ωo​⋅h,dωh​=sin(θh​)dθh​dϕh​∴=∫Ωh​​(ωo​​⋅n)DFG​Li​(p​)×(ωo​⋅h)×sin(θh​)dθh​dϕh​
  至此我们完成了所有的换元，将关于 θ,ϕ\theta,\phiθ,ϕ 的所有函数及微分都变成了关于 θh,ϕh\theta_h,\phi_hθh​,ϕh​ 的相应元素，并且简化了积分中的整个函数项。 这样我们就可以进一步根据我们设计的概率密度函数来进行蒙特卡洛积分了，当然根据我们对漫反射积分的处理如法炮制就行了：
∫abf(x)dx≈1N∑n=1Nf(xn)p(xn)⇒Los(p⃗,ωo⃗)≈1N∑n=1NDFG(ωo⃗⋅n⃗)Li(p⃗)×(ω⃗o⋅h⃗)×sin⁡(θh)DGGXcos⁡(θh)sin⁡(θh)=1N∑n=1NFG×(ω⃗o⋅h⃗)(ωo⃗⋅n⃗)×cos⁡(θh)Li(p⃗)=1N∑n=1NFG×(ω⃗o⋅h⃗)(ωo⃗⋅n⃗)×(n⃗⋅h⃗)Li(p⃗)\int \limits_a^b {f}(x) \mathrm{d} x \approx \cfrac{1}{N} \sum \limits_{n=1}^{N} \cfrac{{f}(x_n)}{\mathrm{p}(x_n)} \\[2ex] \Rightarrow \mathrm{L}_{o_s}(\vec{p},\vec{\omega_{o}}) \approx \cfrac{1}{N} \sum \limits_{n=1}^{N} \cfrac{ \frac{DFG}{ ( \vec{\omega_o} \cdot \vec{n} )} \mathrm{L}_i(\vec{p}) \times (\vec{\omega}_o \cdot \vec{h}) \times \sin(\theta_h) } {D_{GGX} \cos(\theta_h) \sin(\theta_h) } \\[2ex] = \cfrac{1}{N} \sum \limits_{n=1}^{N} \cfrac{FG\times (\vec{\omega}_o \cdot \vec{h})} {( \vec{\omega_o} \cdot \vec{n} ) \times \cos(\theta_h)} \mathrm{L}_i(\vec{p}) \\[2ex] = \cfrac{1}{N} \sum \limits_{n=1}^{N} \cfrac{FG\times (\vec{\omega}_o \cdot \vec{h})} {( \vec{\omega_o} \cdot \vec{n} ) \times (\vec{n} \cdot \vec{h})} \mathrm{L}_i(\vec{p}) a∫b​f(x)dx≈N1​n=1∑N​p(xn​)f(xn​)​⇒Los​​(p​,ωo​​)≈N1​n=1∑N​DGGX​cos(θh​)sin(θh​)(ωo​​⋅n)DFG​Li​(p​)×(ωo​⋅h)×sin(θh​)​=N1​n=1∑N​(ωo​​⋅n)×cos(θh​)FG×(ωo​⋅h)​Li​(p​)=N1​n=1∑N​(ωo​​⋅n)×(n⋅h)FG×(ωo​⋅h)​Li​(p​)

  这样我们就推导出了镜面反射项的蒙特卡洛积分形式，并且如预期的我们也消去了 DGGXD_{GGX}DGGX​ 函数（大家可以想想为啥不干脆把 G函数 F函数 都拉进概率密度函数，然后全部消掉呢？）。

  同时根据前面的步骤以及推导，我们还有：
θh=arccos⁡(1−μμ(α2−1)+1)ϕh=2πνh⃗=[sin⁡(θh)cos⁡(ϕh)sin⁡(θh)sin⁡(θh)cos⁡(θh)]ω⃗i=2×(ω⃗o⋅h⃗)×h⃗−ω⃗o\theta_h = \arccos \left( \sqrt{\cfrac{1-\mu}{\mu (\alpha^2 - 1 ) + 1}} \right) \\[2ex] \phi_h = 2 \pi \nu \\[2ex] \vec{h} = \begin{bmatrix} \sin(\theta_h)\cos(\phi_h) \\ \sin(\theta_h) \sin(\theta_h) \\ \cos(\theta_h) \end{bmatrix} \\[2ex] \vec{\omega}_i = 2 \times (\vec{\omega}_o \cdot \vec{h}) \times \vec{h} - \vec{\omega}_o θh​=arccos​μ(α2−1)+11−μ​​​ϕh​=2πνh=​sin(θh​)cos(ϕh​)sin(θh​)sin(θh​)cos(θh​)​​ωi​=2×(ωo​⋅h)×h−ωo​

  至此我们可以发现，积分中的向量，只剩下视见向量 ω⃗o\vec{\omega}_oωo​ 暂时还没有办法计算了。让我们继续努力！