文章目录

• 改造红黑树
• • 1.红黑树节点的改造
  • 2.红黑树模板参数的改造
  • 3.红黑树插入的改造
• 红黑树迭代器的实现
• • 迭代器的结构
  • 迭代器的构造函数
  • operator*和operator->的实现
  • operator!=的实现
  • operator++(前置)的实现
  • operator++(后置)的实现
  • operator--(前置)的实现
  • operator--(后置)的实现
• 红黑树封装实现map和set的整体代码
• • RBtree.h
  • Myset.h
  • Mymap.h

改造红黑树

要用红黑树实现map和set的时候，我们面临一个问题。
看一下代码：

红黑树的节点结构我们是这么实现的，而节点里面存的数据类型是pari对象。
根据之前学习和使用过map和set的时候我们知道，set节点里面存的数据是一个K类型，而map节点里面存的一个数据是一个pari对象。那么我们如何让一颗树满足两个容器呢？

可以进行以下改造：

1.红黑树节点的改造

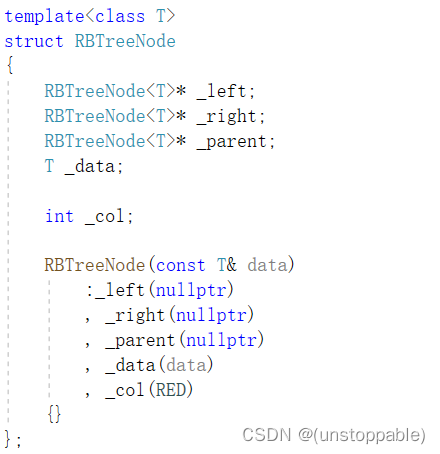
既然我们不知道会传的是什么类型的数据，我们就直接把模板参数的改成T，我们在外面封装实现set和map的时候显示传就可以。

2.红黑树模板参数的改造

原模板参数：

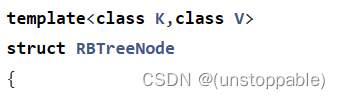
改造后的模板参数：

模板里的KeyOfT下面再讲解，这里先跳过
set：

map：

3.红黑树插入的改造

原插入的参数：

改造后插入的参数：

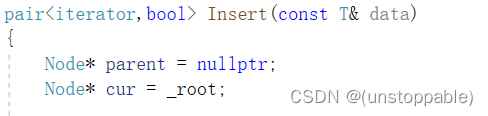
改造后的插入函数的返回值我们下面再讲解，这里先跳过。

改造后我们又遇到难题了，我们知道红黑树也是二叉搜索树，遵循二叉搜索树的规则，新插入节点时，要进行节点之间的比较，新节点的值比节点的值大往右走，比节点的值小往左走。但是我们传了个T过来，我们也不知道它是pair，还是K。我们要如何比较？
这我们运用到了仿函数，底层红黑树是不知道，但是外层封装的map和set知道啊，所以我们在set和map中分别写出它们各自的仿函数，然后显示的传给红黑树.
set:


map:

改造前的插入代码：

改造后的插入新节点：

从图片的代码中我们可以看出，每当我们要进行两个节点的比较之前，我们要定义一个KeyOfT的kot对象，然后用它们的返回值进行比较。

到这里我们改造的就差不多了，其它的几乎不用怎么变，解下来最重要的就是实现红黑树的迭代器。

红黑树迭代器的实现

迭代器是C++ STL库中所有数据结构容器必须实现的一个。
它是对节点指针的封装，让所有数据结构容器可以像指针一样去实现用迭代器的++或者–来实现遍历。

迭代器的结构

迭代器的构造函数

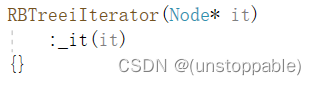
operator*和operator->的实现

operator!=的实现

operator++(前置)的实现

红黑树迭代器的精华就是，它的++和–的实现。我们知道对数组我们可以使用原生指针的++、--和解引用来对数组进行遍历，但是对于红黑树我们就不能使用原生指针的++、--来对树形结构进行遍历。因为数组底层存储数据的空间是连续的，而红黑树底层存储数据的空间是不连续的。
那么我们如何让红黑树像数组一样去用指针的++、–来遍历红黑树呢？

我们知道，红黑树的中序遍历是有序的，所以我们用迭代器遍历时，就遵循中序遍历的思想。
中序遍历思想：
先访问左子树
再访问根
最后访问右子树

所以当对一个红黑树的节点指针++,如果该节点的右子树存在，那么下一个访问的就是右子树最左的节点的值。如果右子树不存在，那么说明我存在的子树已经访问完了，那么继续沿着到根节点的路径找孩子是父亲左的那个节点，下一个访问的就是这个节点的值。


整颗树都访问完了的情况：

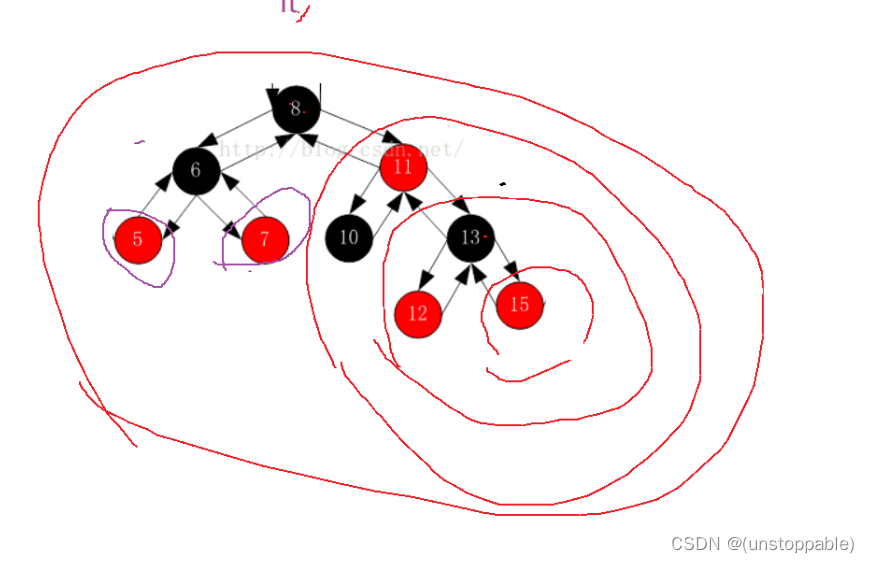
首先我们传的是15这个节点的指针，我们会发现15的右子树为空。

说明15的右子树已经访问完毕，沿着根路径走找到了13，我们发现15是13的右节点。

说明13的右子树已经访问完毕，我们继续沿着根路走找到了11，我们发现13是11的右节点。

说明11的右子树已经访问完毕我们继续沿着根路走找到了8，而11又是8的右节点，我们继续沿着根路走到了空。

说明整颗树已经访问完毕。

operator++(后置)的实现

后置++的实现和前置++的实现是一样的，只不过是返回值的区别。
这里如果不理解前置++和后置++的区别，大家可以自己去理解一下。

后置++的返回是传值返回，因为后置++要返回的是++前的迭代器，而迭代++后指向的位置就变了，所以我们对这个迭代器提前用来一个临时迭代器来保存，我们最后返回的是这个临时迭代器，但是出了作用域这个迭代器就不存在了，所以我们不能传引用返回，只能传值返回。

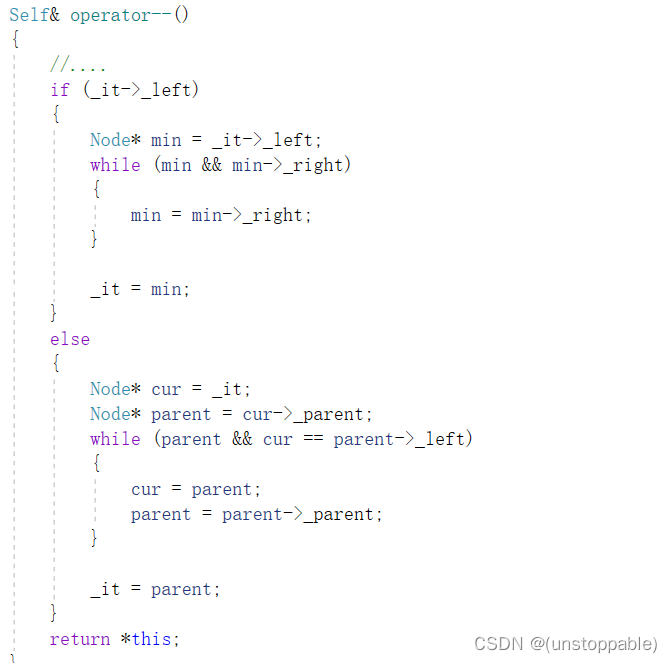
operator–(前置)的实现

–的思路和++的思路是一样的。
当对一个红黑树的节点指针--,如果该节点的左子树存在，那么下一个访问的就是左子树最右的节点的值。如果左子树不存在，那么说明我存在的子树已经访问完了，那么继续沿着到根节点的路径找孩子是父亲右的那个节点，下一个访问的就是这个节点的值。

operator–(后置)的实现

后置–的实现和前置–的实现是一样的，只不过是返回值的区别。
这里如果不理解前置++和后置++的区别，大家可以自己去理解一下。

后置–的传值返回和后置++传值返回的原因一样这里就不过多赘述。

下面我们将继续讲解前面预留的一个问题，插入的返回值为什么是一个pari?
因为STL的map支持operator[],而这个运算符的作用大家应该也知道，不理解的伙伴可以看我之前写的博客。这里就不过多讲述。

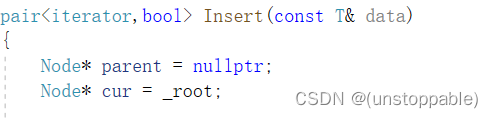
这里就是为了支持[ ]可以修改kv.second，所以支持了pair对象返回.

红黑树封装实现map和set的整体代码

RBtree.h

#pragma once
namespace lzf
{enum Colour{RED,BLACK};templatestruct RBTreeNode{RBTreeNode* _left;RBTreeNode* _right;RBTreeNode* _parent;T _data;int _col;RBTreeNode(const T& data):_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _col(RED){}};templatestruct RBTreeiIterator{private:typedef RBTreeNode Node;typedef RBTreeiIterator Self;public:RBTreeiIterator(Node* it):_it(it){}Ref operator*(){return _it->_data;}Ptr operator->(){return &_it->_data;}bool operator!=(const Self& it){return _it != it._it;}Self& operator++(){//....if (_it->_right){Node* min = _it->_right;while (min && min->_left){min = min->_left;}_it = min;}else{Node* cur = _it;Node* parent = cur->_parent;while (parent && cur == parent->_right){cur = parent;parent = parent->_parent;}_it = parent;}return *this;}Self operator++(int){//....Self temp(_it);if (_it->_right){Node* min = _it->_right;while (min && min->_left){min = min->_left;}_it = min;}else{Node* cur = _it;Node* parent = cur->_parent;while (parent && cur == parent->_right){cur = parent;parent = parent->_parent;}_it = parent;}return temp;}Self& operator--(){//....if (_it->_left){Node* min = _it->_left;while (min && min->_right){min = min->_right;}_it = min;}else{Node* cur = _it;Node* parent = cur->_parent;while (parent && cur == parent->_left){cur = parent;parent = parent->_parent;}_it = parent;}return *this;}Self operator--(int){//....Self temp(_it);if (_it->_left){Node* min = _it->_left;while (min && min->_right){min = min->_right;}_it = min;}else{Node* cur = _it;Node* parent = cur->_parent;while (parent && cur == parent->_left){cur = parent;parent = parent->_parent;}_it = parent;}return temp;}private:Node* _it;};//set RBTree//map RBTree>templateclass RBTree{typedef RBTreeNode Node;public:typedef RBTreeiIterator iterator;iterator begin(){Node* min = _root;while (min && min->_left){min = min->_left;}return iterator(min);}iterator end(){return iterator(nullptr);}RBTree():_root(nullptr){}RBTree(const RBTree& t){_root = Copy(t._root);}~RBTree(){Destory(_root);_root = nullptr;}iterator Find(const K& key){Node* cur = _root;KeyOfT kot;while (cur){if (kot(cur->_data) < key){cur = cur->_right;}else if (kot(cur->_data) > key){cur = cur->_left;}else{return iterator(cur);}}return end();}RBTree&  operator=(RBTree t){swap(_root, t._root);return *this;}pair Insert(const T& data){Node* parent = nullptr;Node* cur = _root;//如果根为空if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return make_pair(iterator(_root),true);}KeyOfT kot;//寻找插入位置while (cur){//如果要插入的值比cur的值小if (kot(cur->_data) > kot(data)){//往左找parent = cur;cur = cur->_left;}//如果要插入的值比cur的值大else if (kot(cur->_data) < kot(data)){//往右找parent = cur;cur = cur->_right;}//如果相等就不再插入else{return make_pair(iterator(cur), true);}}//插入cur = new Node(data);Node* node = cur;if (kot(parent->_data) > kot(data)){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}//更新颜色while (parent && parent->_col == RED){Node* grandpa = parent->_parent;Node* uncle = nullptr;if (grandpa->_left == parent){uncle = grandpa->_right;if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandpa->_col = RED;cur = grandpa;parent = cur->_parent;}else{//单旋if (parent->_left == cur){RotateR(grandpa);parent->_col = BLACK;grandpa->_col = RED;}//双旋else{RotateLR(grandpa);grandpa->_col = RED;cur->_col = BLACK;}break;}}else{uncle = grandpa->_left;if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandpa->_col = RED;cur = grandpa;parent = cur->_parent;}else{//单旋if (parent->_right == cur){RotateL(grandpa);parent->_col = BLACK;grandpa->_col = RED;}//双旋else{RotateRL(grandpa);cur->_col = BLACK;grandpa->_col = RED;}break;}}}_root->_col = BLACK;return make_pair(iterator(node), true);}private:void RotateR(Node* parent){//要调整的节点Node* sub = parent;//要调整的节点的左孩子Node* subL = parent->_left;//要调整的节点的左孩子的右孩子Node* subLR = subL->_right;//要调整的节点的父母Node* subparent = sub->_parent;//重新链接关系if (subLR)subLR->_parent = sub;sub->_left = subLR;sub->_parent = subL;subL->_right = sub;subL->_parent = subparent;if (_root == sub){_root = subL;}else{if (subparent->_left == sub){subparent->_left = subL;}else{subparent->_right = subL;}}}void RotateL(Node* parent){//要调整的节点Node* sub = parent;//要调整的节点的右孩子Node* subR = parent->_right;//要调整的节点的有孩子的左孩子Node* subRL = subR->_left;//要调整的节点的父母Node* subparent = sub->_parent;//重新链接关系if (subRL)subRL->_parent = sub;sub->_right = subRL;sub->_parent = subR;subR->_left = sub;subR->_parent = subparent;if (_root == sub){_root = subR;}else{if (subparent->_left == sub){subparent->_left = subR;}else{subparent->_right = subR;}}}void RotateRL(Node* parent){RotateR(parent->_right);RotateL(parent);}void RotateLR(Node* parent){RotateL(parent->_left);RotateR(parent);}void Destory(Node* root){if (root == nullptr){return;}Destory(root->_left);Destory(root->_right);delete root;}Node* Copy(Node* root){if (root == nullptr){return nullptr;}Node* newnode = new Node(root->_data);newnode->_col = root->_col;newnode->_left = Copy(root->_left);newnode->_right = Copy(root->_right);if (newnode->_left)newnode->_left->_parent = newnode;if (newnode->_right)newnode->_right->_parent = newnode;return newnode;}private:Node* _root;};}

Myset.h

#pragma once
#include"RBTree.h"
namespace lzf
{templateclass MySet{struct SetKeyOfT{const K& operator()(const K& k){return k;}};public:typedef typename lzf::RBTree::iterator iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}pair Insert(const K& data){return _t.Insert(data);}iterator find(const K& k){return _t.Find(k);}private://setlzf::RBTree _t;};void Test_Set(){MySet s;s.Insert(1);s.Insert(2);s.Insert(3);s.Insert(4);s.Insert(5);s.Insert(6);MySet::iterator it = s.begin();while (it != s.end()){cout << *it << " ";++it;}cout << endl;MySet s1(s);MySet::iterator it1 = s1.begin();while (it1 != s1.end()){cout << *it1 << " ";++it1;}cout << endl;MySet::iterator it2 = s1.find(5);cout << *it2;}
}

Mymap.h

#pragma once
#include"RBTree.h"
namespace lzf
{templateclass MyMap{struct MapKeyOfT{const K& operator()(const pair& kv){return kv.first;}};public:typedef typename lzf::RBTree, MapKeyOfT>::iterator iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}pair Insert(const pair& data){return _t.Insert(data);}V& operator[](const K& k){auto ret = _t.Insert(make_pair(k, V()));return ret.first->second;}iterator find(const K& k){return _t.Find(k);}private://maplzf::RBTree, MapKeyOfT> _t;};void Test_Map(){MyMap m;m.Insert(make_pair(1, 1));m.Insert(make_pair(2, 2));m.Insert(make_pair(3, 3));m.Insert(make_pair(4, 4));MyMap::iterator it = m.begin();while (it != m.end()){cout << it->first<<":"<second << endl;++it;}cout << endl;MyMap m1;m1["sort"];m1["sort"] = "排序";m1["left"] = "左边";m1["map"] = "地图";m1["son"] = "儿子";m1["map"] = "地图、映像";MyMap::iterator it1 = m1.begin();while (it1 != m1.end()){cout << it1->first << ":" << it1->second << endl;++it1;}cout << endl;}
}