文章目录

• 一、正文
• • • 1. 星座图
    • 2. 眼图
    • 8.2.3 增益、延迟和信噪比
• 二、附录

一、正文

在编译时出现了一个小问题，我的 .M 文件无法正常打开，显示是不受支持的 MATLAB 代码，后来我重新定义为小写的 .m 文件，问题得到了解决。

当然，另一种解决方案是将函数内容直接写道主函数里面，此处不表。

k = menu('pi/4 QPSK Plot Options',...'Unfiltered pi/4 QPSK Signal Constellation',...'Unfiltered pi/4 QPSK Eye Diagram',...'Filtered pi/4 QPSK Signal Constellation',...'Filtered pi/4 OQPSK Eye Diagram',...'Unfiltered Direct and Quadrature Signals',...'Filtered Direct and Quadrature Signals',...'Exit Program');

这段代码创建了一个菜单，其中包含了7个选项，每个选项对应一个图形的类型。用户可以通过选择不同的选项来查看不同的图形。如果选择“Exit Program”，则程序将退出。

menu函数参数表中的 “…” 有什么用？

在这里，“…” 的作用是让你可以在同一个 menu 函数调用中提供多个选项，而不需要在同一行中输入所有选项。

%
% set direct and quadrature bit streams
%
data = round(rand(1,bits));
dd = data(1:2:bits-1);
qq = data(2:2:bits);

串井转换器交替将（奇序数的）符号分配给同相信道，将其他（偶序数的）符号分配给正交信道，千是有

a(1)a(2)a(3)a(4)⋯a(k)⋯=d(1)q(1)d(2)q(2)⋯d(k+12)q(k2+1)⋯a(1) a(2) a(3) a(4) \cdots a(k) \cdots=d(1) q(1) d(2) q(2) \cdots d\left(\frac{k+1}{2}\right) q\left(\frac{k}{2}+1\right) \cdots a(1)a(2)a(3)a(4)⋯a(k)⋯=d(1)q(1)d(2)q(2)⋯d(2k+1​)q(2k​+1)⋯

这段代码是用随机数生成一个长度为bits的二进制数据流，并将其分成了直接通道（dd）和象限通道（qq）两个部分。其中dd包含了数据流中的奇数位，qq包含了数据流中的偶数位。这个过程是为了将二进制数据流转换成复数信号，以便进行QPSK调制。

theta(1) = iphase;						% set initial phase
thetaout(1:sps) = theta(1)*ones(1,sps);

θ(k)=θ(k−1)+ϕ(k)\theta(k)=\theta(k-1)+\phi(k) θ(k)=θ(k−1)+ϕ(k)

for k=2:mif dd(k) == 1phi_k = (2*qq(k)-1)*pi/4;elsephi_k = (2*qq(k)-1)*3*pi/4;endtheta(k) = phi_k + theta(k-1);for i=1:spsj = (k-1)*sps+i;thetaout(j) = theta(k);end
endd = cos(thetaout);
q = sin(thetaout);

这一段代码是有问题的，因为教材P195 说的很清楚，且初始相位定义为 θ(0)=0\theta(0)=0θ(0)=0。按照上面 MATLAB 代码的写法，dd(1)和qq(1)是永远用不到的。我们知道就好，不影响整体程序的运行“应该”。

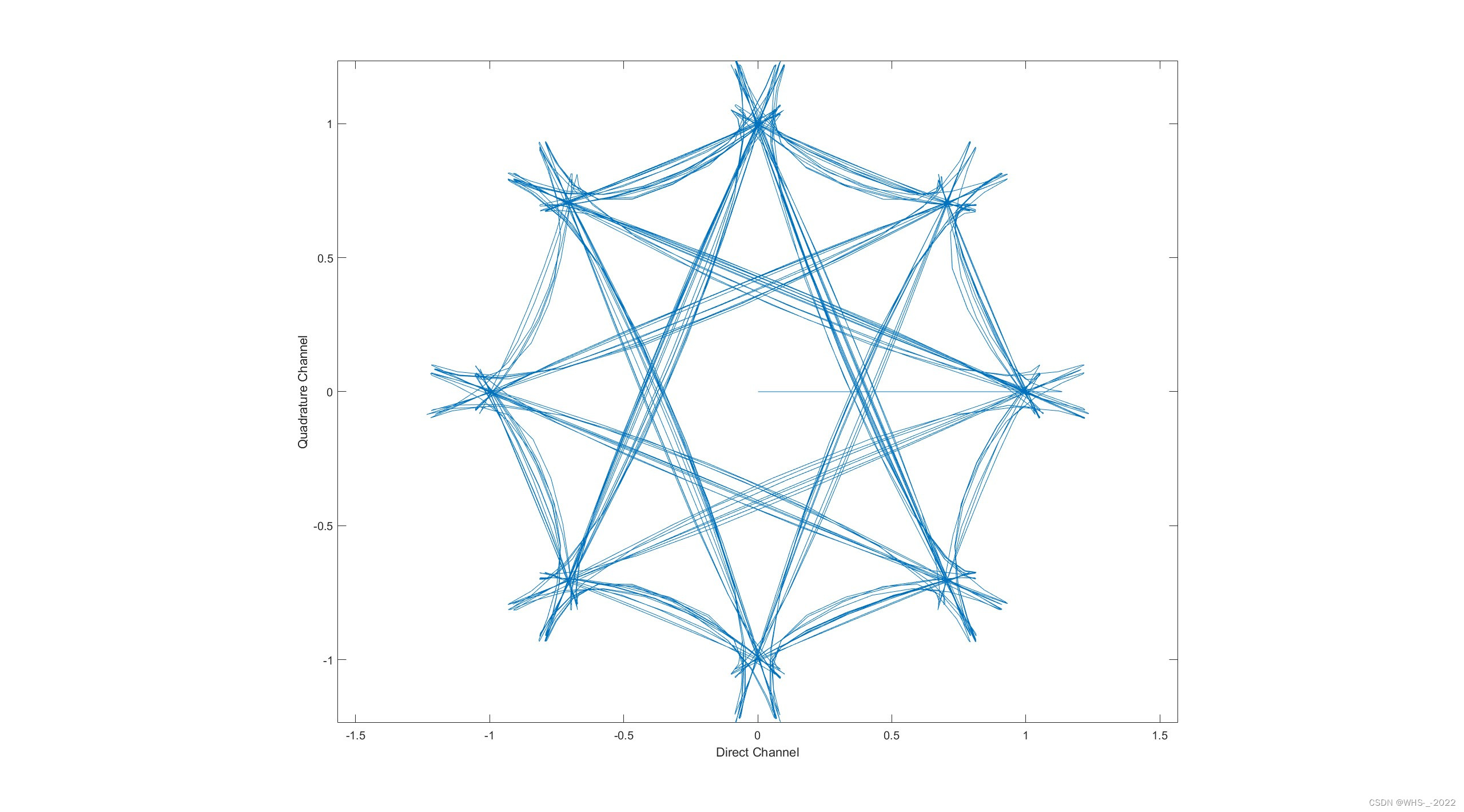
1. 星座图

% File: sigcon.m
% Software given here is to accompany the textbook: W.H. Tranter,
% K.S. Shanmugan, T.S. Rappaport, and K.S. Kosbar, Principles of
% Communication Systems Simulation with Wireless Applications,
% Prentice Hall PTR, 2004.
% 
function []=sigcon(x,y)
plot(x,y);
axis('square')
axis('equal')
xlabel('Direct Channel')
ylabel('Quadrature Channel')
end
% End of function file.

x表示同相信号，y表示正交信号。

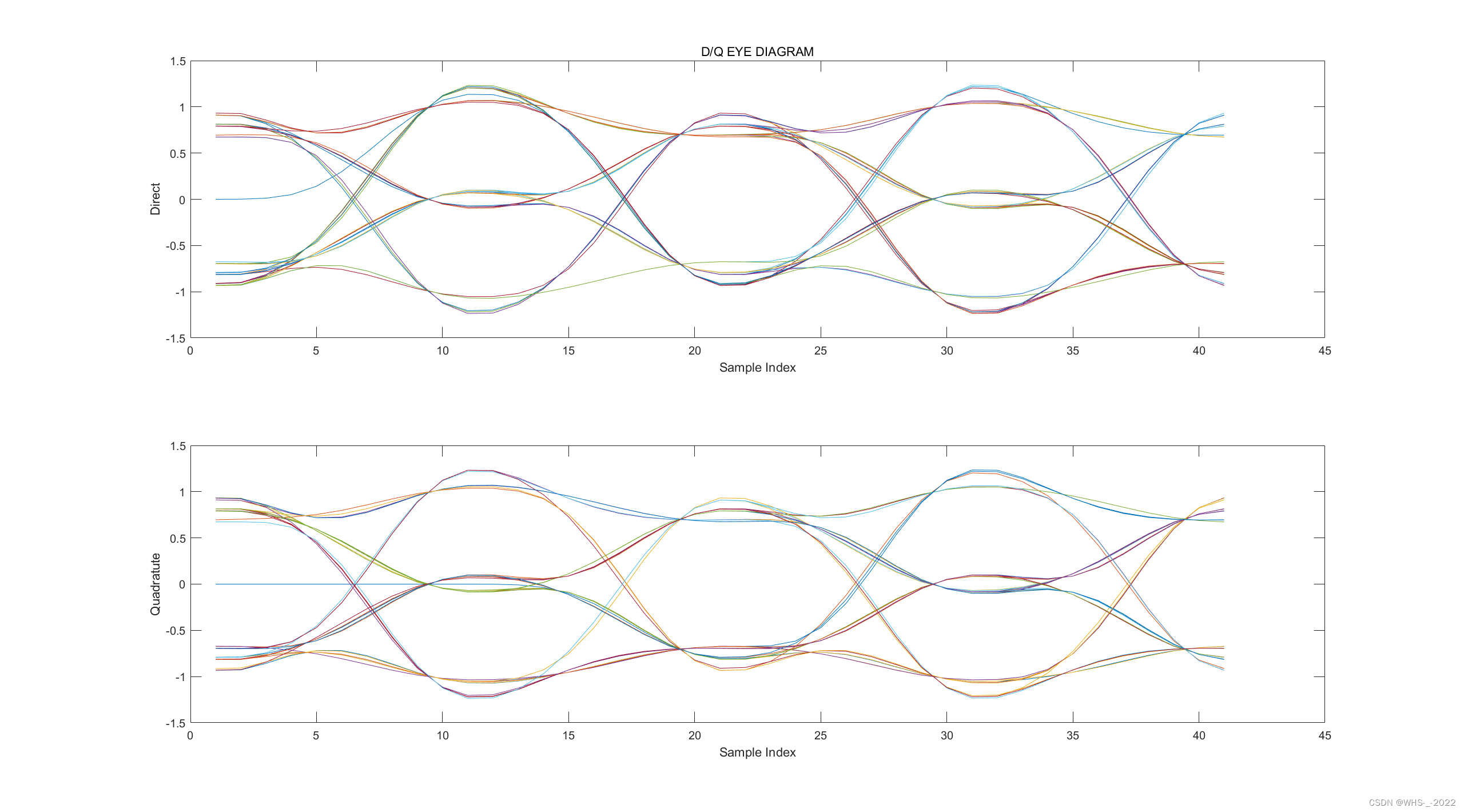
2. 眼图

% File: dqeye.m
% Software given here is to accompany the textbook: W.H. Tranter,
% K.S. Shanmugan, T.S. Rappaport, and K.S. Kosbar, Principles of
% Communication Systems Simulation with Wireless Applications,
% Prentice Hall PTR, 2004.
%
% plot unfiltered eye diagram
%xd是同相信号，xq是正交信号，m在主程序中是4*sps=40
function [] = dqeye(xd,xq,m)
lx = length(xd);                % samples in data segment，选取200个symbol,每个symbol取10个点，lx=2000
kcol = floor(lx/m);             % number of columns
xda = [0,xd]; xqa = [0,xq];     % append zeros,默认初始相位是0
for j = 1:kcol                  % column indexfor i = 1:(m+1)             % row indexkk = (j-1)*m+i;         % sample indexy1(i,j) = xda(kk);y2(i,j) = xqa(kk);end
endsubplot(211)                    % direct channel
plot(y1);
title('D/Q EYE DIAGRAM');
xlabel('Sample Index');
ylabel('Direct');subplot(212)                    % quadrature channel
plot(y2);
xlabel('Sample Index');
ylabel('Quadratute');
subplot(111)                    % restore
% End of function file.

对plot(y2); 的一点解释:

在Matlab中，当使用plot(a)绘制一个矩阵时，Matlab会自动将该矩阵的每一列视为一个向量，并将其绘制在一个单独的坐标系上，横坐标默认为该列在矩阵中的 row 索引，纵坐标则为该列的值。因此，对于一个40*50的矩阵，Matlab会绘制出50条线段，每条线段有40个点，横坐标分别为1到40。

眼图这里的代码有点难以理解，我来做一点解释。

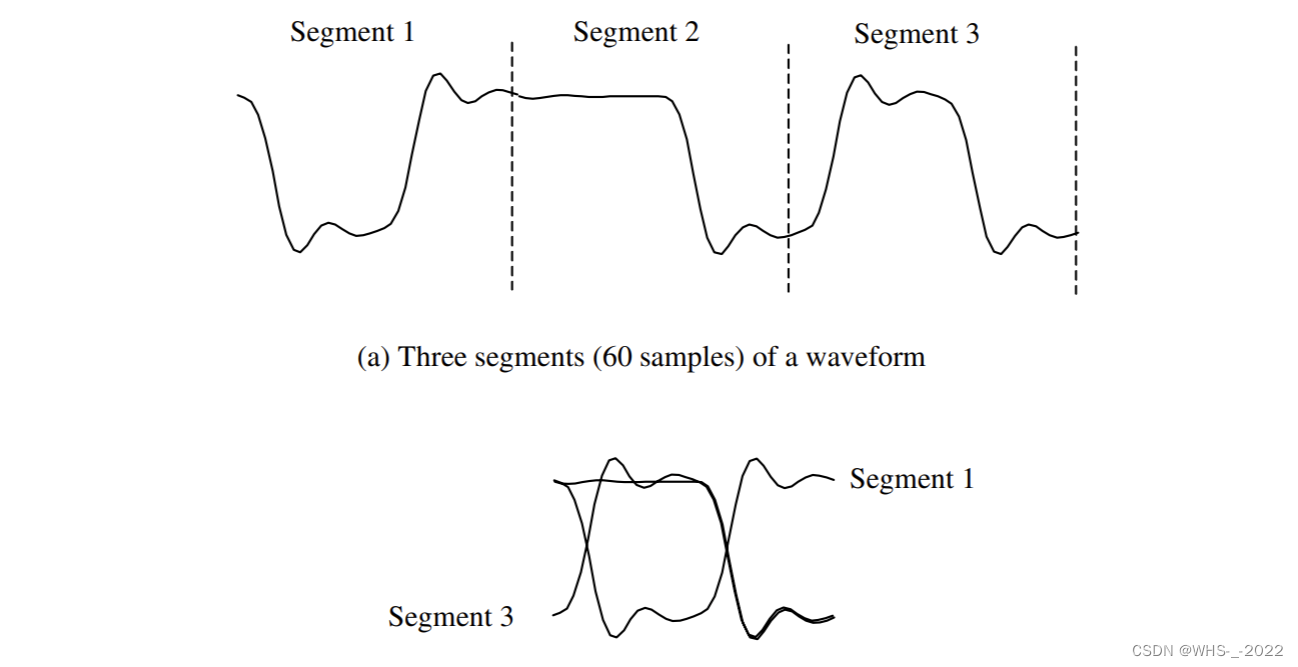
d = cos(thetaout);
q = sin(thetaout);elseif k ==2dqeye(d,q,4*sps)        	% plot unfiltered eye diagrampause

我们通过上面这个代码得到的d和q实际上是 1×20001\times 20001×2000 的向量，选取200个symbol,每个symbol取10个点，lx=2000。那上图中一个 Segment 在程序中我们取 4*sps，如下图示意。

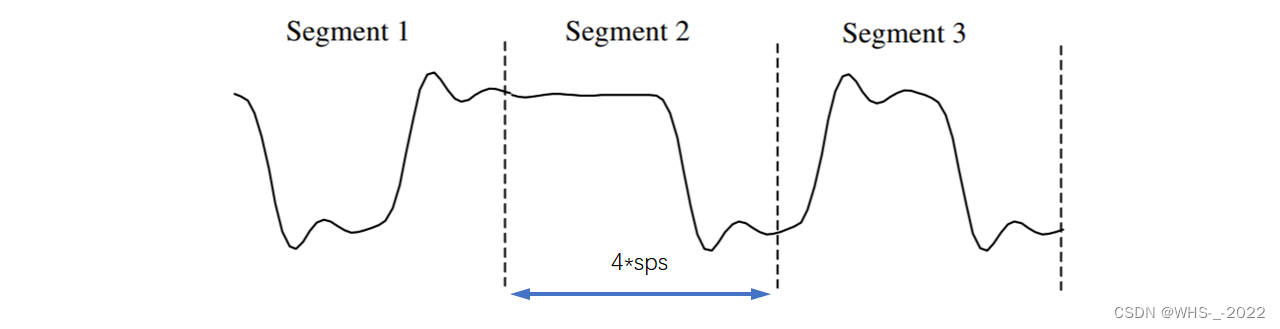
但是如果真的取4*sps画图的话，因为我们这里是模拟仿真，会发现眼图是恰好会重合在一起，为了示意眼图，我们用下面的方式排列矩阵并且绘图，就能得到正确的眼图了。

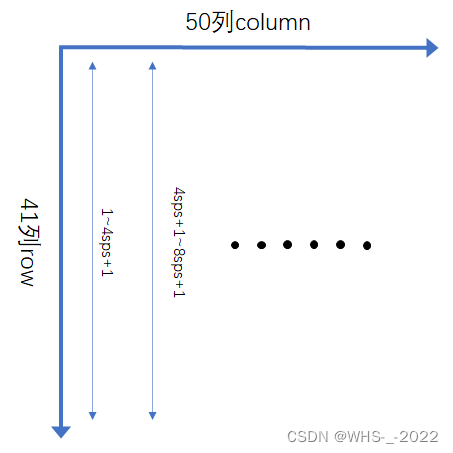
8.2.3 增益、延迟和信噪比

实低通信号的理论推导

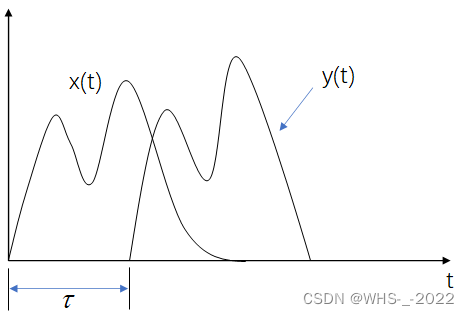
对线性时不变无失真系统，系统中任意点信号 y(t)y(t)y(t) 是对输入参考信号 x(t)x(t)x(t) 按幅度比例缩放并加入延迟后所得的信号。因此， 我们可以将无失真信号写为：

z(t)=Ax(t−τ)z(t)=A x(t-\tau)z(t)=Ax(t−τ)

其中， AAA 是增益， τ\tauτ 是系统中定义SNR的那个点的群时延。令 x(t)x(t)x(t) 为参考信号， y(t)y(t)y(t) 为观测信号，于是
y(t)=Ax(t−τ)+n(t)+d(t)(21)y(t)=A x(t-\tau)+n(t)+d(t)\tag{21}y(t)=Ax(t−τ)+n(t)+d(t)(21)

其中， n(t)n(t)n(t) 代表外部加性噪声， d(t)d(t)d(t) 是系统引人的跟信号相关的内部失真， 这种内部失真可能由码间千扰或非线性造成。描述系统中不同信号之间关系的方框图如图8-11 所示。

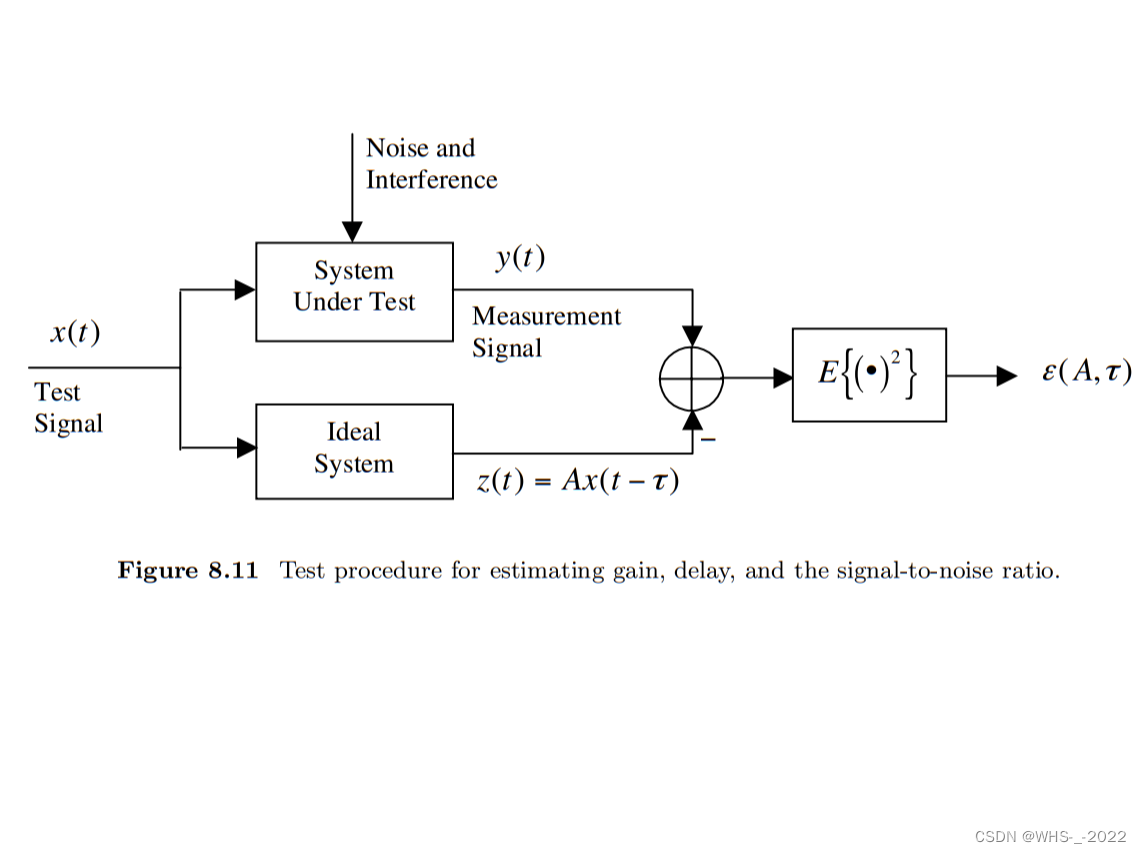
噪声功率定义为 y(t)y(t)y(t) 和无失真系统输出 z(t)=Ax(t−τ)z(t) = Ax(t -\tau)z(t)=Ax(t−τ)之间的MSE , 即：

ε(A,τ)=E{[y(t)−Ax(t−τ)]2}\varepsilon(A, \tau)=E\left\{[y(t)-A x(t-\tau)]^{2}\right\}ε(A,τ)=E{[y(t)−Ax(t−τ)]2}

AAA 和 τ\tauτ 理想估计值是最小化 ε(A,τ)\varepsilon(A, \tau)ε(A,τ)的值。上述表达式可写为：

ε(A,τ)=E{y2(t)+A2x2(t−τ)−2Ax(t−τ)y(t)}(23)\varepsilon(A, \tau)=E\left\{y^{2}(t)+A^{2} x^{2}(t-\tau)-2 A x(t-\tau) y(t)\right\}\tag{23}ε(A,τ)=E{y2(t)+A2x2(t−τ)−2Ax(t−τ)y(t)}(23)

对于平稳信号， 各阶矩独立于时间起点。此外， 和的期望等于期望的和，因此， 方程(8-23)可写为：
ε(A,τ)=E{y2(t)}+A2E{x2(t)}−2AE{x(t)y(t+τ)}(24)\varepsilon(A, \tau)=E\left\{y^{2}(t)\right\}+A^{2} E\left\{x^{2}(t)\right\}-2 A E\{x(t) y(t+\tau)\}\tag{24}ε(A,τ)=E{y2(t)}+A2E{x2(t)}−2AE{x(t)y(t+τ)}(24)

这里的 E{x(t)y(t+τ)}E\{x(t) y(t+\tau)\}E{x(t)y(t+τ)} 是求得最大的期望相关功率，在仿真时我们选择近似用 x(t)x(t)x(t) 的长度来代替时长。

因此，信噪比为

SN=Rxy2(τm)Px[PxPxPy−Rxy2(τm)]=Rxy2(τm)PxPy−Rxy2(τm)(30)\frac{S}{N}=\frac{R_{x y}^{2}\left(\tau_{m}\right)}{P_{x}}\left[\frac{P_{x}}{P_{x} P_{y}-R_{x y}^{2}\left(\tau_{m}\right)}\right]=\frac{R_{x y}^{2}\left(\tau_{m}\right)}{P_{x} P_{y}-R_{x y}^{2}\left(\tau_{m}\right)}\tag{30}NS​=Px​Rxy2​(τm​)​[Px​Py​−Rxy2​(τm​)Px​​]=Px​Py​−Rxy2​(τm​)Rxy2​(τm​)​(30)

x(t)x(t)x(t) 和 y(t)y(t)y(t) 的相关系数 ρ\rhoρ 定义为
ρ=Rxy(τm)PxPy(31)\rho=\frac{R_{x y}\left(\tau_{m}\right)}{\sqrt{P_{x} P_{y}}}\tag{31}ρ=Px​Py​​Rxy​(τm​)​(31)

根据这个定义，在测量点 y(t)y(t)y(t) 处， SNR的表达式很简单：
SN=ρ21−ρ2(32)\frac{S}{N}=\frac{\rho^{2}}{1-\rho^{2}}\tag{32}NS​=1−ρ2ρ2​(32)

我们都知道圆周卷积有这个公式
y(n)=[∑m=0L−1x1(m)∑r=−∞∞x2(n+rL−m)]RL(n)=[∑r=−∞∞∑m=0L−1x1(m)x2(n+rL−m)]RL(n)=[∑r=−∞∞yl(n+rL)]RL(n)\begin{aligned} y(n) & =\left[\sum_{m=0}^{L-1} x_{1}(m) \sum_{r=-\infty}^{\infty} x_{2}(n+r L-m)\right] \mathrm{R}_{\mathrm{L}}(n) \\ & =\left[\sum_{r=-\infty}^{\infty} \sum_{m=0}^{L-1} x_{1}(m) x_{2}(n+r L-m)\right] \mathrm{R}_{L}(n)\\ &=\left[\sum_{r=-\infty}^{\infty} y_{l}(n+r L)\right] R_{L}(n) \end{aligned} y(n)​=[m=0∑L−1​x1​(m)r=−∞∑∞​x2​(n+rL−m)]RL​(n)=[r=−∞∑∞​m=0∑L−1​x1​(m)x2​(n+rL−m)]RL​(n)=[r=−∞∑∞​yl​(n+rL)]RL​(n)​
我们知道圆周卷积有定义
rˉxy(m)=∑n=0N−1x(n)y((n−m))NRN(m)=∑n=0N−1x(n)y((−(m−n)))NRN(m)=x(m)N◯y(N−m)\begin{aligned} \bar{r}_{x y}(m) & =\sum_{n=0}^{N-1} x(n) y((n-m))_{N} R_{N}(m) \\ & =\sum_{n=0}^{N-1} x(n) y((-(m-n)))_{N} R_{N}(m)=x(m) \textcircled{N} y(N-m) \end{aligned} rˉxy​(m)​=n=0∑N−1​x(n)y((n−m))N​RN​(m)=n=0∑N−1​x(n)y((−(m−n)))N​RN​(m)=x(m)N◯y(N−m)​
那么必然圆周卷积也是线性相关的平移，即

rˉxy(m)=∑n=0N1−1x(n)y((n−m))NRN(m)=[∑n=0N1−1x(n)∑r=−∞∞y(n−m+rL)]RN(m)=[∑r=−∞∞∑n=0n=N1−1x(n)y(n−(m−rL))]RN(m)=[∑r=−∞∞rxy(n−rN)]RN(m)\begin{aligned} \bar{r}_{x y}(m) & =\sum_{n=0}^{N_1-1} x(n) y((n-m))_{N} R_{N}(m) \\ &=[\sum_{n=0}^{N_1-1} x(n) \sum_{r=-\infty}^{\infty}y(n-m+rL) ]R_{N}(m)\\ &=[\sum_{r=-\infty}^{\infty} \sum_{n=0}^{n=N_1-1}x(n)y(n-(m-rL))]R_{N}(m)\\ &=[\sum_{r=-\infty}^{\infty}r_{xy}(n-r N)] R_{N}(m) \end{aligned} rˉxy​(m)​=n=0∑N1​−1​x(n)y((n−m))N​RN​(m)=[n=0∑N1​−1​x(n)r=−∞∑∞​y(n−m+rL)]RN​(m)=[r=−∞∑∞​n=0∑n=N1​−1​x(n)y(n−(m−rL))]RN​(m)=[r=−∞∑∞​rxy​(n−rN)]RN​(m)​
其中，rxy(n)=x(n)∗y(−n)r_{xy}(n)=x(n)*y(-n)rxy​(n)=x(n)∗y(−n) 是线性相关。

% File: snrmse.m
% Software given here is to accompany the textbook: W.H. Tranter, 
% K.S. Shanmugan, T.S. Rappaport, and K.S. Kosbar, Principles of 
% Communication Systems Simulation with Wireless Applications, 
% Prentice Hall PTR, 2004.
%
function [gain,delay,px,py,rxy,rho,snrdb] = snrmse(x,y)
ln = length(x);                 % Set length of the reference (x) vector
fx = fft(x,ln);                 % FFT the reference (x) vector
fy = fft(y,ln);                 % FFT the measurement (y) vector
fxconj = conj(fx);              % Conjugate the FFT of the reference vector
sxy = fy .* fxconj;             % Determine the cross PSD 
rxy = ifft(sxy,ln);             % Determine the cross correlation function
rxy = real(rxy)/ln;             % Take the real part and scale
px = x*x'/ln;                   % Determine power in reference vector
py = y*y'/ln;                   % Determine power in measurement vector
[rxymax,j] = max(rxy);          % Find the max of the crosscorrelation
gain = rxymax/px;               % Here's the gain
delay = j-1;                    % Here's the delay
rxy2 = rxymax*rxymax;           % Square rxymax for later use
rho = rxymax/sqrt(px*py);       % Here's the correlation coefficient
snr = rxy2/(px*py-rxy2);        % Here's the snr
snrdb = 10*log10(snr);          % Here's the snr in db
% End of script file.

这个MATLAB代码是很有问题的，我来解释一下。x 是输入参考信号 x(t)x(t)x(t) ，y(t)y(t)y(t) 为观测信号。

正常来说我们想要用 FFT 做线性相关必须要先补零，但是这里没有补零，那么我们直接用 ln = length(x); 的信号会得到什么？

没错，我们得到的实际上是循环卷积。

那么为什么结果依然还是基本上没有问题的呢？如下图

其实问题出在 z(t)=Ax(t−τ)z(t)=A x(t-\tau)z(t)=Ax(t−τ) 上，这里 τ\tauτ 其实是非常小的，我们从下文可以知道 τ\tauτ 是 64，其实是非常小的，相较于信号的长度来看。我们来看我们直接得到的信号是什么。

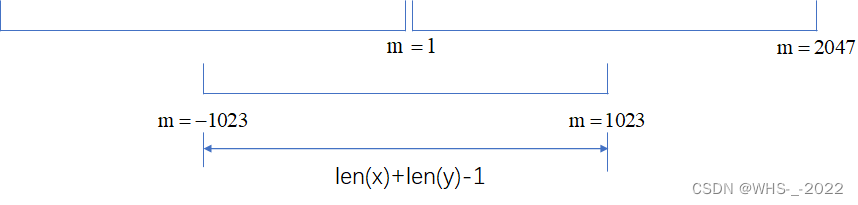
可以看到，m=−64m=-64m=−64 的时候会取到相关系数的最大值，此时 mmm 较大值处的影响是比较小的，可以近似的认为这就是 rxyr_{xy}rxy​ 的值。

此外还有一点，这里取实部是没有必要的，因为实函数的相关函数必然也是个实数。

%在输入x和y都是实数的情况下,相关函数rxy必定是实数，这里是没有必要的
rxy = ifft(sxy,ln);             % Determine the cross correlation function
rxy = real(rxy)/ln;             % Take the real part and scale
% isreal(rxy)
% ans =
% 
%   logical
% 
%    1
%

二、附录

rˉxy(m)=∑n=0N1−1x(n)y((n−m))NRN(m)=[∑n=0N1−1x(n)∑r=−∞∞y(n−m+rL)]RN(m)=[∑r=−∞∞∑n=0n=N1−1x(n)y(n−(m−rL))]RN(m)=[∑r=−∞∞rxy(n−rN)]RN(m)\begin{aligned} \bar{r}_{x y}(m) & =\sum_{n=0}^{N_1-1} x(n) y((n-m))_{N} R_{N}(m) \\ &=[\sum_{n=0}^{N_1-1} x(n) \sum_{r=-\infty}^{\infty}y(n-m+rL) ]R_{N}(m)\\ &=[\sum_{r=-\infty}^{\infty} \sum_{n=0}^{n=N_1-1}x(n)y(n-(m-rL))]R_{N}(m)\\ &=[\sum_{r=-\infty}^{\infty}r_{xy}(n-r N)] R_{N}(m) \end{aligned} rˉxy​(m)​=n=0∑N1​−1​x(n)y((n−m))N​RN​(m)=[n=0∑N1​−1​x(n)r=−∞∑∞​y(n−m+rL)]RN​(m)=[r=−∞∑∞​n=0∑n=N1​−1​x(n)y(n−(m−rL))]RN​(m)=[r=−∞∑∞​rxy​(n−rN)]RN​(m)​

为了验算圆周相关是线性相关的平移，我花了很多时间来验证这个公式，代码分享给大家。

% 验算圆周相关
L=4;x=[1,1,5,7];y=[2,2,3,7];
% 直接用卷积的方法求相关函数
corr=xcorr(x,y)%用FFT的方法求相关函数
lnx = length(x);                
lny = length(y); 
fx = fft(x,lnx+lny-1);                 % FFT the reference (x) vector
fy = fft(y,lny+lnx-1);                 % FFT the measurement (y) vector
fyconj = conj(fy);             
sxy = fx .* fyconj;             
rxy = ifft(sxy,lnx+lny-1);             %计算出来的恰好以 lnx+lny-1 为长度的圆周相关%需要将FFT得到的相关函数向右位移Ny-1个单位,得到的rxy第一个值的下标是和线性相关一致
rxy=circshift(rxy,lny-1)
rxy_1=[rxy,zeros(1,L)]%补零,为平移相加做准备
%接下来求圆周相关结果rxy_2=[zeros(1,L),rxy(1:end)]%向右移动
rxy_3=rxy_1+rxy_2
RXY=rxy_3(lny:1:lny+L-1)%圆周相关取主值%%%接下来我们直接以圆周相关周期L，用FFT计算圆周相关ln = length(L);                 % Set length of the reference (x) vector
fx = fft(x,L);                 % FFT the reference (x) vector
fy = fft(y,L);                 % FFT the measurement (y) vector
fyconj = conj(fy);              % Conjugate the FFT of the reference vector
sxy = fx .* fyconj;             % Determine the cross PSD 
rxy2 = ifft(sxy,L)             % Determine the cross correlation function