线性动态规划问题
创始人
2025-05-31 14:17:29
文章目录
- 1. 三角形中最小路径之和
- 2. 最长递增子序列
- 3. 最长公共子序列
1. 三角形中最小路径之和
给定一个三角形 triangle ,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
示例:

分析:
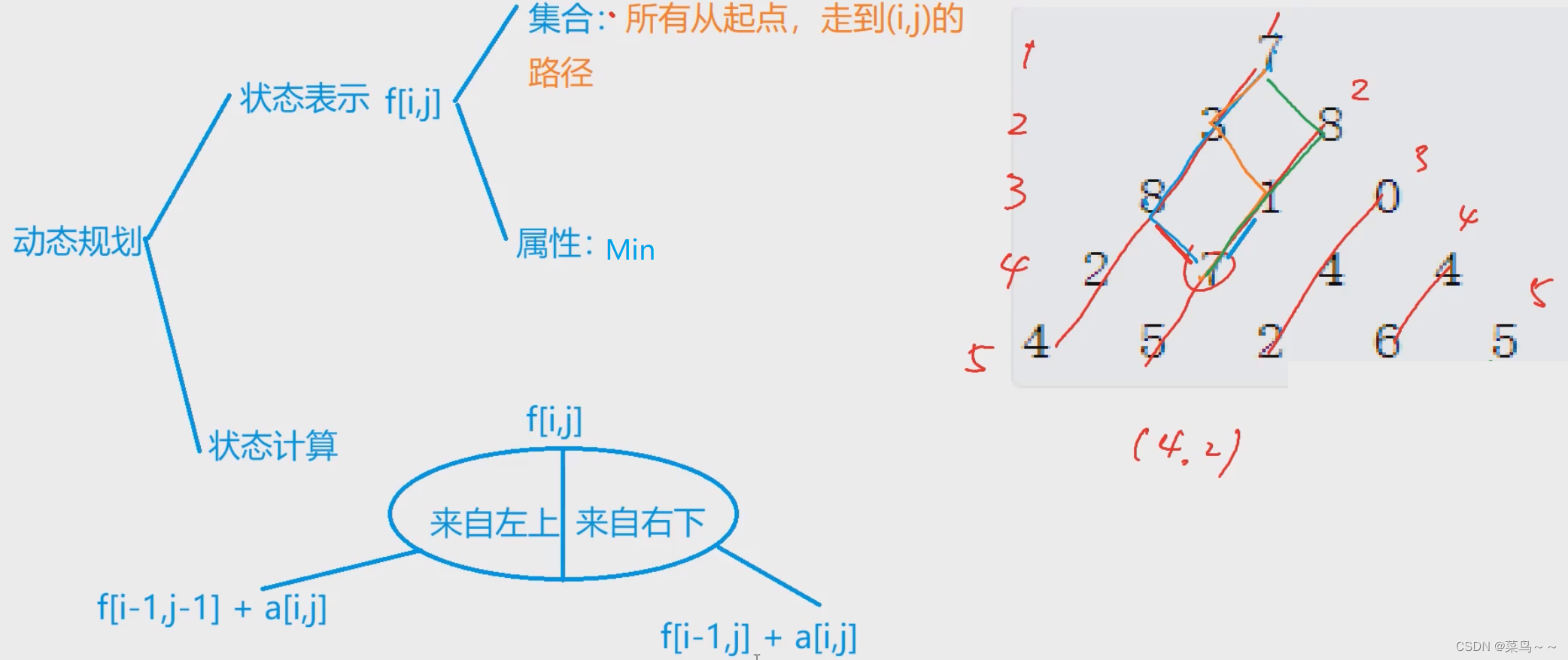
一般涉及到i-1的下标,我们i的取值从1开始。
动态规划问题的时间复杂度一般为:状态数量*转移计算量。
- 二维数组:自顶向下
class Solution {
public:int minimumTotal(vector>& triangle) {int dp[201][201];int n = triangle.size();//不能使用int dp[201][201] = {INT_MAX},因为这个仅仅是把dp[0][0] = INT_MAX,其余还是0for (int i = 0; i < 201; ++i) {for (int j = 0; j < 201; ++j) {dp[i][j] = INT_MAX;}}dp[0][0] = triangle[0][0];int minpath = INT_MAX;for(int i = 1; i < n; ++i){for(int j = 0; j <= i; ++j){if(j > 0) dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j]) + triangle[i][j];else dp[i][j] = dp[i - 1][j] + triangle[i][j];}}for(int i = 0; i < n; ++i){minpath = min(minpath, dp[n - 1][i]);}return minpath;}
};
时间复杂度:O(n^2), 空间复杂度:O(n^2)
- 一维数组:自底向上
class Solution {
public:int minimumTotal(vector>& triangle){int dp[201];int n = triangle.size() - 1;for(int i = 0; i <= n; ++i){dp[i] = triangle[n][i];}for(int i = n - 1; i >= 0; --i){for(int j = 0; j <= i; ++j){dp[j] = min(dp[j] + triangle[i][j], dp[j + 1] + triangle[i][j]);}}return dp[0];}
};
时间复杂度:O(n^2),空间复杂度:O(n)
2. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
分析

class Solution {
public:int lengthOfLIS(vector& nums) {int dp[2501];for(int i = 0; i < nums.size(); ++i){dp[i] = 1;for(int j = 0; j < i; ++j){if(nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);}}int result = 0;for(int i = 0; i < nums.size(); ++i) result = max(result, dp[i]);return result;}
};
如何保存最长递增子序列
int lengthOfLIS(vector& nums) {int dp[2501];int g[2501]; //记录最长子序列for (int i = 0; i < nums.size(); ++i) {dp[i] = 1;g[i] = 0;for (int j = 0; j < i; ++j) {if (nums[i] > nums[j]) {if (dp[i] < dp[j] + 1) {dp[i] = dp[j] + 1;//记录dp[i]从哪个状态转移过来的g[i] = j;}}}}int result = 0;int k = 0;for (int i = 0; i < nums.size(); ++i) {if (dp[k] < dp[i]) {k = i;}}result = dp[k];//倒着输出,如果需要正着输出只需要逆序就可以for (int i = 0; i < result; ++i) {cout << nums[k] << " ";k = g[k];}cout << endl;return result;
}
int main()
{vector num = {0,1,0,3,2,3};cout< 
3. 最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
分析:主要就是两大情况: text1[i - 1] 与 text2[j - 1]相同,text1[i - 1] 与 text2[j - 1]不相同
- 如果
text1[i - 1] 与 text2[j - 1]相同,那么找到了一个公共元素,所以dp[i][j] = dp[i - 1][j - 1] + 1; - 如果
text1[i - 1] 与 text2[j - 1]不相同,那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列,取最大的。即:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
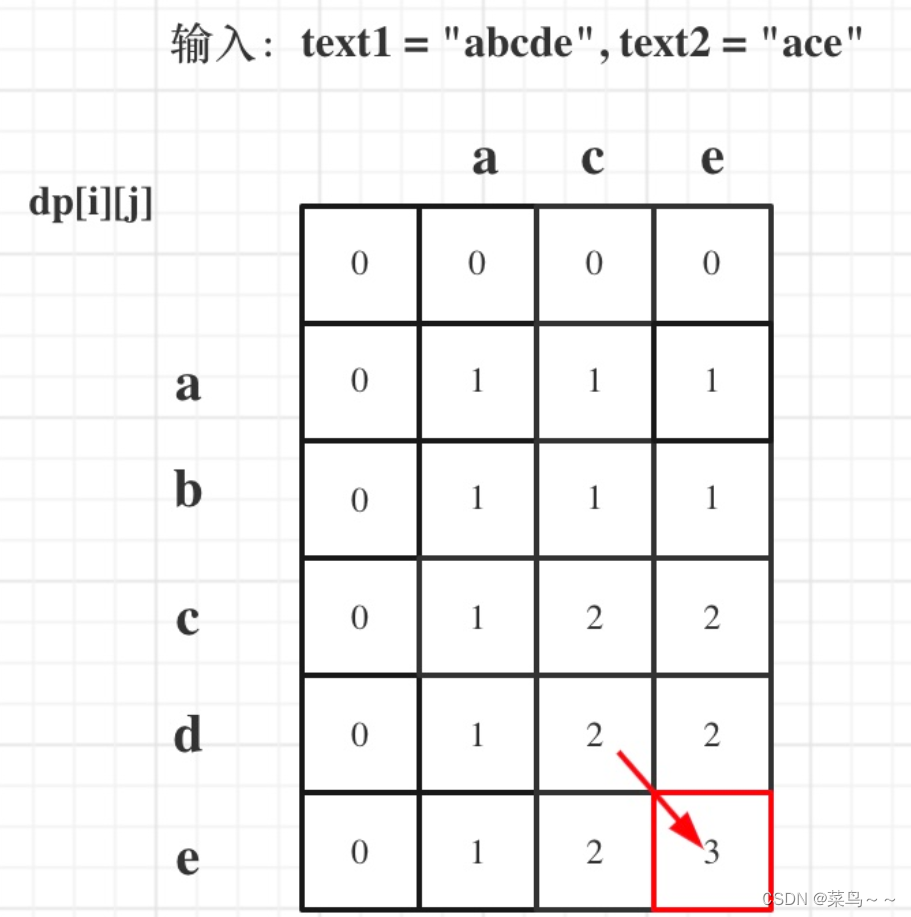
class Solution {
public:/*//递归实现会超时int longestCommonSubsequence(string text1,int n,string text2,int m){if(n < 0 || m < 0){return 0;}if(dp[n][m] >= 0){return dp[n][m];}if(text1[n] == text2[m]){dp[n][m] = 1 + longestCommonSubsequence(text1,n-1,text2,m-1);}else{int l1 = longestCommonSubsequence(text1,n-1,text2,m);int l2 = longestCommonSubsequence(text1,n,text2,m-1);dp[n][m] = max(l1,l2);}return dp[n][m];}int longestCommonSubsequence(string text1, string text2) {dp.resize(text1.size(),vector(text2.size(),-1));return longestCommonSubsequence(text1,text1.size()-1,text2,text2.size()-1);}
private:vector> dp;*///动态规划int longestCommonSubsequence(string text1, string text2) {int i = text1.size();int j = text2.size();vector> dp(i+1,vector(j+1,0));for(int n = 1;n <= i;n++){for(int m = 1;m <= j;m++){if(text1[n-1] == text2[m-1]){dp[n][m] = 1 + dp[n-1][m-1];}else{dp[n][m] = max(dp[n-1][m],dp[n][m-1]);}}}return dp[i][j];}
};
相关内容
热门资讯
北京的名胜古迹 北京最著名的景...
北京从元代开始,逐渐走上帝国首都的道路,先是成为大辽朝五大首都之一的南京城,随着金灭辽,金代从海陵王...
苗族的传统节日 贵州苗族节日有...
【岜沙苗族芦笙节】岜沙,苗语叫“分送”,距从江县城7.5公里,是世界上最崇拜树木并以树为神的枪手部落...
世界上最漂亮的人 世界上最漂亮...
此前在某网上,选出了全球265万颜值姣好的女性。从这些数量庞大的女性群体中,人们投票选出了心目中最美...
长白山自助游攻略 吉林长白山游...
昨天介绍了西坡的景点详细请看链接:一个人的旅行,据说能看到长白山天池全凭运气,您的运气如何?今日介绍...
