Python数据结构与算法（p1-p6）
学习材料
清华大学博士讲解Python数据结构与算法 B站：https://www.bilibili.com/video/BV1uA411N7c5/?spm_id_from=333.1007.top_right_bar_window_default_collection.content.click&vd_source=0280f569cc8b52d702c3f57798aefe5c
《Python数据结构与算法分析》，作者：布拉德利·米勒，戴维·拉努姆
一、算法的基础
1、什么是算法
算法（Algorithm）是一个计算过程，解决问题的方法。
“程序 = 数据结构+算法”
算法是有输入和输出的。
2、时间复杂度
时间复杂度，用来评估算法运行的效率，用O( )表示。O表示估计/大约，()的内容表示单位。
举例：
(1)打印、运算等程序的基本操作，时间复杂度为O(1)。
print("Hello World") （2）n次循环的代码，时间复杂度为O(n)。
for i in range(n):print("Hello World")(3) 循环嵌套，for循环内还有一个for循环，时间复杂度为O(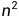
)。
for i in range(n):for j in range(n):print("Hello World")（4）三次循环嵌套，for循环中嵌套了两个for循环，时间复杂度为O(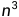
)。
for i in range(n):for j in range(n):for k in range(n):print("Hello World")(5)问题规模减半的循环，时间复杂度为O(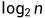
)，简称为O(logn)，对数。
while n>1:print(n)n = n // 2#假如n = 64
#输出结果为：
64
32
16
8
4
2小结
（1）时间复杂度是用来估计算法运行时间的一个式子（单位）。
（2）一般来说，时间复杂度高的算法比复杂度低的算法运行的慢。
（3）常见的时间复杂度（按效率排）：
O(1)
(4)复杂问题的时间复杂度
O(n!), O(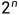
),O(
)
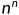如何简单快速的判断时间复杂度？
（1）快速判断算法复杂度（适用于大多数简单情况）：
确定问题规模n；
循环减半过程 ——>logn；
K层关于n的循环 ——>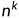
。
（2）复杂情况：根据算法执行过程判断。
3、空间复杂度
空间复杂度：用来评估算法内存占用大小的式子。
空间复杂度的表达式与时间复杂度完全一样：
算法使用了几个变量：O(1);
算法使用了长度为n的一维列表：O(n);
可以理解为：
for i in range(n):print("Hello World")算法使用了m行n列的二维列表：O(mn)。
可以理解为：
for i in range(n):for j in range(m):print("Hello World")“空间换时间”
时间比空间更重要，所以大部分算法都以降低时间复杂度为目标。
4、递归
（1）递归有两个特点：
a.调用自身
b.有结束条件
（2）递归示例
1）print在函数之前运行
def func3(x):if x > 0:print(x)func3(x-1)递归运行逻辑：当x=3时
[func(3)---->print（3）]----->[func3(2)---->print(2)]---->[func3(1)---->print(1)]---->[func3(0)]
输出结果：3 2 1
2）print在函数之后
def func4(x):if x > 0:func4(x-1)print(x)递归运行逻辑：当x=3时
func4(3)---->{func4(2)---->[func4(1)---->(func4(0))---->print(1)]---->print(2)}---->print(3)
从内往外print
输出结果：1 2 3
5、汉诺塔问题-递归
（1）问题
有三根柱子，其中一根柱子上从下往上按大小顺序摞着n个圆盘，要求将圆盘从下面开始按大小顺序重新摆放在另一根柱子上，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。
（2）解题思路：
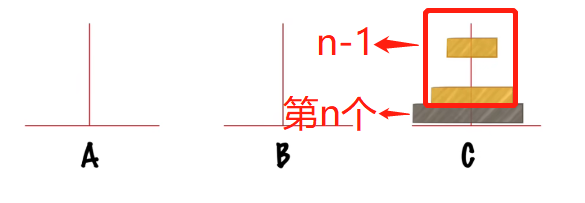
当n个盘子时：将上面的n-1个圆盘看成一体，圆盘完成转移需要经过以下三步，
step1：把n-1个小圆盘从A经过C移动到B；
step2：把第n个圆盘从A移动C；
step3：把n-1个小圆盘从B经过A移动到C。
（3）代码如下：
#汉诺塔-递归def hanoi(n,a,b,c): #第n块，a，b，c三根柱子if n>0:hanoi(n-1,a,c,b) #n-1块圆盘从a位置经过c移动到bprint(f"moving from {a} from {c}") #第n块圆盘从a移到chanoi(n-1,b,a,c) #n-1块圆盘从b位置经过a位置移到到c位置hanoi(3,"A","B","C")#输出结果
moving from a from c
moving from a from b
moving from c from b
moving from a from c
moving from b from a
moving from b from c
moving from a from c（4）汉诺塔移动次数递推式：
根据解题思路，每移动一次记1，可得递推式：
h(x) = 2h(x-1)+1.
解析：
step1：把n-1个小圆盘从A经过C移动到B------->移动h（x-1）次；
step2：把第n个圆盘从A移动C------->移动1次；
step3：把n-1个小圆盘从B经过A移动到C--------->移动h（x-1）次。
（5）汉诺塔问题移动次数求解代码
1）根据移动步骤，python代码如下：
class num():def __init__(self):self.x = 0 #x为每次运算def hanoi(self,n,a,b,c): #第n块，a，b，c三根柱子if n>0:self.hanoi(n-1,a,c,b) #n-1块圆盘从a位置经过c移动到bprint(f"moving from {a} from {c}") #第n块圆盘从a移到cself.x += 1 #移动一次计数self.hanoi(n-1,b,a,c) #n-1块圆盘从b位置经过a位置移到到c位置len_n =num() #类实例化
len_n.hanoi(3,"a","b","c") #移动策略
print(len_n.x) #运行次数#输出结果
moving from a from c
moving from a from b
moving from c from b
moving from a from c
moving from b from a
moving from b from c
moving from a from c
72）根据递推式，计算n个圆盘的移动次数，代码如下：
#汉诺塔递推式h(n) = 2h(n-1)+1
def han(n): #n为大于0的整数if n == 0:return 0else:return (han(n-1) * 2 + 1) print(han(3))#输出结果
7(6)拓展练习——斐波那契数列
1）问题：
大家都知道斐波那契数列，现在要求输入一个正整数 n ，请你输出斐波那契数列的第 n 项。
斐波那契数列是一个满足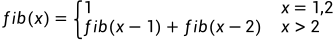
的数列。
2）求解代码-递归
def Fibonacci(n) :# write code hereif n < 2: #当n=0和n=1时，返回本身return nelse:return (Fibonacci(n - 1) + Fibonacci(n - 2)) #n>2时，计算方式为f(n-1)+f(n-2)3)时间复杂度和空间复杂度
时间复杂度在最坏情况下为 O(2^n)，因为每个斐波那契数都需要在前面的两个斐波那契数的基础上计算。空间复杂度也是 O(n)，因为在最坏情况下，需要存储 n 个斐波那契数。