学Python的第十天---小蓝(1)
- 一、字符排序
- 写法一:
- 写法二:
- 二、付账问题(贪心)
- 写法一:自己的写法
- 写法二:
- 时间复杂度
- 三、第几个幸运数字(枚举---排列性枚举)
- 组合型枚举
- 排列型枚举
- 也可以用函数permutations()
- 四、排列序数(permutations)
- 五、火星人
- 六、回文判定(双指针)
- 写法一:双指针
- 写法二:切片
- 七、美丽区间(尺取法)
- 八、约数个数
- 写法一:暴力法
- 写法二:剪枝
- 九、特殊时间(模拟)
- 十、递归和递推
- 递推
- 斐波那契数列
- 低效代码:
- 记忆化
- 数字三角形
一、字符排序
将“WHERETHEREISAWILLTHEREISAWAY”排序
输出为“AAAEEEEEEHHHIIILLRRRSSTTWWWY”
写法一:
s="WHERETHEREISAWILLTHEREISAWAY"
s=sorted(s)
print(*s,sep='')
写法二:
s = "WHERETHEREISAWILLTHEREISAWAY"
s = ''.join(sorted(s))
print(s)二、付账问题(贪心)


标准差
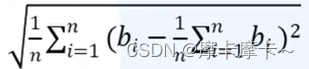
写法一:自己的写法
n, s = map(int, input().split())
a = list(map(int, input().split()))
a.sort()
avg=s/n
res = 0
for i in range(n):if a[i] * (n - i) >= s:#说明她钱够res+=(s/(n-i)-avg)**2*(n-i)breakelse:res+=(a[i]-avg)**2s-=a[i]
res=(res/n)**0.5
print("{:.4f}".format(res))
写法二:
from math import *
n,s=map(int,input().split())
a=list(map(int,input().split()))
a.sort()
avg=s/n
sum=0
for i in range(n):if a[i]*(n-i)时间复杂度
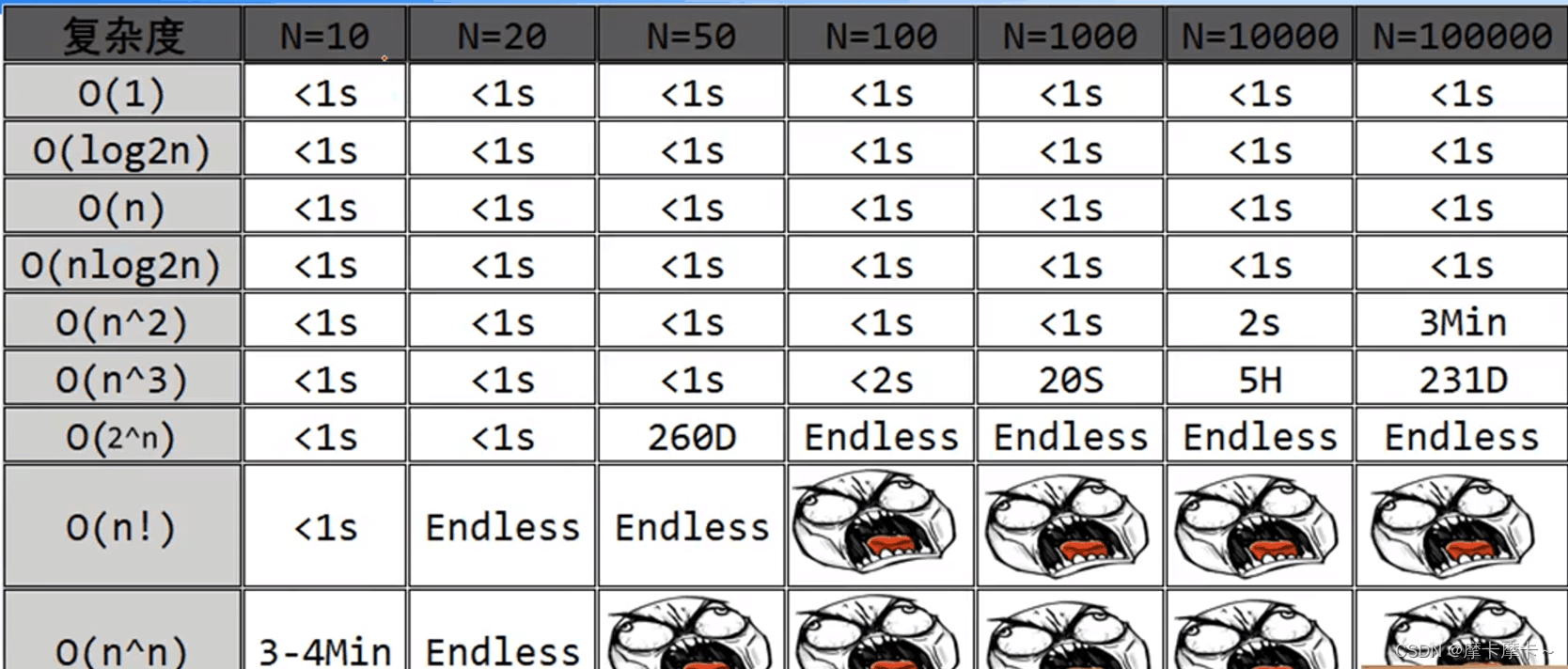
时间复杂度不超过10^9,就可能会过
三、第几个幸运数字(枚举—排列性枚举)

n=59084709587505
cnt=0
for i in range(50):#3^50一定超过了nfor j in range(50):for z in range(50):a=3**ib=5**jc=7**zif a*b*c<=n:cnt+=1
print(cnt-1)#幸运数字不包括1
组合型枚举
让你在n个中随机选出m个。Cnm(数学公式那个)
模板:
chosen=[]
n,m=0,0def calc(x):if len(chosen)>m:returnif len(chosen)+n-x+1排列型枚举
当组合型枚举的cnm的m变成n,就变成了排列型枚举
order=[0]*20
chosen=[0]*20
n=0
def calc(x):if x==n+1:for i in range(1,n+1):print(order[i],end=' ')print('')returnfor i in range(1,n+1):if (chosen[i]==1):continueorder[x]=ichosen[i]=1calc(x+1)chosen[i]=0order[x]=0
if __name__=='_main':n=int(input())calc(1)
也可以用函数permutations()

from itertools import *
s=['a','b','c']
for element in permutations(s,2):#这里的2表示想要几个数a=element[0]+element[1]#或者可以这样子写 a=''.join(element)print(a)
四、排列序数(permutations)

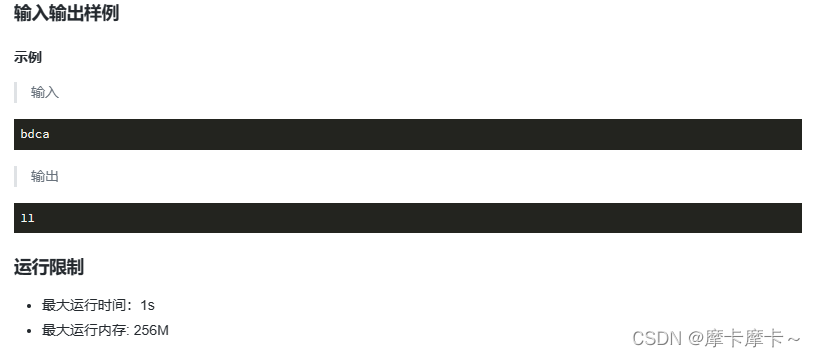
我一开始写错了,是因为我以为固定了输入的字符,abcd,结果并不固定,要掌握这个permutations函数。
permutations(iterable, r=None) 是 Python 标准库中 itertools 模块中的函数,用于返回可迭代对象的所有排列方式,即所有可能的序列。
iterable: 可迭代对象,例如字符串、列表、元组等
r: 需要选择元素的数量,默认为 None,表示选择全部元素
permutations() 生成一个迭代器,迭代器的元素是 iterable 中所有元素的排列组合,包含每一种排列方式。排列的顺序是按照字典序排列的,例如:permutations(‘ABCD’) 返回的迭代器按照 ‘ABCD’, ‘ABDC’, ‘ACBD’, … 的顺序排列。如果设置了 r,则只返回选定数量的排列。
from itertools import *
olds=input()
news=list(olds)
news.sort()
cnt=0
for element in permutations(news):a=''.join(element)if olds==a:print(cnt)breakcnt+=1
五、火星人

Python的permutations()这个函数是按照元素位置进行排列的输出的。
这段代码实现了一个求全排列中的下一个排列的算法。其基本思路是:从后往前找到第一个相邻升序对,即 nums[i] < nums[i+1],然后在 nums[i+1:] 中找到比 nums[i] 大的最小数,将它们交换,并将 nums[i+1:] 中的数逆序,得到下一个排列。
具体来说,对于一个长度为 n 的排列,第一次找到相邻升序对的时间复杂度为 O(n),而第二次交换和逆序的时间复杂度为 O(n-i),因此整个算法的时间复杂度为 O(n)。
在本例中,m 次操作都是单独地对 nums 进行操作,因此总时间复杂度为 O(mn)。
n=int(input())
m=int(input())
nums=list(map(int,input().split()))
def find_next(nums):for i in range(n-1,0,-1):if nums[i]>nums[i-1]:for j in range(n-1,i-1,-1):if nums[j]>nums[i-1]:nums[j],nums[i-1]=nums[i-1],nums[j]return nums[:i]+nums[:i-1:-1]
for i in range(m):nums=find_next(nums)
print(" ".join([str(i) for i in nums]))六、回文判定(双指针)

写法一:双指针
还有while…else的用法
s=input()
i=0
j=len(s)-1
if i==j:print("Y")
else:while s[i]==s[j]:i+=1j-=1if j写法二:切片
s=input()
ss=s[::-1]
if s==ss:print("Y")
else:print("N")
七、美丽区间(尺取法)

很直接的滑动窗口,求窗口内的区间和,满足大于S的最小长度。
i指针在前,j指针在后,计算两个指针之间的区间和,当i指针达到末尾时,结束计算。
计算复杂度为O(n)
n,s=map(int,input().split())
a=list(map(int,input().split()))
i,j,sum,ans=0,0,0,100000
while i八、约数个数

写法一:暴力法
n=1200000
res=0
for i in range(1,n+1):if n%i==0:res+=1
print(res)
写法二:剪枝
se = set()
for i in range(1,int(1200000**0.5)+1):if 1200000%i==0:se.add(i)se.add(1200000//i)
print(len(se))
九、特殊时间(模拟)

day_per_month=[0,31,28,31,30,31,30,31,31,30,31,30,31]
def check_D(D):month =D//100day=D%100if month <1 or month>12:return 0if day<1 or day>day_per_month[month]:return 0return 1def check_H(H):h=H//100m=H%100if h<0 or h>23:return 0if m<0 or m>59:return 0return 1
ans=0
for a in range(10):for b in range(10):if a==b:continueN_Y,N_D,N_H=4,0,0#年份都满足要求A=[a,a,a,a]for i in range(4):A[i]=bnumber=0for j in A:number=number*10+jN_D+=check_D(number)N_H+=check_H(number)A[i]=aans+=N_Y*N_D*N_H
print(ans)
十、递归和递推
递推


单次查询可以不进行存储,多次查询都要进行存储(记忆性搜索)。
斐波那契数列
低效代码:
cnt=0
def fib(n):global cntcnt+=1if n==1 or n==2:return 1return fib(n-1)+fib(n-2)print(fib(20))
print(cnt)

记忆化
data=[0 for i in range(25)]
cnt=0
def fib(n):global cntcnt+=1if data[n]!=0:#记忆化搜索,如果算了,就不用再算了,直接返回答案return data[n]if n==1 or n==2:data[n]=1return data[n]data[n]=fib(n-1)+fib(n-2)return data[n]print(fib(20))
print(cnt)
数字三角形


从后面往前面算,这样子的选择就会减少,这样子才可以推出最优的
在没有左右两边次数差不超过1的条件,代码可以这样子写!!!注意,这里是没有左右两边次数差的限制。
a=[[0]*101]*101
if __name__=='__main__':n=int(input())for i in range(1,n+1):a[i]=input().split()a[i]=list(map(int,a[i]))for i in range(n-1,0,-1):for j in range(0,i):if a[i+1][j]>=a[i+1][j+1]:a[i][j]+=a[i+1][j]else:a[i][j]+=a[i+1][j+1]
print(a[1][0])
该题目有向左边走和向右边走的次数不能超过1,故最后肯定是在中间
h = int(input()) # 输入数据
W = [list(map(int, input().split())) for i in range(h)]
# 循环遍历计算到每一行的和的最大值
for i in range(1, h):for j in range(0, i + 1):if j == 0: # 最左边元素只能由右上方得到W[i][j] += W[i - 1][j]elif j == i: # 最右边元素只能由左上方得到W[i][j] += W[i - 1][j - 1]else: # 其余元素由上方较大值得到W[i][j] += max(W[i - 1][j - 1: j + 1])
if h & 1: # 如果是奇数行,则返回最中间值print(W[-1][h // 2])
else: # 偶数行则返回中间较大值print(max(W[-1][h // 2 - 1], W[-1][h // 2]))
上一篇:Opentss代码测试
下一篇:<Linux>环境变量
