D - Bank (atcoder.jp)
(1)题目大意
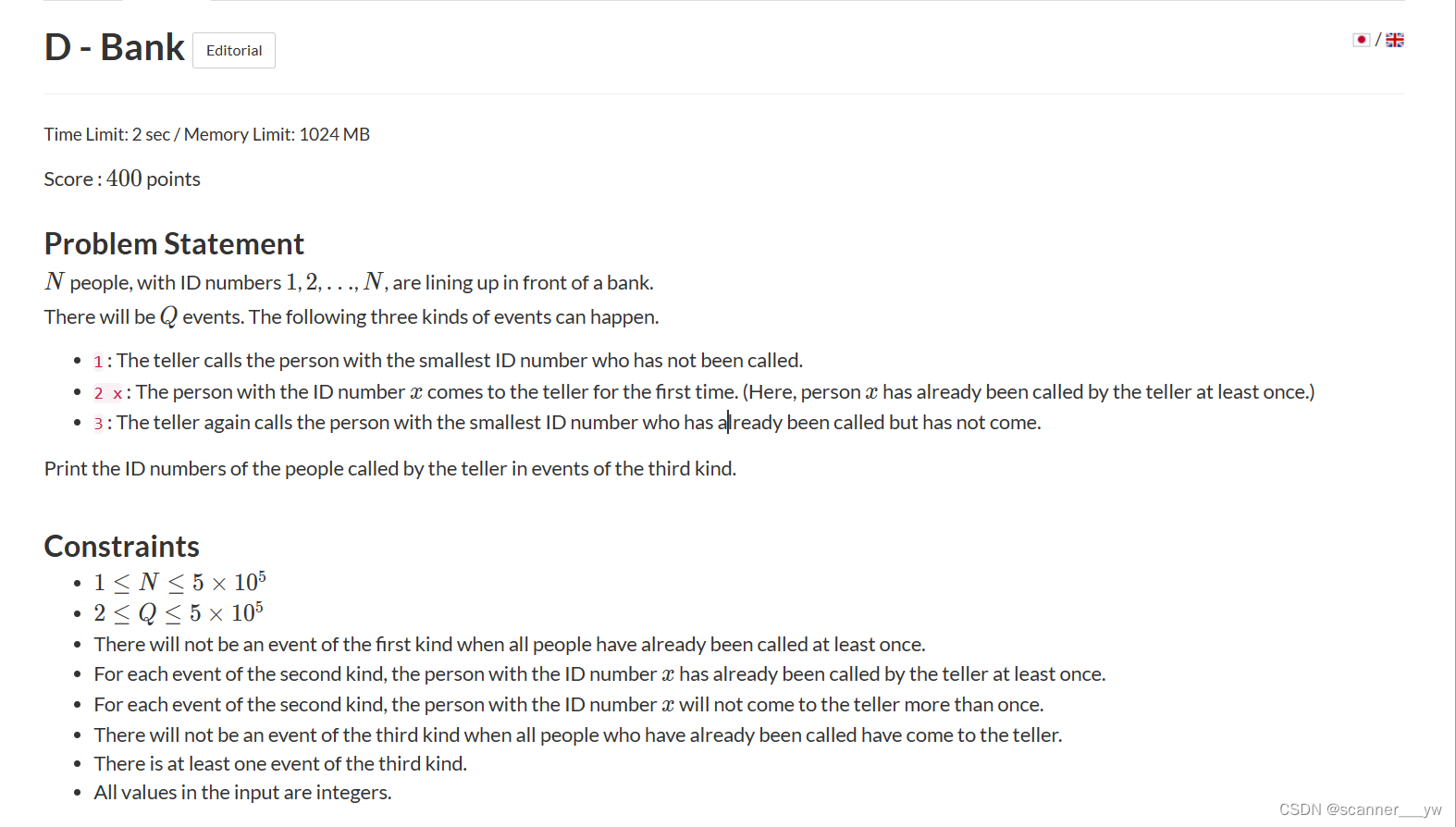
给你N个id,以及Q个询问,1表示用未被用到的最小的一个id,2表示x这个id现在被用到了,3表示再喊已经被喊的最小的那个人的id。
(2)解题思路
用两个set模拟即可。
(3)代码实现
#include
#include
E - 2xN Grid (atcoder.jp)
(1)题目大意
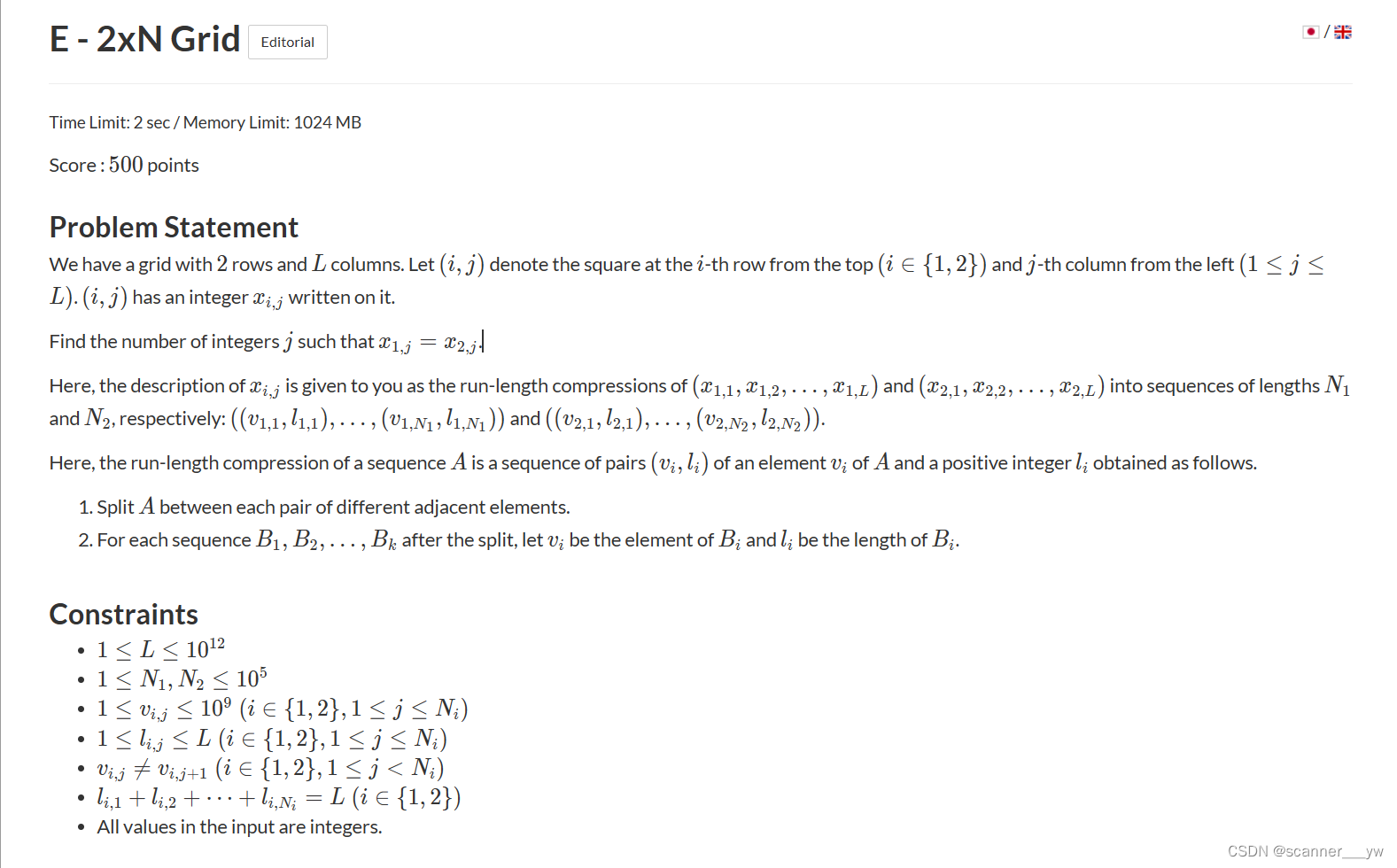
给你一个2*L的矩阵,第一行有N1个小段,每一段是一个数,第二行有N2个小段,每一段也是一个数,问你有多少对A[1][j] = A[2][j]
(2)解题思路
类似于区间合并的思想,使用双指针,若当上下指针区间元素一样,则算这个区间的交集是多少,然后根据上下指针的右边界的大小移动指针即可。
(3)代码实现
#include
#include
F - Sugar Water 2 (atcoder.jp)
(1)题目大意
两个人分别由N个瓶子和M个瓶子的糖水,设第一个人第i个瓶子由Ai克糖和Bi克水,第二个人第j个瓶子由Cj克糖和Dj克水,分别从两个人中取出一个瓶子,问你第k大糖分率是多少?
(2)解题思路
考虑k过大,因此考虑二分答案V
式子可以写为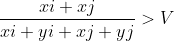 ,若满足这个式子有大于V的个数有K个,那么此答案符合要求,把除法变乘法
,若满足这个式子有大于V的个数有K个,那么此答案符合要求,把除法变乘法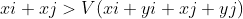 ,把i放一边j放一边变为
,把i放一边j放一边变为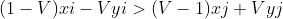 ,把AB数组处理成左边式子,把CD数组处理成右边式子,排个序双指针扫一下看有多少个满足条件即可。
,把AB数组处理成左边式子,把CD数组处理成右边式子,排个序双指针扫一下看有多少个满足条件即可。
(3)代码实现
#include
#include
G - Distance Queries on a Tree (atcoder.jp)
(1)题目大意
给你一颗树有N个节点,有两种操作,第一种操作是把第i条边的权值修改为w,第二个操作是询问u到v的路径和。

(2)解题思路
预处理出dfs序,因为树上操作不好直接修改,因此转换成区间问题,又因为是边权和,我们可以按照dfs序把边权转换为点权处理,按照拆点的思路把树上每一个点分成入点和出点,若修改了第i条边的权值,相当于修改了第i条边的入点的和,然后在这个出点+1的位置减去修改的即可,因此可以考虑树状数组进行单点修改和区间查询。
注意查询的时候我们是qry[1,in[u]] + qry[1,in[v]] - 2 *qry[1,lca(in[u],in[v]));查询的时候是直接查询第u节点之前的和和节点之前的和然后减去他们2倍lca的和,因为他们lca之前的全部都重复了,比如。
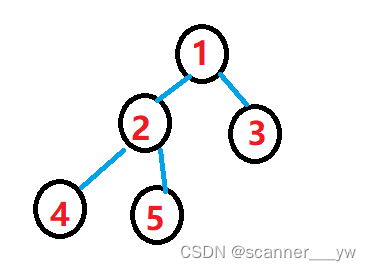
查询4和5的和,要减去2倍2之前的和。
(3)代码实现
#include
#include



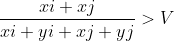 ,若满足这个式子有大于V的个数有K个,那么此答案符合要求,把除法变乘法
,若满足这个式子有大于V的个数有K个,那么此答案符合要求,把除法变乘法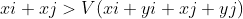 ,把i放一边j放一边变为
,把i放一边j放一边变为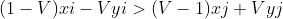 ,把AB数组处理成左边式子,把CD数组处理成右边式子,排个序双指针扫一下看有多少个满足条件即可。
,把AB数组处理成左边式子,把CD数组处理成右边式子,排个序双指针扫一下看有多少个满足条件即可。

