C++基础算法④——排序算法(插入、桶附完整代码)
创始人
2025-06-01 02:30:35

排序算法

1.插入排序

2.桶排序

1.插入排序

基本思想：将初始数据分为有序部分和无序部分；每一步将无序部分的第一个值插入到前面已经排好序的有序部分中，直到插完所有元素为止。
步骤如下：

  1. 每次从无序部分中取出第一个值，然后，与有序部分中的值从后向前依次比较；
  2. 有序部分比较：当前大于后就交换值；
  3. 重复①②步骤；直到不再交换，就结束循环！
  4. 最后输出循环结果。

假如有[5,2,3,9,4,7] 6个元素值，有序部分为[2,3,5,9]，无序部分为[4,7]；接下来要把无序部分的“4”元素插入到有序部分，来展示一下插入排序的运行过程。

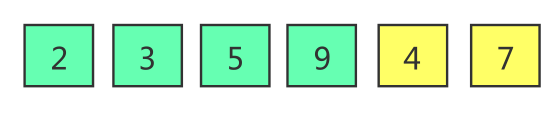
在这里插入图片描述

  1. 其中，浅绿色代表有序部分，黄色代表无序部分。
  2. 在无序部分中挑出要插入到有序部分中的元素。

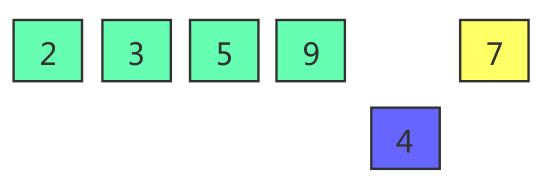
在这里插入图片描述

  1. 将插入的元素与左边最近的有序部分的元素进行比较。由于4 < 9，所以9向后移，4向前移。
    •  在这里插入图片描述
  2.  继续与左边最近的有序部分的元素进行比较。由于4 < 5，所以5向后移，4继续向前移。
    1. 在这里插入图片描述
  3. 继续将4与3比较。由于4 > 3，所以不再向前比较，插入到当前位置。此时有序部分，由[2,3,5,9] 变成 [2,3,4,5,9]。
    1. 在这里插入图片描述
//3.插入排序 
#include
using namespace std;
int a[1000],n;
int main(){cin>>n;for(int i=0;i>a[i];}for(int i=1;i=0;j--){if(a[j+1]前数，那循环结束了。 break;} }}for(int i=0;i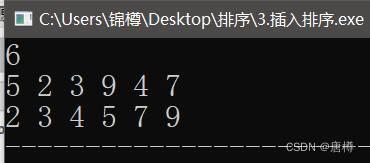

  1. 稳定性：在使用插入排序时，元素从无序部分移动到有序部分时，必须是不相等(大于或小于)时才会移动，相等时不处理，所以直接插入排序是稳定的。

  2. 时间复杂度：选择排序的时间复杂度为O(n^{2})。

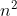  3. 适用场景：待排序序列的元素个数不多(<=50)，且元素基本有序。

2.桶排序

基本思想：将待排序的数值k，装入第k个桶，桶号就是待排序的数值，顺序输出各桶的值，得到有序的序列。

例如有 [5,4,9,4]，把数值依次装入桶a； 那可以看出 a[4] = 2，a[5] = 1，a[9] = 1；

那输出时候，按照顺序输出有桶号 4 4 5 9；
步骤：

  1. 先创建b桶数组并初始化值为0。
  2. 把k值装入第k个桶 b[k]++，对输入的同一个桶号，就累加。
  3. k是输入的桶号，也可以用a[i]表示，b[a[i]]++ 。
  4. 当有桶号数量 b[i]!=0 ，代表第i个桶是有值的，就输出桶号；
  5. 输出后就少了一个值要减掉，即 b[i]--。

编程对1万以内的数进行排序：

#include
using namespace std;
int a[100000],b[100000],n;
int main(){cin>>n; for(int i=1; i<=n; i++){cin >> a[i]; //输入桶号b[a[i]]++; // 统计桶号数量1 }for(int i=1; i<=10000; i++){while(b[i]!=0){ //当有桶号 cout<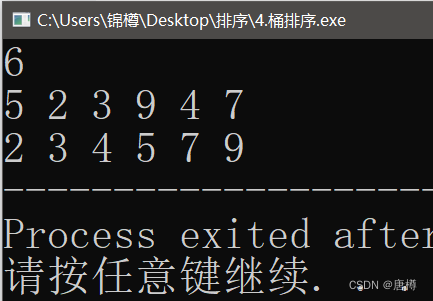

  1. 时间复杂度：选择排序的时间复杂度为O(n)。
  2. 适用场景：桶排序适用于数据量一般的排序场景。
词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：nginx快速入门.跟学B站nginx一小时精讲课程笔记

下一篇：【找工作】-- 大数据工程师找工作的正确姿势

相关内容

热门资讯

【实验报告】实验一 图像的... 实验目的熟悉Matlab图像运算的基础——矩阵运算；熟悉图像矩阵的显示方法࿰...
MATLAB | 全网最详细网... 一篇超超超长，超超超全面网络图绘制教程，本篇基本能讲清楚所有绘制要点&#...
大模型落地比趋势更重要，NLP... 全球很多人都开始相信，以ChatGPT为代表的大模型，将带来一场NLP领...
Linux学习之端口、网络协议... 端口：设备与外界通讯交流的出口 网络协议： 　　网络协议是指计算机通信网...
kuernetes 资源对象分... 文章目录1. pod 状态1.1 容器启动错误类型1.2 ImagePullBackOff 错误1....
STM32实战项目-数码管 程序实现功能： 1、上电后，数码管间隔50ms计数； 2、...
TM1638和TM1639差异... TM1638和TM1639差异说明 ✨本文不涉及具体的单片机代码驱动内容，值针对芯...
Qt+MySql开发笔记：Qt... 若该文为原创文章，转载请注明原文出处 本文章博客地址：https://h...
Java内存模型中的happe... 第29讲 | Java内存模型中的happen-before是什么？ Java 语言...
《扬帆优配》算力概念股大爆发，... 3月22日，9股封单金额超亿元，工业富联、鸿博股份、鹏鼎控股分别为3.0...
CF1763D Valid B... CF1763D Valid Bitonic Permutations 题目大意 拱形排列࿰...
SQL语法 DDL、DML、D... 文章目录1 SQL通用语法2 SQL分类3 DDL 数据定义语言3.1 数据库操作3.2 表操作3....
文心一言 VS ChatGPT... 3月16号，百度正式发布了『文心一言』，这是国内公司第一次发布类Chat...
CentOS8提高篇5：磁盘分...        首先需要在虚拟机中模拟添加一块新的硬盘设备，然后进行分区、格式化、挂载等...
Linux防火墙——SNAT、... 目录 NAT 一、SNAT策略及作用 1、概述 SNAT应用环境 SNAT原理 SNAT转换前提条...
部署+使用集群的算力跑CPU密... 我先在开头做一个总结，表达我最终要做的事情和最终环境是如何的，然后我会一...
Uploadifive 批量文... Uploadifive 批量文件上传_uploadifive 多个上传按钮_asing1elife的...
C++入门语法基础 文章目录：1. 什么是C++2. 命名空间2.1 域的概念2.2 命名...
2023年全国DAMA-CDG... DAMA认证为数据管理专业人士提供职业目标晋升规划，彰显了职业发展里程碑及发展阶梯定义...
php实现助记词转TRX，ET... TRX助记词转地址网上都是Java，js或其他语言开发的示例，一个简单的...
【分割数据集操作集锦】毕设记录 1. 按要求将CSV文件转成json文件 有时候一些网络模型的源码会有data.json这样的文件里...
Postman接口测试之断言 如果你看文字部分还是不太理解的话，可以看看这个视频，详细介绍postma...
前端学习第三阶段-第4章 jQ... 4-1 jQuery介绍及常用API导读 01-jQuery入门导读 02-JavaScri...
4、linux初级——Linu... 目录 一、用CRT连接开发板 1、安装CRT调试工具 2、连接开发板 3、开机后ctrl+c...
Urban Radiance ... Urban Radiance Fields:城市辐射场 摘要：这项工作的目标是根据扫描...
天干地支（Java） 题目描述 古代中国使用天干地支来记录当前的年份。 天干一共有十个，分别为：...
SpringBoot雪花ID长... Long类型精度丢失 最近项目中使用雪花ID作为主键，雪花ID是19位Long类型数...
对JSP文件的理解 JSP是java程序。（JSP本质还是一个Servlet） JSP是&#...
【03173】2021年4月高... 一、单向填空题1、大量应用软件开发工具，开始于A、20世纪70年代B、20世纪 80年...
LeetCode5.最长回文子... 目录题目链接题目分析解题思路暴力中心向两边拓展搜索 题目链接 链接 题目分析 简单来说࿰...