【蓝桥杯】 C++ 数字三角形 动态规划 ⭐⭐
创始人
2025-06-01 05:28:54

文章目录

    • 题目描述
      • 输入描述
      • 输出描述
    • 实现代码
    • 解题思路
    • 注意点
    • 知识点

题目描述

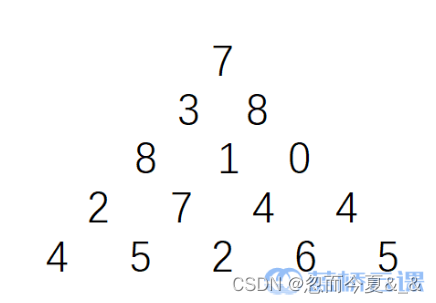
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和（路径上的每一步只可沿左斜线向下或右斜线向下走）。
在这里插入图片描述

输入描述

输入的第一行包含一个整数 N (1≤N≤100)，表示三角形的行数。下面的 N 行给出数字三角形。数字三角形上的数都是 0 至 99 之间的整数。

输出描述

输出一个整数，表示答案。

实现代码

#include
using namespace std;#define N 101int main()
{int n;cin>>n;int tri[N][N]={0};  // 存输入的三角形int dp[N][N]={0};   // 存动态规划算出来的数，到达每一个点最大的和for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){cin>>tri[i][j];}}// 要算 dp[i][j] ，就得知道 tri[i][j]和 dp[i-1][j] 和 dp[i-1][j-1] 中哪个最大for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+tri[i][j];}}int ans=dp[n][1];for(int i=1;i<=n;i++){if(dp[n][i]>ans){ans=dp[n][i];}}cout<

解题思路

这个题是动态规划的题目，首先根据题意发现这个和递归很像，通过子问题堆叠可以推出要求解的问题，同时动态规划通常用于最优解问题，解决这个问题比较方便。

  1. 把数字三角形存入二维数组，待后续取用。
  2. 把三角形变成直角三角形，如下图，可以发现要求第三行的 “1” 的最大ans，就需要知道第二行 “3” 和 “8” 的最大 ans，取较大的 ans，因此可得到达每一个点的 dp[ i ] [ j ] = dp[ i-1 ] [ j-1 ] + dp[ i-1 ] [ j ] + tri[ i ] [ j ]，
  3. 最后比较最后一行的每个数的ans，取最大即可得到答案。
    在这里插入图片描述

注意点

  • 注意 tri 和 dp 要开101个，不知道为什么，如果开 n+1 个的话，结果就不对……
  • 注意 dp[ i ][ j ] 的算法，加完上面最大的ans之后，还需要加 tri[ i ] [ j ] 的值。

知识点

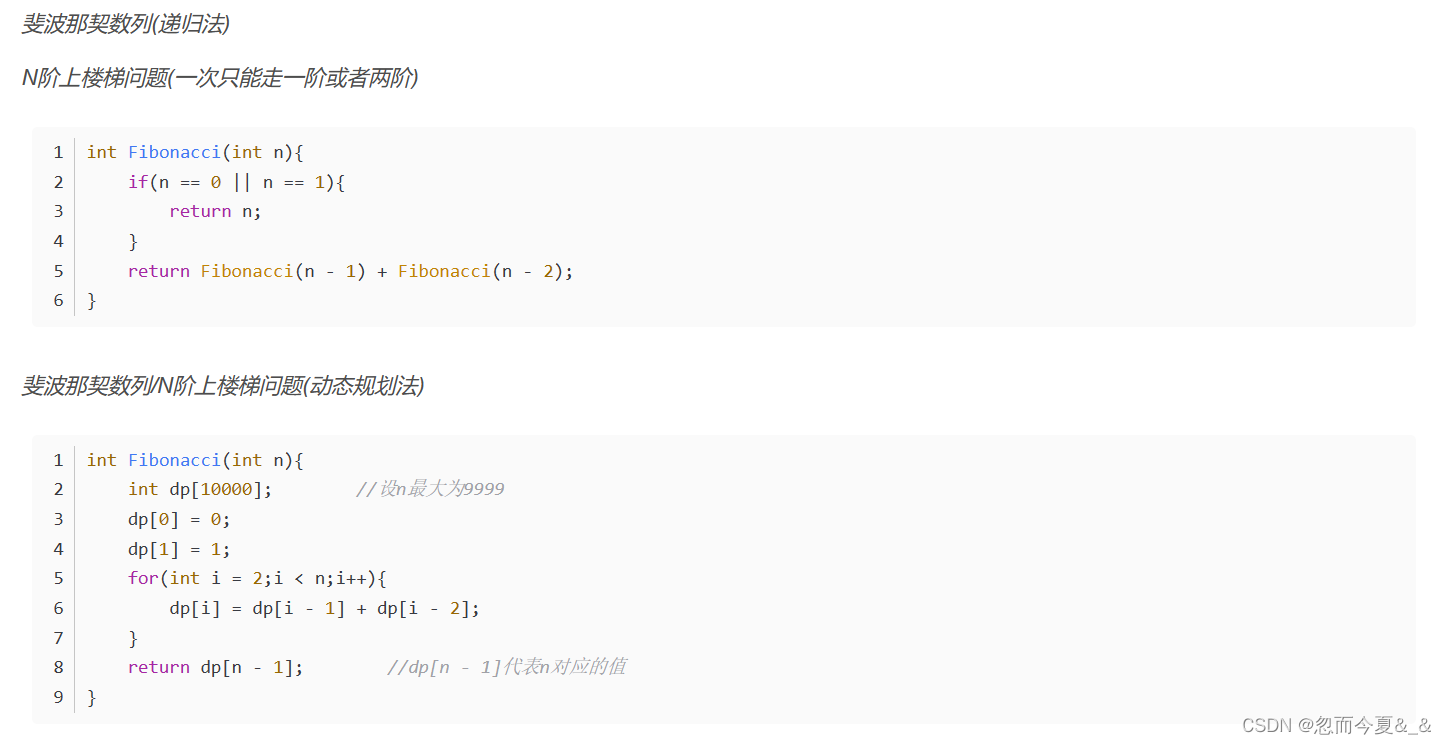
  • 动态规划文章：看一遍就理解：动态规划详解 、 动态规划和递归的区别 。根据下面的代码可以更加直观地理解动态规划和递归的区别与相似之处。
    在这里插入图片描述
词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：VR全景展会丨探索未来，重塑现实，领域虚拟现实新篇章！

下一篇：hjr-详细说一下Redis集群

相关内容

热门资讯

【实验报告】实验一 图像的... 实验目的熟悉Matlab图像运算的基础——矩阵运算；熟悉图像矩阵的显示方法࿰...
MATLAB | 全网最详细网... 一篇超超超长，超超超全面网络图绘制教程，本篇基本能讲清楚所有绘制要点&#...
大模型落地比趋势更重要，NLP... 全球很多人都开始相信，以ChatGPT为代表的大模型，将带来一场NLP领...
Linux学习之端口、网络协议... 端口：设备与外界通讯交流的出口 网络协议： 　　网络协议是指计算机通信网...
kuernetes 资源对象分... 文章目录1. pod 状态1.1 容器启动错误类型1.2 ImagePullBackOff 错误1....
STM32实战项目-数码管 程序实现功能： 1、上电后，数码管间隔50ms计数； 2、...
TM1638和TM1639差异... TM1638和TM1639差异说明 ✨本文不涉及具体的单片机代码驱动内容，值针对芯...
Qt+MySql开发笔记：Qt... 若该文为原创文章，转载请注明原文出处 本文章博客地址：https://h...
Java内存模型中的happe... 第29讲 | Java内存模型中的happen-before是什么？ Java 语言...
《扬帆优配》算力概念股大爆发，... 3月22日，9股封单金额超亿元，工业富联、鸿博股份、鹏鼎控股分别为3.0...
CF1763D Valid B... CF1763D Valid Bitonic Permutations 题目大意 拱形排列࿰...
SQL语法 DDL、DML、D... 文章目录1 SQL通用语法2 SQL分类3 DDL 数据定义语言3.1 数据库操作3.2 表操作3....
文心一言 VS ChatGPT... 3月16号，百度正式发布了『文心一言』，这是国内公司第一次发布类Chat...
CentOS8提高篇5：磁盘分...        首先需要在虚拟机中模拟添加一块新的硬盘设备，然后进行分区、格式化、挂载等...
Linux防火墙——SNAT、... 目录 NAT 一、SNAT策略及作用 1、概述 SNAT应用环境 SNAT原理 SNAT转换前提条...
部署+使用集群的算力跑CPU密... 我先在开头做一个总结，表达我最终要做的事情和最终环境是如何的，然后我会一...
Uploadifive 批量文... Uploadifive 批量文件上传_uploadifive 多个上传按钮_asing1elife的...
C++入门语法基础 文章目录：1. 什么是C++2. 命名空间2.1 域的概念2.2 命名...
2023年全国DAMA-CDG... DAMA认证为数据管理专业人士提供职业目标晋升规划，彰显了职业发展里程碑及发展阶梯定义...
php实现助记词转TRX，ET... TRX助记词转地址网上都是Java，js或其他语言开发的示例，一个简单的...
【分割数据集操作集锦】毕设记录 1. 按要求将CSV文件转成json文件 有时候一些网络模型的源码会有data.json这样的文件里...
Postman接口测试之断言 如果你看文字部分还是不太理解的话，可以看看这个视频，详细介绍postma...
前端学习第三阶段-第4章 jQ... 4-1 jQuery介绍及常用API导读 01-jQuery入门导读 02-JavaScri...
4、linux初级——Linu... 目录 一、用CRT连接开发板 1、安装CRT调试工具 2、连接开发板 3、开机后ctrl+c...
Urban Radiance ... Urban Radiance Fields:城市辐射场 摘要：这项工作的目标是根据扫描...
天干地支（Java） 题目描述 古代中国使用天干地支来记录当前的年份。 天干一共有十个，分别为：...
SpringBoot雪花ID长... Long类型精度丢失 最近项目中使用雪花ID作为主键，雪花ID是19位Long类型数...
对JSP文件的理解 JSP是java程序。（JSP本质还是一个Servlet） JSP是&#...
【03173】2021年4月高... 一、单向填空题1、大量应用软件开发工具，开始于A、20世纪70年代B、20世纪 80年...
LeetCode5.最长回文子... 目录题目链接题目分析解题思路暴力中心向两边拓展搜索 题目链接 链接 题目分析 简单来说࿰...