Ripser.py学习 (8)：莫比乌斯带与系数域 (Moebius Strip And The Field of Coefficients)
创始人
2025-06-01 08:04:19

文章目录

  • 1 概述
  • 2 测试数据

1 概述

本节展示系数域如何影响H1H_1H1​同伦。这个例子，与总是使用Z/2\mathbb{Z}/2Z/2（二进制）系数的常见约定相反，可能有充分的理由使用其他字段，尤其是在有扭曲的情况下。

以下是一些必须库：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from ripser import ripser
from persim import plot_diagrams

2 测试数据

现在创建一个封闭环，可以理解为2D环嵌入到3D空间：

  1. 围绕大圈每转一圈，让环围绕小圈（“内管”部分）运行两次；
  2. 分别给定大圈和小圈的半径RRR和rrr，采样如下参数的曲线：

x(t)=(R+rcos⁡(2t))cos⁡(t)y(t)=(R+rcos⁡(2t))sin⁡(t)z(t=rsin⁡(2t))\begin{aligned} &x(t)=(R+r\cos(2t))\cos(t)\\ &y(t)=(R+r\cos(2t))\sin(t)\\ &z(t=r\sin(2t)) \end{aligned} ​x(t)=(R+rcos(2t))cos(t)y(t)=(R+rcos(2t))sin(t)z(t=rsin(2t))​代码如下：

# 步骤1：曲线设置
N = 100  # 采样点的数量
R = 4    # 大环半径
r = 1    # 小环半径
X = np.zeros((N, 3))
t = np.linspace(0, 2*np.pi, N)
X[:, 0] = (R + r*np.cos(2*t))*np.cos(t)
X[:, 1] = (R + r*np.cos(2*t))*np.sin(t)
X[:, 2] = r*np.sin(2*t)

接着绘制持续图和数据图：

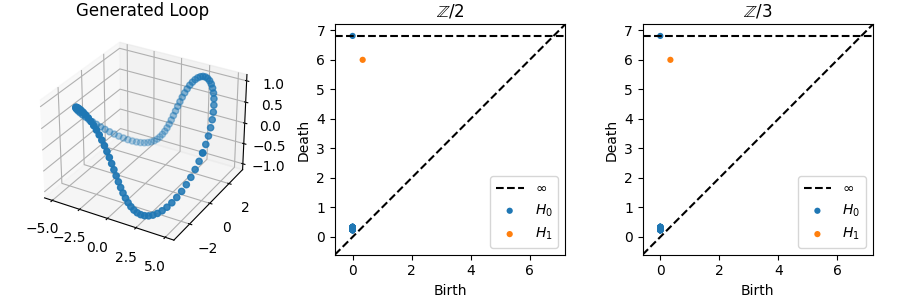
尽管该环很弯曲，H1H_1H1​上只有一个类，且Z/2\mathbb{Z}/2Z/2和Z/3\mathbb{Z}/3Z/3的持续同伦图是一样，即只有一个类在0处初始。

对此，数据的生成公式修改为：
x(t)=(R+rcos⁡(t))cos⁡(2t)y(t)=(R+rcos⁡(t))sin⁡(2t)z(t=rsin⁡(2t))\begin{aligned} &x(t)=(R+r\cos(t))\cos(2t)\\ &y(t)=(R+r\cos(t))\sin(2t)\\ &z(t=r\sin(2t)) \end{aligned} ​x(t)=(R+rcos(t))cos(2t)y(t)=(R+rcos(t))sin(2t)z(t=rsin(2t))​代码如下：

X[:, 0] = (R + r*np.cos(t))*np.cos(2*t)
X[:, 1] = (R + r*np.cos(t))*np.sin(2*t)
X[:, 2] = r*np.sin(t)

输出如下：

词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：【真八股 | 华为OD技术面试】Java都有哪些锁，讲讲MVC，红黑树，常见的异常等问题

下一篇：黄鹤使用说明书-主动给下级当好工具人

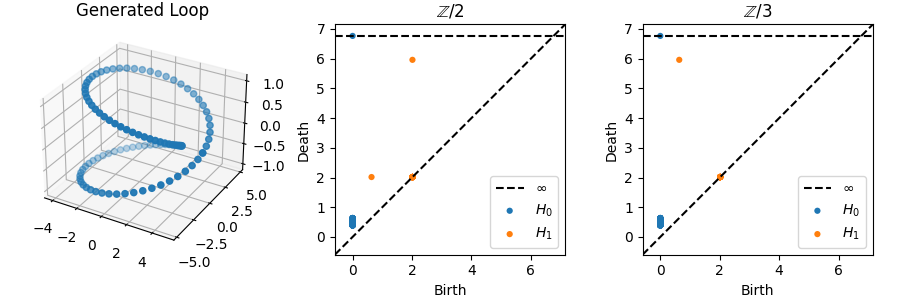
相关内容

热门资讯

【实验报告】实验一 图像的... 实验目的熟悉Matlab图像运算的基础——矩阵运算；熟悉图像矩阵的显示方法࿰...
MATLAB | 全网最详细网... 一篇超超超长，超超超全面网络图绘制教程，本篇基本能讲清楚所有绘制要点&#...
大模型落地比趋势更重要，NLP... 全球很多人都开始相信，以ChatGPT为代表的大模型，将带来一场NLP领...
Linux学习之端口、网络协议... 端口：设备与外界通讯交流的出口 网络协议： 　　网络协议是指计算机通信网...
kuernetes 资源对象分... 文章目录1. pod 状态1.1 容器启动错误类型1.2 ImagePullBackOff 错误1....
STM32实战项目-数码管 程序实现功能： 1、上电后，数码管间隔50ms计数； 2、...
TM1638和TM1639差异... TM1638和TM1639差异说明 ✨本文不涉及具体的单片机代码驱动内容，值针对芯...
Qt+MySql开发笔记：Qt... 若该文为原创文章，转载请注明原文出处 本文章博客地址：https://h...
Java内存模型中的happe... 第29讲 | Java内存模型中的happen-before是什么？ Java 语言...
《扬帆优配》算力概念股大爆发，... 3月22日，9股封单金额超亿元，工业富联、鸿博股份、鹏鼎控股分别为3.0...
CF1763D Valid B... CF1763D Valid Bitonic Permutations 题目大意 拱形排列࿰...
SQL语法 DDL、DML、D... 文章目录1 SQL通用语法2 SQL分类3 DDL 数据定义语言3.1 数据库操作3.2 表操作3....
文心一言 VS ChatGPT... 3月16号，百度正式发布了『文心一言』，这是国内公司第一次发布类Chat...
CentOS8提高篇5：磁盘分...        首先需要在虚拟机中模拟添加一块新的硬盘设备，然后进行分区、格式化、挂载等...
Linux防火墙——SNAT、... 目录 NAT 一、SNAT策略及作用 1、概述 SNAT应用环境 SNAT原理 SNAT转换前提条...
部署+使用集群的算力跑CPU密... 我先在开头做一个总结，表达我最终要做的事情和最终环境是如何的，然后我会一...
Uploadifive 批量文... Uploadifive 批量文件上传_uploadifive 多个上传按钮_asing1elife的...
C++入门语法基础 文章目录：1. 什么是C++2. 命名空间2.1 域的概念2.2 命名...
2023年全国DAMA-CDG... DAMA认证为数据管理专业人士提供职业目标晋升规划，彰显了职业发展里程碑及发展阶梯定义...
php实现助记词转TRX，ET... TRX助记词转地址网上都是Java，js或其他语言开发的示例，一个简单的...
【分割数据集操作集锦】毕设记录 1. 按要求将CSV文件转成json文件 有时候一些网络模型的源码会有data.json这样的文件里...
Postman接口测试之断言 如果你看文字部分还是不太理解的话，可以看看这个视频，详细介绍postma...
前端学习第三阶段-第4章 jQ... 4-1 jQuery介绍及常用API导读 01-jQuery入门导读 02-JavaScri...
4、linux初级——Linu... 目录 一、用CRT连接开发板 1、安装CRT调试工具 2、连接开发板 3、开机后ctrl+c...
Urban Radiance ... Urban Radiance Fields:城市辐射场 摘要：这项工作的目标是根据扫描...
天干地支（Java） 题目描述 古代中国使用天干地支来记录当前的年份。 天干一共有十个，分别为：...
SpringBoot雪花ID长... Long类型精度丢失 最近项目中使用雪花ID作为主键，雪花ID是19位Long类型数...
对JSP文件的理解 JSP是java程序。（JSP本质还是一个Servlet） JSP是&#...
【03173】2021年4月高... 一、单向填空题1、大量应用软件开发工具，开始于A、20世纪70年代B、20世纪 80年...
LeetCode5.最长回文子... 目录题目链接题目分析解题思路暴力中心向两边拓展搜索 题目链接 链接 题目分析 简单来说࿰...