这里写目录标题

• 1 马尔可夫性质
• 2 马尔可夫过程
• 3 马尔可夫奖励过程（Markov reward process, MRP）
• • 3.1 MRP的贝尔曼方程
  • 3.2 MRP的贝尔曼方程求解方法
  • 3.3 总结
• 4 马尔可夫决策过程（Markov decision process, MDP）
• • 4.1 MDP状态价值函数贝尔曼方程推导
  • 4.2 MDP动作价值函数
  • 4.3 动作价值函数&状态价值函数的关系
  • 4.4 MDP寻找最优策略&贝尔曼最优公式
  • 4.4 总结
• 5 强化学习引入MDP的原因

1 马尔可夫性质

马尔可夫性质（Markov property）是指一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态。即：P(St+1∣St,St−1,...,S1)=P(St+1∣St)P(S_{t+1}|S_t,S_{t-1},...,S_1)=P(S_{t+1}|S_t)P(St+1​∣St​,St−1​,...,S1​)=P(St+1​∣St​)

2 马尔可夫过程

马尔可夫链/过程是满足马尔可夫性质的随机过程，为一个两元组：

• SSS 是状态集合s∈Ss \in Ss∈S。
• PPP是状态转移矩阵。用状态转移矩阵PPP来描述在状态sts_tst​到达其他状态的概率p(st+1∣st)p(s_{t+1} \mid s_t)p(st+1​∣st​)
  P=(p(s1∣s1)p(s2∣s1)…p(sN∣s1)p(s1∣s2)p(s2∣s2)…p(sN∣s2)⋮⋮⋱⋮p(s1∣sN)p(s2∣sN)…p(sN∣sN))\boldsymbol{P}=\left(\begin{array}{cccc} p\left(s_{1} \mid s_{1}\right) & p\left(s_{2} \mid s_{1}\right) & \ldots & p\left(s_{N} \mid s_{1}\right) \\ p\left(s_{1} \mid s_{2}\right) & p\left(s_{2} \mid s_{2}\right) & \ldots & p\left(s_{N} \mid s_{2}\right) \\ \vdots & \vdots & \ddots & \vdots \\ p\left(s_{1} \mid s_{N}\right) & p\left(s_{2} \mid s_{N}\right) & \ldots & p\left(s_{N} \mid s_{N}\right) \end{array}\right)P=​p(s1​∣s1​)p(s1​∣s2​)⋮p(s1​∣sN​)​p(s2​∣s1​)p(s2​∣s2​)⋮p(s2​∣sN​)​……⋱…​p(sN​∣s1​)p(sN​∣s2​)⋮p(sN​∣sN​)​​

3 马尔可夫奖励过程（Markov reward process, MRP）

马尔可夫奖励过程=马尔可夫链+奖励，为一个四元组：

• SSS 是状态集合s∈Ss \in Ss∈S。
• PPP是状态转移矩阵。用状态转移矩阵PPP来描述在状态sts_tst​到达其他状态的概率p(st+1∣st)p(s_{t+1} \mid s_t)p(st+1​∣st​)。
• RRR是奖励函数，R(st=s)=E[rt∣st=s]R(s_t=s)=\mathbb{E} [r_t \mid s_t = s]R(st​=s)=E[rt​∣st​=s]。
• γ\gammaγ是折扣率。

3.1 MRP的贝尔曼方程

MRP中引入了奖励的概念，因此对于任意状态∀s∈S\forall s \in S∀s∈S可以计算该状态的回报v(s)v(s)v(s)，推导出MRP贝尔曼方程如下：
vπ(s)=E[Gt∣St=s]=E[Rt+1+γGt+1∣St=s]=E[Rt+1∣St=s]+γE[Gt+1∣St=s]=R(s)+γ∑s′p(s′∣s)v(s′)\begin{align} v_\pi(s) &=\mathbb{E}[G_t|S_t=s] \\ &=\mathbb{E}[R_{t+1}+\gamma G_{t+1} |S_t=s]\\ &=\textcolor{red}{\mathbb{E} [R_{t+1}|S_t=s]}+ \gamma \textcolor{blue}{\mathbb{E}[G_{t+1} |S_t=s]} \\ &=R(s)+\gamma \sum_{s'} p(s' \mid s) v(s') \end{align}vπ​(s)​=E[Gt​∣St​=s]=E[Rt+1​+γGt+1​∣St​=s]=E[Rt+1​∣St​=s]+γE[Gt+1​∣St​=s]=R(s)+γs′∑​p(s′∣s)v(s′)​​

除了一般形式，我们还需要矩阵形式：
v=r+γPv\begin{align} \bold{v} = \bold{r}+ \gamma \bold{P} \bold{v}\end{align}v=r+γPv​​
我们可以把它展开（假设有4个状态）
[vπ(s1)vπ(s2)vπ(s3)vπ(s4)]⏟vπ=[rπ(s1)rπ(s2)rπ(s3)rπ(s4)]⏟rπ+γ[pπ(s1∣s1)pπ(s2∣s1)pπ(s3∣s1)pπ(s4∣s1)pπ(s1∣s2)pπ(s2∣s2)pπ(s3∣s2)pπ(s4∣s2)pπ(s1∣s3)pπ(s2∣s3)pπ(s3∣s3)pπ(s4∣s3)pπ(s1∣s4)pπ(s2∣s4)pπ(s3∣s4)pπ(s4∣s4)]⏟Pπ[vπ(s1)vπ(s2)vπ(s3)vπ(s4)]⏟vπ.\underbrace{\left[\begin{array}{l} v_\pi\left(s_1\right) \\ v_\pi\left(s_2\right) \\ v_\pi\left(s_3\right) \\ v_\pi\left(s_4\right) \end{array}\right]}_{v_\pi}=\underbrace{\left[\begin{array}{l} r_\pi\left(s_1\right) \\ r_\pi\left(s_2\right) \\ r_\pi\left(s_3\right) \\ r_\pi\left(s_4\right) \end{array}\right]}_{r_\pi}+\gamma \underbrace{\left[\begin{array}{llll} p_\pi\left(s_1 \mid s_1\right) & p_\pi\left(s_2 \mid s_1\right) & p_\pi\left(s_3 \mid s_1\right) & p_\pi\left(s_4 \mid s_1\right) \\ p_\pi\left(s_1 \mid s_2\right) & p_\pi\left(s_2 \mid s_2\right) & p_\pi\left(s_3 \mid s_2\right) & p_\pi\left(s_4 \mid s_2\right) \\ p_\pi\left(s_1 \mid s_3\right) & p_\pi\left(s_2 \mid s_3\right) & p_\pi\left(s_3 \mid s_3\right) & p_\pi\left(s_4 \mid s_3\right) \\ p_\pi\left(s_1 \mid s_4\right) & p_\pi\left(s_2 \mid s_4\right) & p_\pi\left(s_3 \mid s_4\right) & p_\pi\left(s_4 \mid s_4\right) \end{array}\right]}_{P_\pi} \underbrace{\left[\begin{array}{l} v_\pi\left(s_1\right) \\ v_\pi\left(s_2\right) \\ v_\pi\left(s_3\right) \\ v_\pi\left(s_4\right) \end{array}\right]}_{v_\pi} .vπ​​vπ​(s1​)vπ​(s2​)vπ​(s3​)vπ​(s4​)​​​​=rπ​​rπ​(s1​)rπ​(s2​)rπ​(s3​)rπ​(s4​)​​​​+γPπ​​pπ​(s1​∣s1​)pπ​(s1​∣s2​)pπ​(s1​∣s3​)pπ​(s1​∣s4​)​pπ​(s2​∣s1​)pπ​(s2​∣s2​)pπ​(s2​∣s3​)pπ​(s2​∣s4​)​pπ​(s3​∣s1​)pπ​(s3​∣s2​)pπ​(s3​∣s3​)pπ​(s3​∣s4​)​pπ​(s4​∣s1​)pπ​(s4​∣s2​)pπ​(s4​∣s3​)pπ​(s4​∣s4​)​​​​vπ​​vπ​(s1​)vπ​(s2​)vπ​(s3​)vπ​(s4​)​​​​.

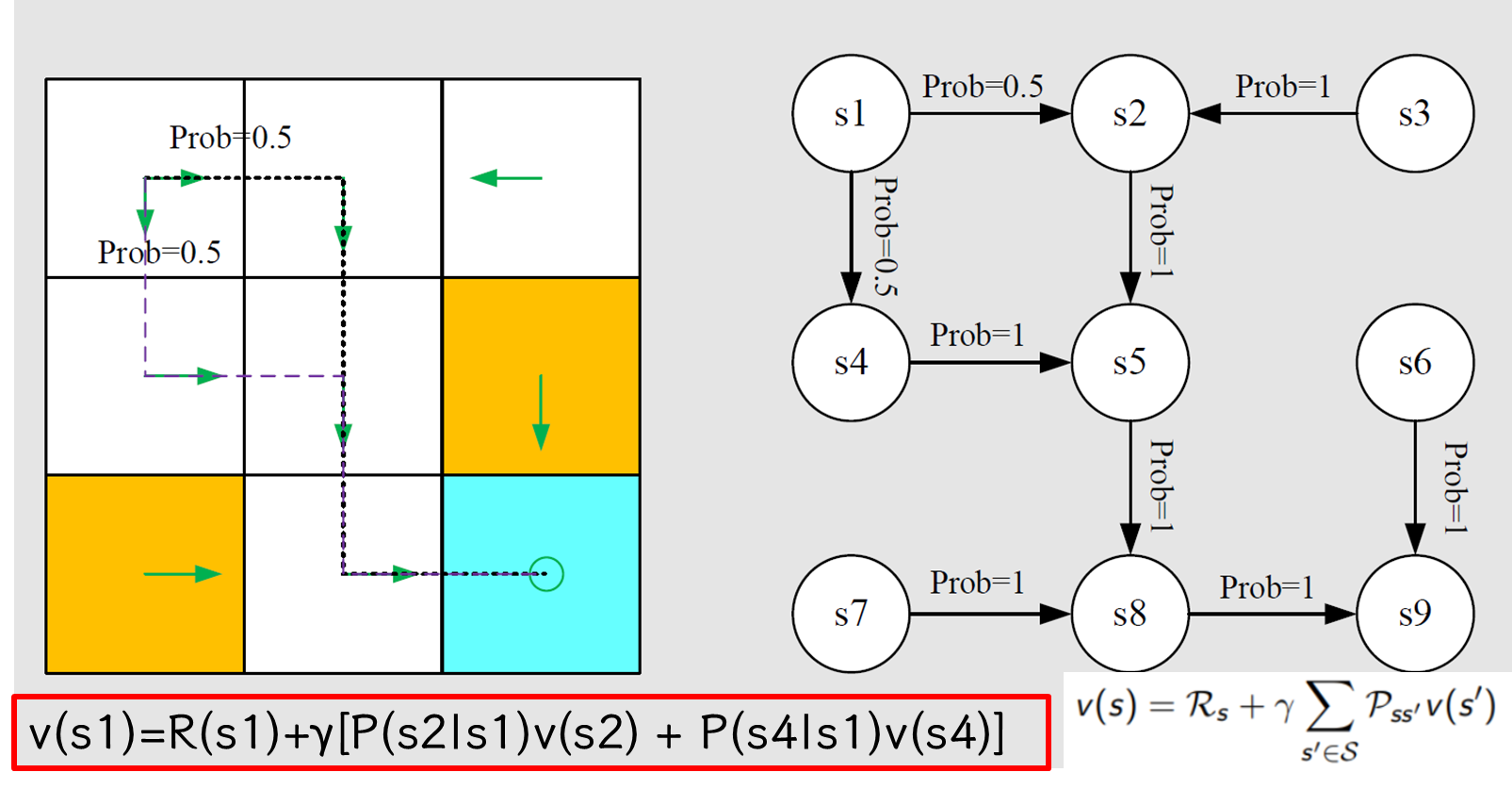
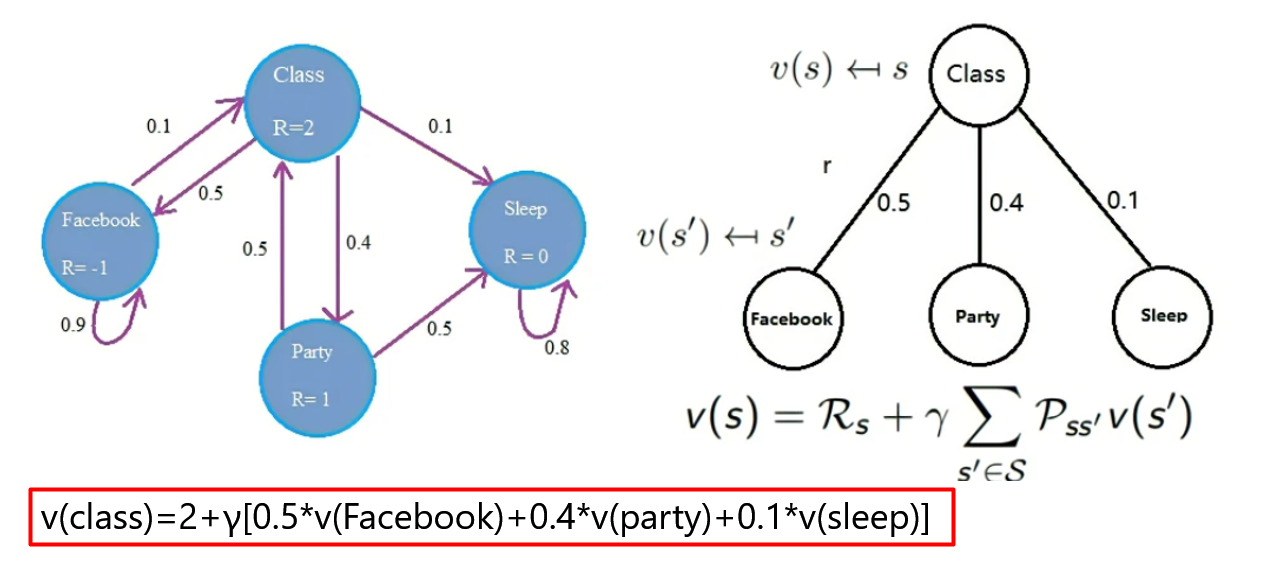
3.2 MRP的贝尔曼方程求解方法

式（5）是一个线性方程组，因此可以直接得到解析解：

v=r+γPv(I−γP)v=rv=(I−γP)−1r\begin{align} \bold{v}=\bold{r}+\gamma \bold{P}\bold{v}\\ ({\bold{I}}-\gamma \bold{P}) \bold{v}=\bold{r} \\ \bold{v}=(\bold{I}-\gamma \bold{P})^{-1} \bold{r} \end{align} v=r+γPv(I−γP)v=rv=(I−γP)−1r​​
斜体样式
从上式可知，可以通过矩阵逆运算直接求解方程，但矩阵求逆的复杂度为O(n^3),n为状态数。因此，直接求解仅适用于状态空间规模小的MRP。状态空间规模大的MRP的求解通常使用迭代法。常用的迭代方法有：动态规划(Dynamic Programming)、蒙特卡洛评估(Monte-Carlo evaluation)、时序差分学(Temporal-Difference)等

3.3 总结

MRP贝尔曼方程

• 一般形式：
• 矩阵形式：

求解方法：

• 解析法：适应于规模较小的问题
• 迭代方法：适应于规模较大的问题，常用方法有动态规划、蒙特卡洛模拟、时序差分法

4 马尔可夫决策过程（Markov decision process, MDP）

马尔可夫决策过程=马尔可夫奖励过程+动作，MDP是一个五元组

• SSS 是状态空间s∈Ss \in Ss∈S。
• AAA是动作空间a∈Aa \in Aa∈A。
• PPP是状态转移矩阵。用状态转移矩阵PPP来描述，在状态sts_tst​，采取动作ata_tat​，到达其他状态的概率p(st+1∣st=s,at=a)p(s_{t+1} \mid s_t=s, a_t=a)p(st+1​∣st​=s,at​=a)。
• RRR是奖励函数，R(st=s,at=a)=E[rt∣st=s,at=a]R(s_t=s, a_t=a)=\mathbb{E} [r_t \mid s_t = s, a_t=a]R(st​=s,at​=a)=E[rt​∣st​=s,at​=a]。
• γ\gammaγ是折扣率。

Markov decison process中，Markov代表的是马尔可夫性质（无后效性）；decision代表的是策略（Policy），在某个状态s，采取动作a的概率是π(a∣s)=P(at=a∣st=s)\pi(a|s)=P(a_t=a \mid s_t = s)π(a∣s)=P(at​=a∣st​=s)；process代表的是状态转移概率

4.1 MDP状态价值函数贝尔曼方程推导

MDP中因为有了策略π\piπ,状态价值函数vπ(s)v_{\pi}(s)vπ​(s)是从状态s开始，执行策略所获得的回报的期望。
vπ(s)=E[Gt∣St=s]\begin{align} v_\pi(s)=\mathbb{E}[G_t|S_t=s] \end{align}vπ​(s)=E[Gt​∣St​=s]​​

根据状态价值的定义，推导Bellman equation：
vπ(s)=E[Gt∣St=s]=E[Rt+1+γGt+1∣St=s]=E[Rt+1∣St=s]+γE[Gt+1∣St=s]=∑aπ(a∣s)E[Rt+1∣St=s,At=a]+γ∑s′E[Gt+1∣St=s,St+1=s′]p(s′∣s)=∑aπ(a∣s)Rsa+γ∑s′vπ(s′)∑aPss′aπ(s∣a)=∑aπ(a∣s)(Rsa+γ∑s′Pss′avπ(s′))\begin{align} v_\pi(s) &=\mathbb{E}[G_t|S_t=s] \\ &=\mathbb{E}[R_{t+1}+\gamma G_{t+1} |S_t=s]\\ &=\textcolor{red}{\mathbb{E} [R_{t+1}|S_t=s]}+ \gamma \textcolor{blue}{\mathbb{E}[G_{t+1} |S_t=s]} \\ &=\textcolor{red}{ \sum_{a}{\pi(a \mid s) \mathbb{E}[R_{t+1}|S_t=s,A_t=a]}}+\gamma \textcolor{blue}{ \sum_{s'}{ \mathbb{E}[G_{t+1} | S_t=s,S_{t+1}=s' ] p(s'|s)}}\\ &=\textcolor{red}{\sum_a \pi( a \mid s)R_s^a}+ \gamma \textcolor{blue}{\sum_{s'}{v_{\pi}(s') \sum_{a}{P_{ss'}^a \pi(s|a)}}}\\ &= \sum_{a}{\pi(a \mid s)} \left( R_s^a +\gamma \sum_{s'}{P_{ss'}^a}v_{\pi}(s') \right) \end{align}vπ​(s)​=E[Gt​∣St​=s]=E[Rt+1​+γGt+1​∣St​=s]=E[Rt+1​∣St​=s]+γE[Gt+1​∣St​=s]=a∑​π(a∣s)E[Rt+1​∣St​=s,At​=a]+γs′∑​E[Gt+1​∣St​=s,St+1​=s′]p(s′∣s)=a∑​π(a∣s)Rsa​+γs′∑​vπ​(s′)a∑​Pss′a​π(s∣a)=a∑​π(a∣s)(Rsa​+γs′∑​Pss′a​vπ​(s′))​​

除了一般形式，我们还需要矩阵形式：
vπ(s)=∑aπ(a∣s)(Rsa+γ∑s′Pss′avπ(s′))=∑aπ(a∣s)Rsa+γ∑s′vπ(s′)∑aPss′aπ(s∣a)=rπ(s)+γ∑s′pπ(s′∣s)vπ(s′)\begin{align} v_\pi(s) &= \sum_{a}{\pi(a \mid s)} \left( R_s^a +\gamma \sum_{s'}{P_{ss'}^a}v_{\pi}(s') \right)\\ &=\textcolor{red}{ \sum_a{\pi(a \mid s)} R_s^a }+ \gamma \textcolor{blue}{\sum_{s'}{v_{\pi}(s') \sum_{a}{P_{ss'}^a \pi(s \mid a)}}}\\ &=r_\pi (s)+\gamma \sum_{s'}{p_\pi(s' \mid s)v_\pi(s')} \end{align}vπ​(s)​=a∑​π(a∣s)(Rsa​+γs′∑​Pss′a​vπ​(s′))=a∑​π(a∣s)Rsa​+γs′∑​vπ​(s′)a∑​Pss′a​π(s∣a)=rπ​(s)+γs′∑​pπ​(s′∣s)vπ​(s′)​​
假设状态空间为{si}i=1n\{s_i\}_{i=1}^n{si​}i=1n​，对sis_isi​，其Bellman equation为：
vπ(si)=rπ(si)+γ∑sjpπ(sj∣si)vπ(sj)\begin{align} v_{\pi}\left(s_{i}\right)=r_{\pi}\left(s_{i}\right)+\gamma \sum_{s_{j}} p_{\pi}\left(s_{j} \mid s_{i}\right) v_{\pi}\left(s_{j}\right)\end{align}vπ​(si​)=rπ​(si​)+γsj​∑​pπ​(sj​∣si​)vπ​(sj​)​​
将矩阵向量形式表示所有状态的Bellman equation：
vπ=rπ+γPπvπ\begin{align} v_\pi=r_\pi+\gamma P_\pi v_\pi\end{align}vπ​=rπ​+γPπ​vπ​​​
其中，

• vπ=[vπ(s1),…,vπ(sn)]T∈Rnv_{\pi}=\left[v_{\pi}\left(s_{1}\right), \ldots, v_{\pi}\left(s_{n}\right)\right]^{T} \in \mathbb{R}^{n}vπ​=[vπ​(s1​),…,vπ​(sn​)]T∈Rn
• rπ=[rπ(s1),…,rπ(sn)]T∈Rnr_{\pi}=\left[r_{\pi}\left(s_{1}\right), \ldots, r_{\pi}\left(s_{n}\right)\right]^{T} \in \mathbb{R}^{n}rπ​=[rπ​(s1​),…,rπ​(sn​)]T∈Rn
• Pπ∈Rn∗nP_\pi \in \mathbb{R}^{n*n}Pπ​∈Rn∗n，where [Pπ]ij=pπ(sj∣si)[P_\pi ]_{ij}= p_\pi(s_j|s_i)[Pπ​]ij​=pπ​(sj​∣si​)，为状态转移矩阵

4.2 MDP动作价值函数

动作价值函数定义为：
qπ(s,a)=E[Gt∣St=s,At=a]=∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vπ(s′)\begin{align} q_\pi{(s,a)} &=\mathbb{E}[G_t|S_t=s,A_t=a] \\ &= \sum_r{p(r|s,a)r+\gamma \sum_{s'}{p(s'|s,a)v_\pi(s')}} \end{align}qπ​(s,a)​=E[Gt​∣St​=s,At​=a]=r∑​p(r∣s,a)r+γs′∑​p(s′∣s,a)vπ​(s′)​​

4.3 动作价值函数&状态价值函数的关系

根据状态价值函数的定义：
E[Gt∣St=s]⏟vπ(s)=∑aE[Gt∣St=s,At=a]⏟qπ(s,a)π(a∣s)\begin{align} \underbrace{\mathbb{E}\left[G_t \mid S_t=s\right]}_{v_\pi(s)}=\sum_a \underbrace{\mathbb{E}\left[G_t \mid S_t=s, A_t=a\right]}_{q_\pi(s, a)} \pi(a \mid s) \end{align}vπ​(s)E[Gt​∣St​=s]​​=a∑​qπ​(s,a)E[Gt​∣St​=s,At​=a]​​π(a∣s)​​
因此状态价值函数和动作价值函数的关系为：
vπ(s)=∑aπ(a∣s)qπ(s,a)\begin{align} \textcolor{red}{ v_\pi(s) } =\sum_{a}{\pi(a|s) \textcolor{red}{q_\pi(s,a)}} \end{align}vπ​(s)=a∑​π(a∣s)qπ​(s,a)​​

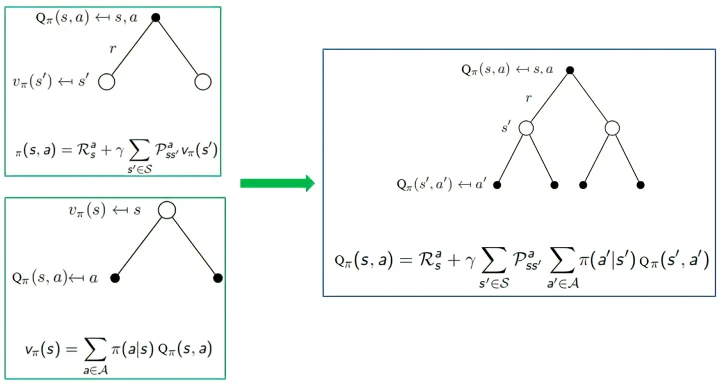
backup diagram是算法的图形化表示，通过图形表示状态，动作，状态转移，奖励等。下图中，空心较大圆圈表示状态，黑色实心小圆表示的是动作，连接状态和动作的线条仅仅把该状态以及该状态下可以采取的动作关联起来，黑色小圆和后续状态之间的连线为即时奖励。

状态价值函数和动作价值函数的关系：

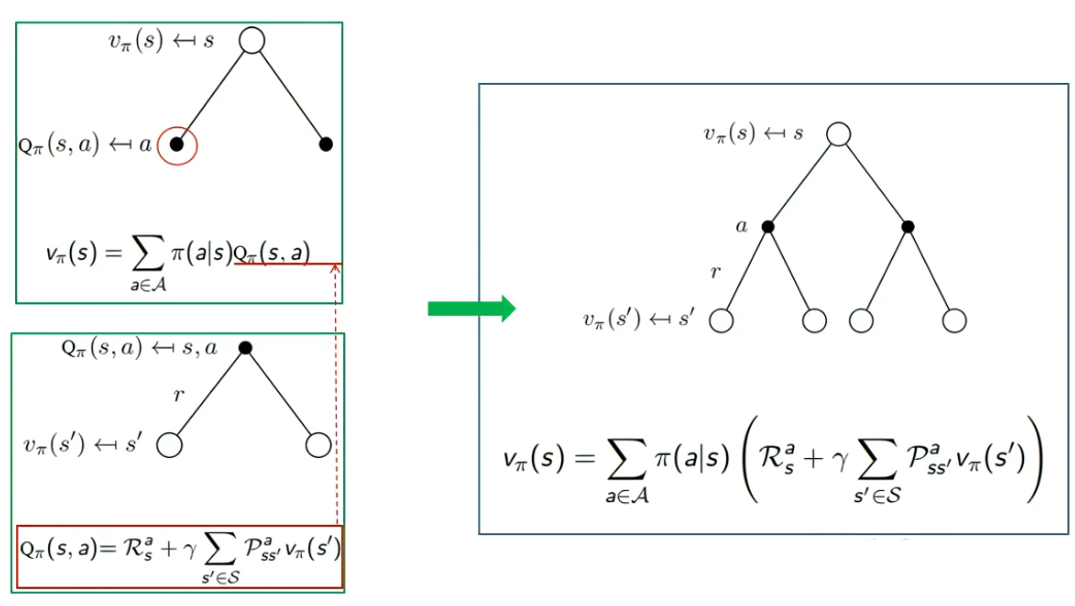
动作价值函数和状态价值函数的关系：

4.4 MDP寻找最优策略&贝尔曼最优公式

如果已有马尔可夫决策过程，如何寻找最优策略？贝尔曼公式中策略pi是给定。 若策略pi没有给出，则需要先确定最优策略pi，此时就变成了贝尔曼最优公式，记：

v∗(s)=max⁡πvπ(s)=max⁡π∑aπ(a∣s)(∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vπ(s′)),∀s∈S=max⁡π∑aπ(a∣s)qπ(s,a)s∈S\begin{align} v_*(s) &= \max_\pi v_\pi (s) \\ & =\max _{\pi} \sum_{a} \pi(a \mid s) \left(\sum_{r} p(r \mid s, a) r+\gamma \sum_{s^{\prime}} p\left(s^{\prime} \mid s, a\right) v_\pi\left(s^{\prime}\right)\right), \quad \forall s \in \mathcal{S} \\ & =\max _{\pi} \sum_{a} \pi(a \mid s) q_\pi(s, a) \quad s \in \mathcal{S} \end{align}v∗​(s)​=πmax​vπ​(s)=πmax​a∑​π(a∣s)(r∑​p(r∣s,a)r+γs′∑​p(s′∣s,a)vπ​(s′)),∀s∈S=πmax​a∑​π(a∣s)qπ​(s,a)s∈S​​

注意：

• p(r∣s,a),p(s′∣s,a)p\left( r \mid s,a\right),p\left(s^{\prime} \mid s,a \right)p(r∣s,a),p(s′∣s,a)为已知
• v(s),v(s′)v\left(s\right),v\left( s^{\prime}\right)v(s),v(s′)是待求解的未知量
• 策略π(a∣s)\pi(a \mid s)π(a∣s)为未知

最优策略是使得状态动作价值最大的vπ(s)v_\pi(s)vπ​(s)策略：
π∗(s)=arg max⁡πvπ(s)\begin{align} \pi_*(s)=\argmax_\pi v_\pi(s)\end{align}π∗​(s)=πargmax​vπ​(s)​​

π∗(a∣s)={1if a=arg⁡max⁡a∈Aq∗(s,a)0else \begin{align} \pi_{*}(a \mid s)=\left\{\begin{array}{ll} 1 & \text { if } a=\arg \max _{a \in A} q_{*}(s, a) \\ 0 & \text { else } \end{array}\right.\end{align}π∗​(a∣s)={10​ if a=argmaxa∈A​q∗​(s,a) else ​​​

除了一般形式：
vπ(s)=max⁡π∑aπ(a∣s)(∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vπ(s′))⏟q(s,a),∀s∈S\begin{align}v_\pi (s)=\max _{\pi} \sum_{a} \pi(a \mid s) \underbrace{\left(\sum_{r} p(r \mid s, a) r+\gamma \sum_{s^{\prime}} p\left(s^{\prime} \mid s, a\right) v_\pi\left(s^{\prime}\right)\right)}_{q(s, a)}, \quad \forall s \in \mathcal{S} \end{align}vπ​(s)=πmax​a∑​π(a∣s)q(s,a)(r∑​p(r∣s,a)r+γs′∑​p(s′∣s,a)vπ​(s′))​​,∀s∈S​​
我们还需要矩阵向量形式：
v=max⁡π(rπ+γPπv)\begin{align} \bold v=\max_{\pi}(\bold r_\pi+\gamma \bold{P_\pi} \bold v) \end{align}v=πmax​(rπ​+γPπ​v)​​
贝尔曼最优公式的解一定存在，且该解是唯一的，这里不做证明。

求解算法：解析解（不推荐）；迭代方法

4.4 总结

• 状态价值函数定义：vπ(s)=E[Gt∣St=s]v_\pi(s)=\mathbb{E}[G_t|S_t=s]vπ​(s)=E[Gt​∣St​=s]
• 动作价值函数定义：qπ(s,a)=E[Gt∣St=s,At=a]q_\pi{(s,a)}=\mathbb{E}[G_t|S_t=s,A_t=a]qπ​(s,a)=E[Gt​∣St​=s,At​=a]
• 贝尔曼方程一般形式：vπ(s)=max⁡π∑aπ(a∣s)(∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vπ(s′))⏟q(s,a),∀s∈Sv_\pi (s)=\max _{\pi} \sum_{a} \pi(a \mid s) \underbrace{\left(\sum_{r} p(r \mid s, a) r+\gamma \sum_{s^{\prime}} p\left(s^{\prime} \mid s, a\right) v_\pi\left(s^{\prime}\right)\right)}_{q(s, a)}, \quad \forall s \in \mathcal{S}vπ​(s)=maxπ​∑a​π(a∣s)q(s,a)(r∑​p(r∣s,a)r+γs′∑​p(s′∣s,a)vπ​(s′))​​,∀s∈S
• 贝尔曼方程矩阵形式：v=max⁡π(rπ+γPπv)v=\max_{\pi}(r_\pi+\gamma P_\pi v)v=maxπ​(rπ​+γPπ​v)，推导出解析解
• 如何求解贝尔曼方程：解析解，迭代的方法

5 强化学习引入MDP的原因

环境的状态转化模型，它可以表示为一个概率模型，即在状态s下采取动作a，转到下一个状态s′的概率，表示为Pss′aP_{ss'}^aPss′a​。