文章目录

• • 累积分布函数定义
  • 示例说明
  • Python 代码实现
  • 需要考虑相等数据吗？

累积分布函数定义

累积分布函数(cumulative distribution function, 缩写 CDF)，定义如下：
F(a)=P⁡(X≤a).F(a)=\operatorname{P}(X\le a). F(a)=P(X≤a).
即累积分布函数表示：对离散变量而言，所有小于等于a的值出现概率的和。
（来源于百度百科）

示例说明

用一个例子来理解累积分布函数：
比如对于一组数据：2, 3, 7, 6, 5, 0
先从小到大进行排序，变为：0, 2, 3, 5, 6, 7
数据的总长度为6
根据定义，对于第1个元素0，在[0, 2, 3, 5, 6, 7]中小于等于0的数有1个(即0，前1个)，CDF值为1/6；
同理，对于第2个元素2，在[0, 2, 3, 5, 6, 7]中小于等于2的数有2个(即0,2，前2个)，CDF值为2/6；
……
同理，对于第6个元素7，在[0, 2, 3, 5, 6, 7]中小于等于7的数有2个(即0,2,3,5,6,7，前6个)，CDF值为6/6；
因此，对于一组长度为length且已排好序的数据，第n个元素的CDF值为n/length。

Python 代码实现

对于给定的一组数据data以及一个值a，对应的CDF值应该为找到所有小于等于a的数据个数再除以数据的总长度：

def cdf(data, a):length = len([i for i in data if i <= a])return length / (len(data))

接下来，计算data的累积分布函数
第一步，对data进行从小到大排序：

sorted_data = np.sort(data)

第二步，计算CDF，可以借助np.arange方法来计算，np.arange接受3个参数，分别为生成数据左边界值、右边界值（注意是左闭右开）、间隔（默认为1），表示生成从1到len(data)，间隔为1的一组等距序列，再除以数据的总长度，即生成从1/len(data)到1的等距序列，即为CDF值：

cumulative_prob = np.arange(1, len(sorted_data) + 1, 1)/float(len(sorted_data))

第三步，绘图：

plt.plot(sorted_data, cumulative_prob)
plt.show()

完整的示例代码如下：

import matplotlib.pyplot as plt
import numpy as npdata = np.array([2, 3, 7, 6, 5, 0])
sorted_data = np.sort(data)
cumulative_prob = np.arange(1, len(sorted_data) + 1, 1)/float(len(sorted_data))
print(sorted_data)
print(cumulative_prob)plt.plot(sorted_data, cumulative_prob)
plt.show()

控制台输出：

[0 2 3 5 6 7]
[0.16666667 0.33333333 0.5        0.66666667 0.83333333 1.        ]

绘图结果：

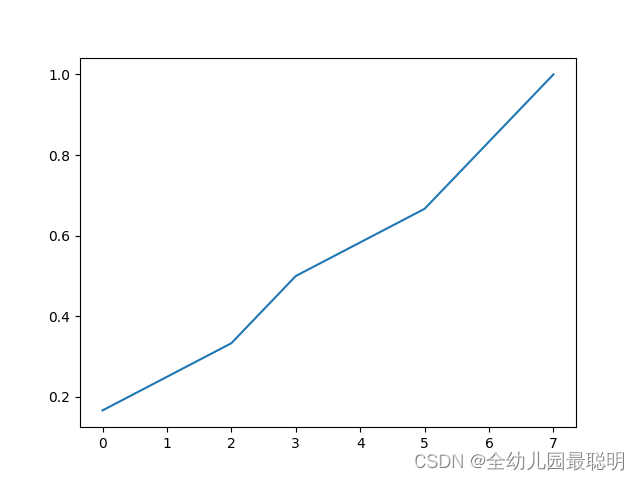
需要考虑相等数据吗？

我们并没有对包含相等数据的情况进行特殊考虑，比如0, 2, 2, 5, 6, 7这组数据中，前一个2得到的CDF值为0.33333333，后一个2得到的CDF值为0.5，显然0.5才是正确的，调用前文的cdf函数也将得到0.5的结果，但是绘图时后面的0.5会覆盖前一个0.33333333，因此绘制出来的图像仍然是正确的。