线性回归-线性神经网络
线性神经网络
注:
该文章为作者学习深度学习笔记,共参考以下两大开源深度学习资料:
- 深度学习(花书)
https://github.com/exacity/deeplearningbook-chinese - 动手学习深度学习(李沐)
https://zh-v2.d2l.ai/
线性回归
线性回归是一种常用的统计分析方法,它可以用来研究一个或多个自变量和因变量之间的线性关系。线性回归的应用非常广泛,例如:
- 在经济学中,线性回归可以用来估计需求函数、生产函数、消费函数等,以及分析各种因素对经济增长、通货膨胀、失业率等的影响。
- 在社会科学中,线性回归可以用来探索教育水平、收入水平、健康状况、政治倾向等变量之间的关系,以及评估政策效果、社会福利、人口变化等问题。
- 在自然科学中,线性回归可以用来建立物理现象、化学反应、生物过程等的数学模型,以及预测未来的发展趋势、优化实验设计、检验假设等。
例如在对收入水平进行线性回归建模时,通过受访者人数(万)和收入水平(美元),来预测群体的平均消费水平,通常需要收集一个真是的数据集,这个数据集里面,包括收入水平,人群数量等等。通常把该数据集称之为训练集(training data set)。每行数据称为样本(sample)。最终预测结果为标签(label)。
通常使用nnn来表示数据集中的样本数。对索引为i的样本,其输入为 x(i)=[x1(i),x2(i)]Tx^{(i)} = [x_1^{(i)},x_2^{(i)}]^Tx(i)=[x1(i),x2(i)]T,其对应的标签为 y(i)y^{(i)}y(i)
线性模型
- 通常线性模型的标识如下:
y^=w1x1+...+wdxd+b.\hat{y} = w_1 x_1 + ... + w_d x_d + b.y^=w1x1+...+wdxd+b.
其中 y^\hat{y}y^ 为预测值,xxx为特征向量,wiw_iwi为权重(weight),b为偏移量(offset)或为截距(intercept) - 或者还可以标识为:
y^=w⊤x+b.\hat{y} = \mathbf{w}^\top \mathbf{x} + b.y^=w⊤x+b.
损失函数
通常对模型进行拟合时,总要定义损失函数(loss function),其能够显示目标与预测值之间的差距,对损失值的定义通常为非负数来显示差距,对于线性回归,损失函数定义如下:
l(i)(w,b)=12(y^(i)−y(i))2.l^{(i)}(\mathbf{w}, b) = \frac{1}{2}(\hat{y}^{(i)} - y^{(i)})^2.l(i)(w,b)=21(y^(i)−y(i))2.
如下图所示:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5adZ2x0h-1679495386406)(null)]](/uploadfile/202506/66b64ffe4aa3964.png)
上述的损失函数是针对单个预测值的,那么对于训练集上nnn个样本的损失值,等价于对所有单个随时之进行求和:
L(w,b)=1n∑i=1nl(i)(w,b)=1n∑i=1n12(w⊤x(i)+b−y(i))2.L(\mathbf{w}, b) =\frac{1}{n}\sum_{i=1}^n l^{(i)}(\mathbf{w}, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2.L(w,b)=n1i=1∑nl(i)(w,b)=n1i=1∑n21(w⊤x(i)+b−y(i))2.
解析解
线性回归的解可以用一个公式简单地表达出来, 这类解叫作解析解(analytical solution)。如:
w∗=(X⊤X)−1X⊤y.\mathbf{w}^* = (\mathbf X^\top \mathbf X)^{-1}\mathbf X^\top \mathbf{y}.w∗=(X⊤X)−1X⊤y.
随机梯度下降
通常对于训练拟合,可以使用名为梯度下降(gradient descent)的方法,其适用于几乎所有的深度学习模型,
-
其具体方法就是计算算是函数关于模型参数的导数(可以称之为梯度)。但这样执行会很慢(如果样本量很多),因为每次更新参数都要遍历整个(n)数据集。为此,可以随机抽取出一小批样本,这种变形被称之为小批量梯度下降(Minibatch stochastic gradient descent)。
-
每次迭代,随机抽取出小批量数据 B\mathcal{B}B 。之后计算小批量的平均损失关于模型参数的导数。之后将梯度乘以一个预先确定的正数 η\etaη可以称之为学习率(learning rate)。下列式子为更新过程:
(w,b)←(w,b)−η∣B∣∑i∈B∂(w,b)l(i)(w,b).(\mathbf{w},b) \leftarrow (\mathbf{w},b) - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{(\mathbf{w},b)} l^{(i)}(\mathbf{w},b).(w,b)←(w,b)−∣B∣ηi∈B∑∂(w,b)l(i)(w,b). -
故对上述知识进行总结,算法步骤如下:
- 初始化模型参数的值,如随机初始化;
- 数据集中随机抽取小批量样本且在负梯度的方向上更新参数,并不断迭代这一步骤。
对于平方损失和仿射变换,我们可以明确地写成如下形式:
w←w−η∣B∣∑i∈B∂wl(i)(w,b)=w−η∣B∣∑i∈Bx(i)(w⊤x(i)+b−y(i)),b←b−η∣B∣∑i∈B∂bl(i)(w,b)=b−η∣B∣∑i∈B(w⊤x(i)+b−y(i)).\begin{aligned} \mathbf{w} &\leftarrow \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{\mathbf{w}} l^{(i)}(\mathbf{w}, b) = \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right),\\ b &\leftarrow b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_b l^{(i)}(\mathbf{w}, b) = b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right). \end{aligned}wb←w−∣B∣ηi∈B∑∂wl(i)(w,b)=w−∣B∣ηi∈B∑x(i)(w⊤x(i)+b−y(i)),←b−∣B∣ηi∈B∑∂bl(i)(w,b)=b−∣B∣ηi∈B∑(w⊤x(i)+b−y(i)).
当训练达到了预先确定的迭代次数,或者满足某些条件停止后,记录下模型阐述的估计值,表示为 w^\hat{w}w^ 和 b^\hat{b}b^
代码实操
矢量化加速
在训练模型的时候,通常需要对计算样本矢量化进行处理,使用线性代数库,而非使用累赘复杂的for循环进行训练
- 需要的代码库:
特别注明,这里的d2l为李沐老师自己写的代码库,需要自行安装,安装命令如下:
pip install -U d2l
%matplotlib inline
import math
import time
import numpy as np
import torch
from d2l import torch as d2l
若对比矢量计算和for循环计算,可以写一个简单的矩阵加法函数,来进行对比 。
在此实例化两个全为1的10000维向量,分别使用for循环和线性代数库的加法进行时间对比测试:
# 向量定义
n = 10000
a = torch.ones([n])
b = torch.ones([n])# 计时器定义
class Timer: #@save"""记录多次运行时间"""def __init__(self):self.times = []self.start()def start(self):"""启动计时器"""self.tik = time.time()def stop(self):"""停止计时器并将时间记录在列表中"""self.times.append(time.time() - self.tik)return self.times[-1]def avg(self):"""返回平均时间"""return sum(self.times) / len(self.times)def sum(self):"""返回时间总和"""return sum(self.times)def cumsum(self):"""返回累计时间"""return np.array(self.times).cumsum().tolist()
- for循环加法时间计算:
c = torch.zeros(n)
timer = Timer()
for i in range(n):c[i] = a[i] + b[i]
f'{timer.stop():.5f} sec'
Out: ‘0.09227 sec’
- 线性代数库计算:
timer.start()
d = a + b
f'{timer.stop():.5f} sec'
Out:‘0.00103 sec’
不难看出,矢量化代码,会带来指数级别的加速,提高速度的同时,还降低了错误的可能性
正态分布于平方损失
正态分布往往与线性回归之间关系密切,这里通过定义正态分布(normal distribution)来解读平方损失目标函数
- 正态分布定义
def normal(x, mu, sigma):p = 1 / math.sqrt(2 * math.pi * sigma**2)return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)
- 对正态分布进行可视化
# 使用numpy进行可视化
x = np.arange(-7, 7, 0.01)# 均值和标准差对
params = [(0, 1), (0, 2), (3, 1)]
d2l.plot(x, [normal(x, mu, sigma) for mu, sigma in params], xlabel='x',ylabel='p(x)', figsize=(4.5, 2.5),legend=[f'mean {mu}, std {sigma}' for mu, sigma in params])
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qEb232Np-1679495387769)(null)]](/uploadfile/202506/4ed519f3b039.png)
深度网络
神经网络图
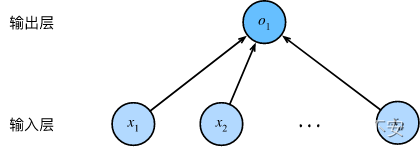
而线性回归则是一个单层神经网络,在上图所示的神经网络中,输入 x1,...,xdx_1,...,x_dx1,...,xd ,因此输入层链接的神经数为d,即为维度特征(feature dimensionaloty)。网络输出为 o1o_1o1 ,即输出维度为1。
对于线性回归,每个输入都与每个输出(在本例中只有一个输出)相连,将这种变换称之为全连接层(fully-connected layer)或者称为稠密层(dense layer)。
