目录

• • 题目链接
  • 题目分析
  • 解题思路
  • • 暴力
    • 中心向两边拓展搜索

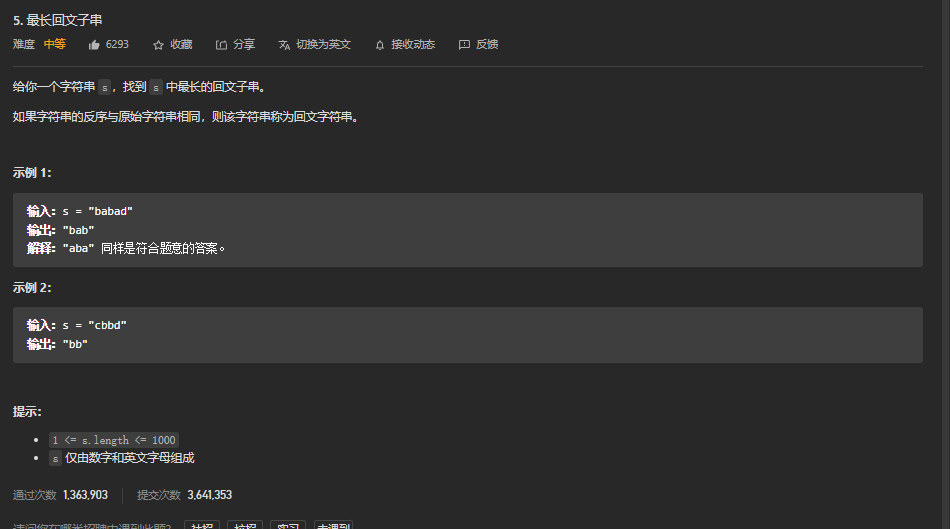
题目链接

链接

题目分析

简单来说，回文串就是正序读和反序读都相同的字符串，回文数类似，比如121 1221 12321都算回文数;

那么明显能看到两种情况:

1. 长度为奇数的回文数: 121 ; 则除了中位数2是单独出现的，其余数字都是对称的！
2. 长度为偶数的回文数: 1221 ; 则以最居中的两个2为基准对称先，其余的数字也是对称的！

解题思路

暴力

刚看完题后，我脑子就想到可以暴力嘛，比如我:

1. 穷举出可能的每种子串;
2. 判断是不是回文串; 是的话记录长度，最终只保留最长的那个返回；

时间复杂度:O(N^3) 穷举字串N^{2，判断是不是回文串为N，嵌套在N}2的循环里;

实现代码

class Solution {
public:bool fun(const string& s)//判断是不是回文串{int len = s.size();int l = 0,r = len-1;while(lif(s[l]!=s[r]) return false;l++;r--;}return true;}string longestPalindrome(string s) {int len = s.size();int max = 0;string tmp;string ret;for(int i = 0;itmp+=s[i];for(int j = i+1;j//双for构造每种字串，临时存入tmp中;tmp+=s[j];if(fun(tmp)){//判断是不是回文串，是的话，如果长度目前是最长，记录到ret中if(tmp.size()>max){max = tmp.size();ret = tmp;}}}tmp.clear();}//! 比如无回文串，abcd，那么就不会记录ret，此时max还是0，这时候特殊处理下，随便聊个字符返回就行(因为此时最长长度为1随便挑一个)!if(max==0) ret = s[0];return ret;}
};

当然，其实临时变量tmp根本不需要，可以勇i和j的下标，以及原始的s串引用的形式传入判断函数中，省一些时间; 不过这个算法本质还是太久了;

中心向两边拓展搜索

暴力的方法太暴力了，虽然能解，但是面试官肯定不会满意的，有没有稍微优雅点的…

观察回文串 aba ; cbabc ; 和 非回文串xcbabcy;

我们发现，对于字符串xcbabcy，我们只需要以a为中心，向两侧拓展类似l r左右双指针的东西就能在bab的基础上得到以a为中心的最大的回文串cbabc！

那么我们一个for循环，便利所有的字符，当作每一个中心，在循环内部while拓展一下，时间复杂度不久控制在了N^2吗！

上面局的例子是总长奇数情况，总长偶数情况我们把i和i+1位当中心就行了，一个道理! 注意while拓展的三种情况，处理好边界就OK

实现代码

class Solution {public:void fun(int& l, int& r, const string& s, const int& len)//扩展
{while (l >= 0 && r < len){if(s[l]!=s[r]) break;//尝试拓展,将两边界扩大1l--;r++;}//不满足while,即尝试拓展失败的时候，代表l+1 到 r-1 其实就是最长回文子串的边界了,处理回去;l++;r--;
}string longestPalindrome(string s) {int len = s.size();int max = 0;//保存最长回文串的长度int ret;//保存最长回文串的起始indexint l;//用于再拓展中带出回文字串的边界，可以计算字串长度和起始indexint r;for (int i = 0; i < len; i++) {//1.假设最长回文子串总长为奇数l = i;r = i;fun(l,r,s,len);if(max//筛选最长max=  r-l+1;ret = l;}//2.假设最长回文子串总长为偶数(中心为i和i+1)l = i;r = i + 1;fun(l,r,s,len);if(max//筛选最长max=  r-l+1;ret = l;}}//一个字符的特殊情况也能处理，不用特殊处理了return s.substr(ret, max);
}
};

代码中需要特别注意的点就是:

1. func拓展函数的设计思想，我们可以尝试拓展，让l–,r++，如果尝试失败，出来的时候，l和r需要恢复到尝试之前,这样设计可以避免繁琐的边界处理条件！比如l就是开头或者r就是结尾等无法拓展的情况; 再一个就是int&l r的设计，很好的能把合法边界带出来!进而计算字串起始位置和长度!
2. 每组"中心"我们需要尝试拓展两次，一次以第i位，一次以i和i+1两位为中心,原因是，可能目前的最长回文子串总长是奇数(中心就是i)，or，总长是偶数(中心就是i,i+1)，得考虑完全!

比如acbbc这个用例，只按照第i位拓展一次的话，那么最长的回文子串长度就是1，当i==2时，按照2，3拓展，才考虑的完全，此时最长回文字串长度为4

可以看到快了很多，当然还有DP等解法，我太菜了就先不研究了!