【视觉高级篇】26 # 如何绘制带宽度的曲线?
创始人
2024-04-24 08:44:33
说明
【跟月影学可视化】学习笔记。
如何用 Canvas2D 绘制带宽度的曲线?
Canvas2D 提供了相应的 API,能够绘制出不同宽度、具有特定连线方式(lineJoin)和线帽形状(lineCap)的曲线,绘制曲线非常简单。
什么是连线方式(lineJoin)?
线宽超过一个像素,两个线段中间转折的部分处就会有缺口,不同的填充方式,就对应了不同的 lineJoin。

线帽形状(lineCap)?
lineCap 就是指曲线头尾部的形状。
- 第一种:
square,方形线帽,它会在线段的头尾端延长线宽的一半。 - 第二种:
round,圆弧线帽,它会在头尾端延长一个半圆。 - 第三种:
butt,不添加线帽。
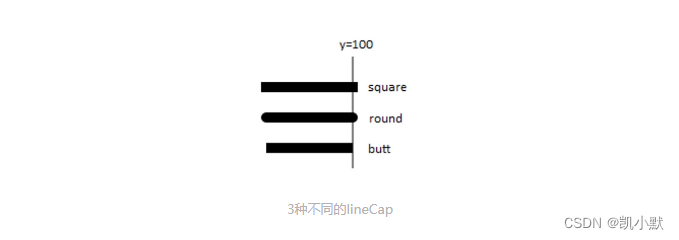
绘制曲线例子
注意:Canvas2D 的 lineJoin 只支持 miter、bevel 和 round,不支持 none。lineCap 支持 butt、square 和 round。
如何用 Canvas2D 绘制带宽度的曲线
效果如下:图三中,两侧的转角由于超过了 miterLimit 限制,所以表现为斜角,而中间的转角因为没有超过 miterLimit 限制,所以是尖角。
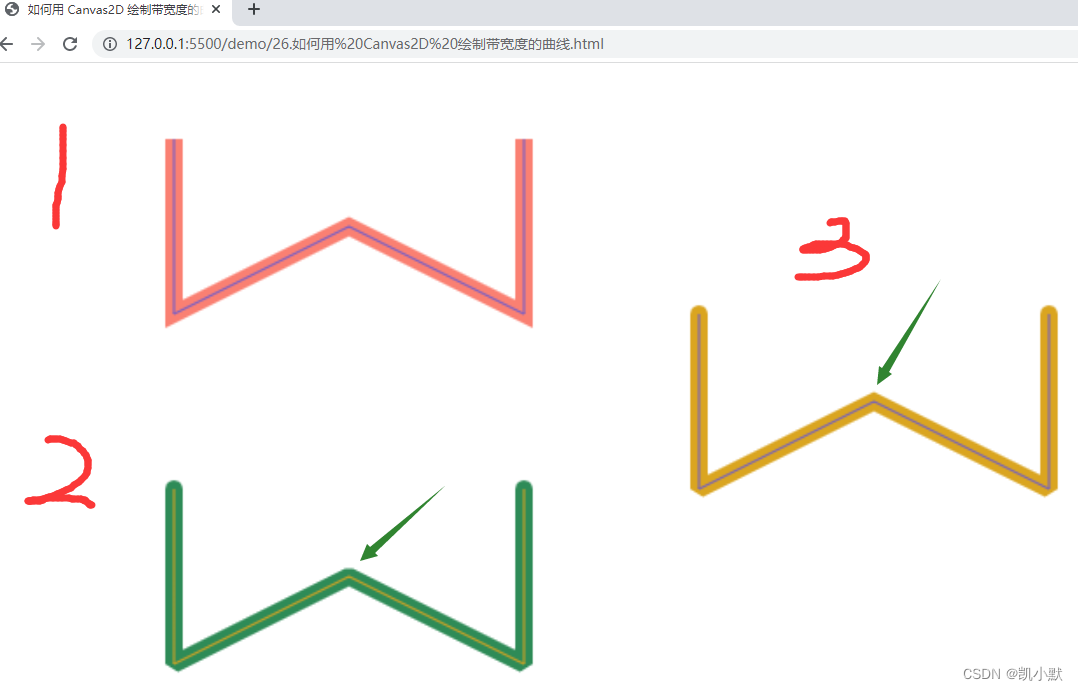
如何用 WebGL 绘制带宽度的曲线
WebGL 支持线段类的图元,LINE_STRIP 是一种图元类型,表示以首尾连接的线段方式绘制。
用 WebGL 绘制宽度为 1 的曲线
用 WebGL 绘制宽度为 1 的曲线
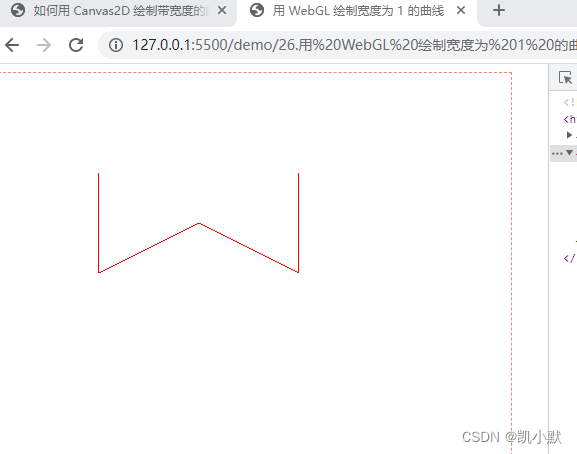
通过挤压 (extrude) 曲线绘制有宽度的曲线
挤压 (extrude) 曲线就是将曲线的顶点沿法线方向向两侧移出,让 1 个像素的曲线变宽。
大致步骤:
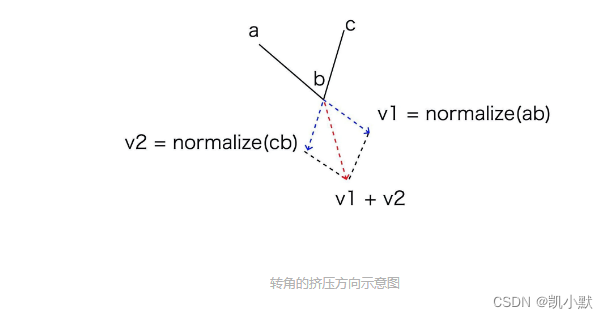
- 1、确定端点和转角的挤压方向,端点可以沿线段的法线挤压,转角则通过两条线段延长线的单位向量求和的方式获得。
- 2、确定端点和转角挤压的长度
- 端点两个方向的挤压长度是线宽 lineWidth 的一半。
- 求转角挤压长度的时候,要先计算方向向量和线段法线的余弦,然后将线宽 lineWidth 的一半除以我们计算出的余弦值。
- 3、由步骤 1、2 计算出顶点后,我们构建三角网格化的几何体顶点数据,然后将 Geometry 对象返回。
如下图所示:
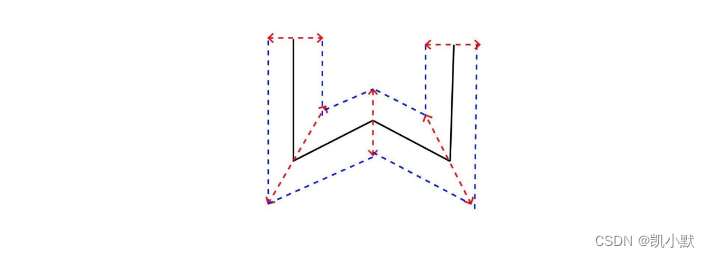
折线端点的挤压方向
顶点的两个移动方向为(-y, x)和(y, -x)。
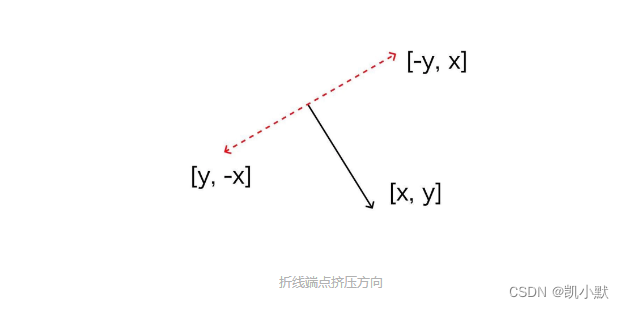
转角的挤压方向
折线端点的挤压长度
折线端点的挤压长度等于 lineWidth 的一半。
转角的挤压长度
需要计算法线方向与挤压方向的余弦值,就能算出挤压长度
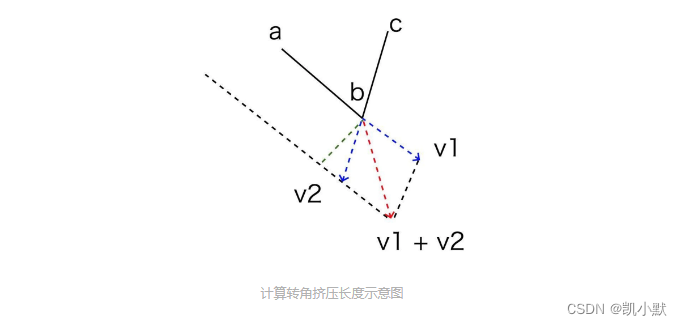
用 JavaScript 实现的代码如下所示:
function extrudePolyline(gl, points, {thickness = 10} = {}) {const halfThick = 0.5 * thickness;// 向内和向外挤压的点分别保存在 innerSide 和 outerSide 数组中。const innerSide = [];const outerSide = [];// 构建挤压顶点for(let i = 1; i < points.length - 1; i++) {// v1、v2 是线段的延长线,v 是挤压方向const v1 = (new Vec2()).sub(points[i], points[i - 1]).normalize();const v2 = (new Vec2()).sub(points[i], points[i + 1]).normalize();const v = (new Vec2()).add(v1, v2).normalize(); // 得到挤压方向const norm = new Vec2(-v1.y, v1.x); // 法线方向const cos = norm.dot(v);const len = halfThick / cos;if(i === 1) { // 起始点const v0 = new Vec2(...norm).scale(halfThick);outerSide.push((new Vec2()).add(points[0], v0));innerSide.push((new Vec2()).sub(points[0], v0));}v.scale(len);outerSide.push((new Vec2()).add(points[i], v));innerSide.push((new Vec2()).sub(points[i], v));if(i === points.length - 2) { // 结束点const norm2 = new Vec2(v2.y, -v2.x);const v0 = new Vec2(...norm2).scale(halfThick);outerSide.push((new Vec2()).add(points[points.length - 1], v0));innerSide.push((new Vec2()).sub(points[points.length - 1], v0));}}const count = innerSide.length * 4 - 4;const position = new Float32Array(count * 2);const index = new Uint16Array(6 * count / 4);// 创建 geometry 对象for(let i = 0; i < innerSide.length - 1; i++) {const a = innerSide[i],b = outerSide[i],c = innerSide[i + 1],d = outerSide[i + 1];const offset = i * 4;index.set([offset, offset + 1, offset + 2, offset + 2, offset + 1, offset + 3], i * 6);position.set([...a, ...b, ...c, ...d], i * 8);}return new Geometry(gl, {position: {size: 2, data: position},index: {data: index},});
}
根据 innerSide 和 outerSide 中的顶点来构建三角网格化的几何体顶点数据,最终返回 Geometry 对象来构建三角网格对象。
构建折线的顶点数据示意图:
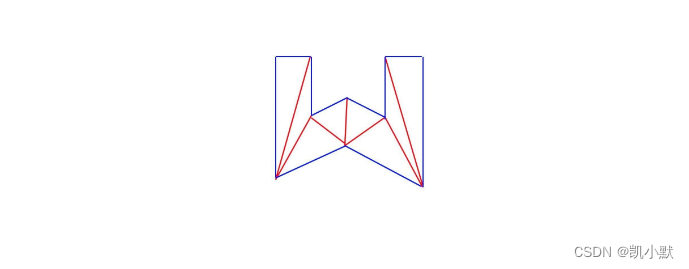
下面实战一下:
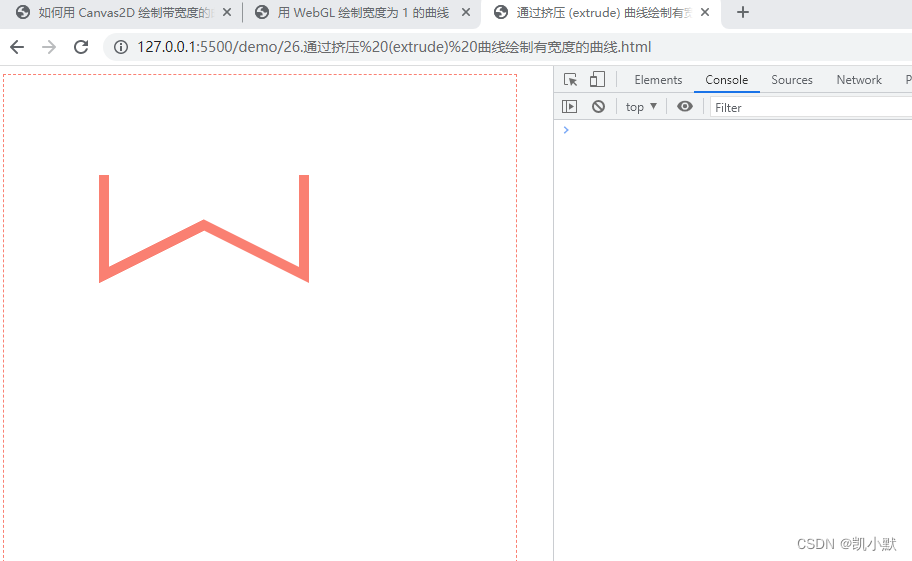
通过挤压 (extrude) 曲线绘制有宽度的曲线
参考资料
- Cartographical Symbol Construction with MapServer
下一篇:餐饮后台管理系统
相关内容
热门资讯
demo什么意思 demo版本...
618快到了,各位的小金库大概也在准备开闸放水了吧。没有小金库的,也该向老婆撒娇卖萌服个软了,一切只...
苗族的传统节日 贵州苗族节日有...
【岜沙苗族芦笙节】岜沙,苗语叫“分送”,距从江县城7.5公里,是世界上最崇拜树木并以树为神的枪手部落...
北京的名胜古迹 北京最著名的景...
北京从元代开始,逐渐走上帝国首都的道路,先是成为大辽朝五大首都之一的南京城,随着金灭辽,金代从海陵王...
