【矩阵论】6. 范数理论——基本概念——向量范数与矩阵范数
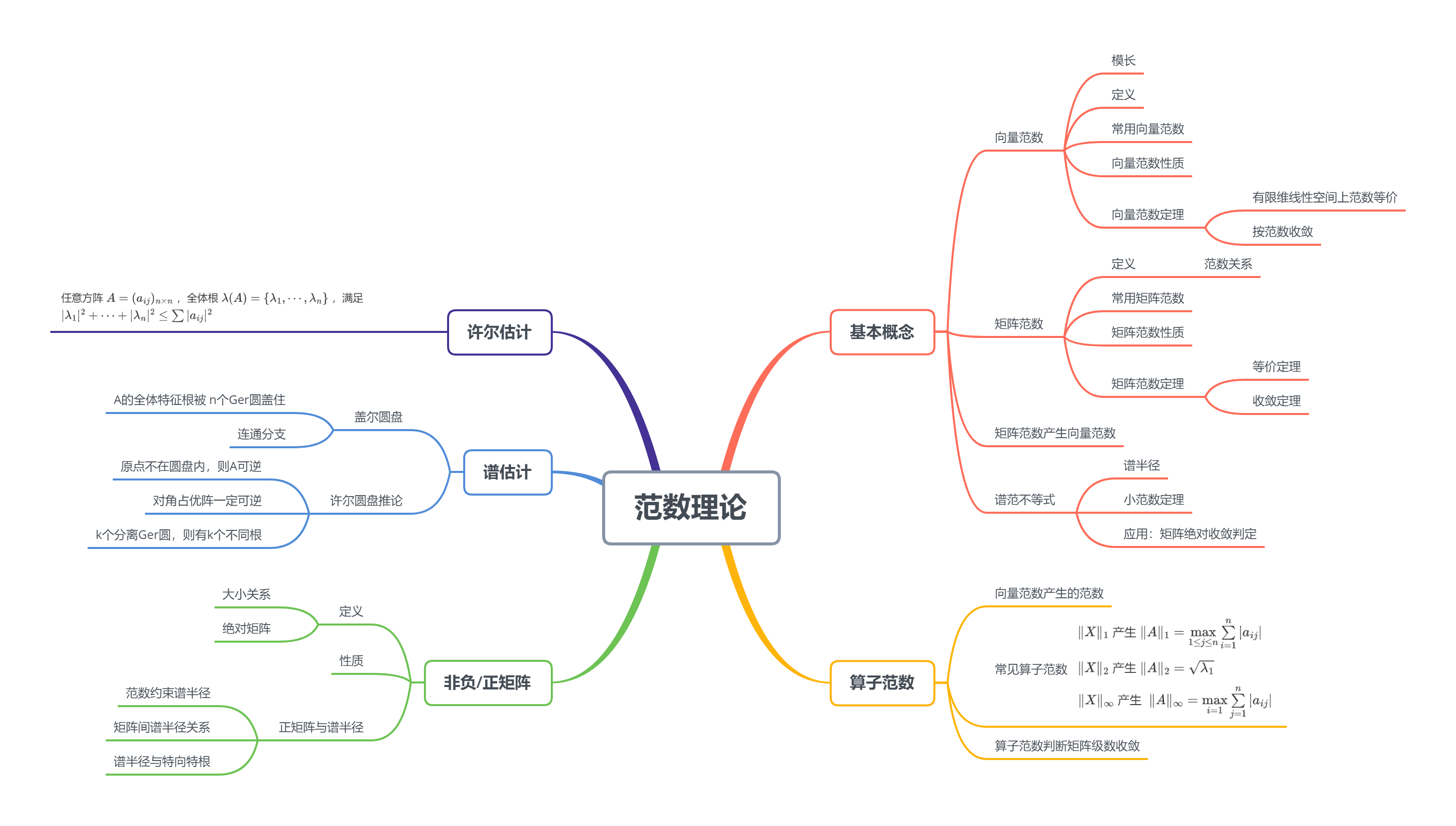
6.1 基本概念
6.1.1 向量范数
a. 模长(二范数)
Cn中向量X=(x1x2⋮xn)的模长为∣X∣=(X,X)=tr(AHA)=∣x1∣2+∣x2∣2+⋯+∣xn∣2C^n中向量 X=\left( \begin{matrix} x_1\\x_2\\\vdots\\x_n \end{matrix} \right)的模长为 \vert X\vert=\sqrt{(X,X)}=\sqrt{tr(A^HA)} =\sqrt{\vert x_1\vert^2+\vert x_2\vert^2+\cdots+\vert x_n\vert^2 } Cn中向量X=x1x2⋮xn的模长为∣X∣=(X,X)=tr(AHA)=∣x1∣2+∣x2∣2+⋯+∣xn∣2
-
正性:∣X∣>0\vert X\vert>0∣X∣>0
-
齐性:∣kX∣=∣k∣∣X∣\vert kX\vert=\vert k\vert \vert X\vert∣kX∣=∣k∣∣X∣
∣−x∣=∣x∣\vert -x\vert=\vert x\vert∣−x∣=∣x∣
-
三角性:∣x+y∣≤∣x∣+∣y∣\vert x+y\vert\le \vert x\vert +\vert y\vert∣x+y∣≤∣x∣+∣y∣
∣∣x∣−∣y∣∣≤∣x−y∣\left| \vert x\vert-\vert y\vert \right|\le \vert x-y\vert∣∣x∣−∣y∣∣≤∣x−y∣
内积空间引入模长
任一内积空间W都可引入向量z长度(模长) ∣α∣=(α,α),α∈W\vert \alpha\vert=\sqrt{(\alpha,\alpha)},\alpha\in W∣α∣=(α,α),α∈W
满足柯西-施瓦茨不等式 ∣α+β∣≤(α,α)(β,β)=∣α∣∣β∣\vert \alpha+\beta\vert\le \sqrt{(\alpha,\alpha)}\sqrt{(\beta,\beta)}=\vert \alpha\vert\vert \beta\vert∣α+β∣≤(α,α)(β,β)=∣α∣∣β∣
- 三角性:∣α+β∣≤∣α∣+∣β∣\vert \alpha+\beta\vert \le \vert \alpha\vert+\vert \beta\vert∣α+β∣≤∣α∣+∣β∣
- 正性
- 齐性
二维空间引入模长范数
令矩阵空间 V=Cm,nV=C^{m,n}V=Cm,n ,A=(aij),B=(bij)∈Cm,nA=(a_{ij}),B=(b_{ij})\in C^{m,n}A=(aij),B=(bij)∈Cm,n ,
(A,B)=BHA=tr(BHA)=tr(AHB)=∑(∣aij∣∣bij∣‾)(A,B)=B^HA=tr(B^HA)=tr(A^HB)=\sum(\vert a_{ij}\vert\overline{\vert b_{ij}\vert}) (A,B)=BHA=tr(BHA)=tr(AHB)=∑(∣aij∣∣bij∣)
规定 ∥A∥=(A,A)=tr(AHA)=tr(AAH)=∑∣aij∣2\Vert A\Vert=\sqrt{(A,A)}=\sqrt{tr(A^HA)}=\sqrt{tr(AA^H)}=\sqrt{\sum \vert a_{ij}\vert^2}∥A∥=(A,A)=tr(AHA)=tr(AAH)=∑∣aij∣2 为A的F范数
b. 向量范数定义
设 VVV 是数域 FFF (实数域或复数域) 上的线性空间,若对于任一 X∈VX\in VX∈V ,对应一个非负数,记为 ∥X∥\Vert X \Vert∥X∥ 满足以下三个条件,则称 ∥X∥\Vert X\Vert∥X∥ 为空间 V 上的一个向量范数
- 正性:∥X∥>0\Vert X\Vert>0∥X∥>0
- 齐次性: ∥kX∥=∣k∣∥X∥\Vert kX\Vert=\vert k\vert\Vert X\Vert∥kX∥=∣k∣∥X∥
- 三角不等式:∥X+Y∥≤∥X∥+∥Y∥\Vert X+Y\Vert\le \Vert X\Vert+\Vert Y\Vert∥X+Y∥≤∥X∥+∥Y∥
相当于规定在空间V上的一个非负函数 φ(x)=∥x∥,x∈V\varphi(x)=\Vert x\Vert,x\in Vφ(x)=∥x∥,x∈V ,满足正性,齐性,三角性
可知 CnC^nCn 上有很多(无穷) 个范数
范数定义2:若线性空间 VVV 上有一个函数 φ(x),x∈V\varphi(x),x\in Vφ(x),x∈V 适合
- 正性:φ(x)>0,x≠0⃗\varphi(x)>0,x\neq \vec{0}φ(x)>0,x=0
- 齐性:φ(kx)=∣k∣φ(x),x∈V\varphi(kx)=\vert k\vert\varphi(x),x\in Vφ(kx)=∣k∣φ(x),x∈V
- 三角形:φ(x+y)≤φ(x)+φ(y)\varphi(x+y)\le \varphi(x)+\varphi(y)φ(x+y)≤φ(x)+φ(y)
则称 φ(x)\varphi(x)φ(x) 为 VVV 上的一个范数,记为 φ(x)=∥x∥\varphi(x)=\Vert x\Vertφ(x)=∥x∥
eg:
验证给定函数是否为范数

∵A>0,则由平方根公式A=B2=BHB⇒XHAX=XHBHBX=∣BX∣2⇒∥x∥=∣BX∣2=∥BX∥2>0,且满足齐性∥x+y∥=∥B(x+y)∥2=∥Bx+By∥2≤∥Bx∥2+∥By∥2=∥x∥+∥y∥,满足三角性\begin{aligned} &\because A>0,则由平方根公式A=B^2=B^HB\Rightarrow X^HAX=X^HB^HBX=\vert BX\vert^2\\ &\Rightarrow \Vert x\Vert=\sqrt{\vert BX\vert^2}= \Vert BX\Vert_2>0,且满足齐性\\ &\Vert x+y\Vert=\Vert B(x+y)\Vert_2=\Vert Bx+By\Vert_2\le \Vert Bx\Vert_2+\Vert By\Vert_2=\Vert x\Vert+\Vert y\Vert ,满足三角性 \end{aligned} ∵A>0,则由平方根公式A=B2=BHB⇒XHAX=XHBHBX=∣BX∣2⇒∥x∥=∣BX∣2=∥BX∥2>0,且满足齐性∥x+y∥=∥B(x+y)∥2=∥Bx+By∥2≤∥Bx∥2+∥By∥2=∥x∥+∥y∥,满足三角性
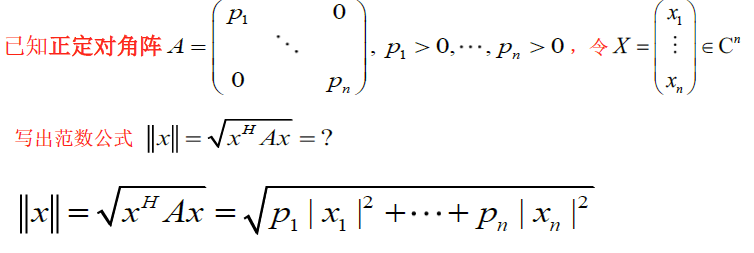
c. 复向量空间中常用范数
1-范数:∥x∥1=∑(∣x1∣+⋯+∣xn∣)\Vert x\Vert_1=\sum(\vert x_1\vert+\cdots+\vert x_n\vert)∥x∥1=∑(∣x1∣+⋯+∣xn∣)
2-范数:∥x∥2=(x,x)=∣x1∣2+⋯+∣xn∣2\Vert x\Vert_2=\sqrt{(x,x)}=\sqrt{\vert x_1\vert^2+\cdots+\vert x_n\vert^2}∥x∥2=(x,x)=∣x1∣2+⋯+∣xn∣2
∞\infty∞-范数:∥x∥∞=max{∣x1∣,⋯,∣xn∣}\Vert x\Vert_{\infty}=max\{\vert x_1\vert,\cdots,\vert x_n\vert\}∥x∥∞=max{∣x1∣,⋯,∣xn∣}
p-范数:∥x∥p=(∑i=1n∣xi∣2)12,p≥1\Vert x\Vert_p=\left(\sum_{i=1}\limits^{n}\vert x_i\vert^2\right)^{\frac{1}{2}} ,p\ge 1∥x∥p=(i=1∑n∣xi∣2)21,p≥1
d. 向量范数性质
单位化公式:X≠0X\neq 0X=0 ,则 X∥X∥\frac{X}{\Vert X\Vert}∥X∥X 是范数为1的向量
∥−X∥=∥X∥\Vert -X\Vert=\Vert X\Vert∥−X∥=∥X∥
∥X−Y∥≥∣∥X∥−∥Y∥∣\Vert X-Y\Vert\ge \vert\Vert X\Vert-\Vert Y\Vert \vert∥X−Y∥≥∣∥X∥−∥Y∥∣
e. 有限维线性空间上范数等价性
对于 CnC^nCn 上任两个范数 ∥X∥a\Vert X\Vert_a∥X∥a ,∥X∥b\Vert X\Vert_b∥X∥b 存在正数:k1>0,k2>0k_1>0,k_2>0k1>0,k2>0 ,使 k1∥X∥b<∥X∥a 证明 设 CnC^nCn 中向量序列:X(k)=(X1(k),X2(k),⋯,,Xn(k))X^{(k)}=\left(X_1^{(k)},X_2^{(k)},\cdots,,X_n^{(k)}\right)X(k)=(X1(k),X2(k),⋯,,Xn(k)) (k=1,2,⋯k=1,2,\cdotsk=1,2,⋯) ,α=(α1,α2,⋯,αn)T\alpha=\left(\alpha_1,\alpha_2,\cdots,\alpha_n\right)^Tα=(α1,α2,⋯,αn)T ,若 X1(k)→α1X_1^{(k)}\rightarrow\alpha_1X1(k)→α1 ,X2(k)→α2X_2^{(k)}\rightarrow\alpha_2X2(k)→α2 ,⋯\cdots⋯ ,Xn(k)→αnX_n^{(k)}\rightarrow\alpha_nXn(k)→αn (k→∞k\rightarrow \inftyk→∞),则称 X(k)→αX^{(k)}\rightarrow\alphaX(k)→α ,或 limX(k)=α\lim X^{(k)}=\alphalimX(k)=α 设 X1,⋯,Xm,⋯X_1,\cdots,X_m,\cdotsX1,⋯,Xm,⋯ 是线性空间V中的元素序列,若 X0∈VX_0\in VX0∈V ,使 limm→∞∥Xm−X0∥α=0\lim_{m\rightarrow\infty}\limits \Vert X_m-X_0\Vert_\alpha=0m→∞lim∥Xm−X0∥α=0 ,称序列 {Xm}\{X_m\}{Xm} 按范数 ∥∙∥α\Vert \bullet \Vert_\alpha∥∙∥α 收敛于 X0X_0X0 ,记为 limm→∞Xm=αX0\lim_{m\rightarrow\infty}\limits X_m\xlongequal{\alpha}X_0m→∞limXmαX0 若序列 {Xm}\{X_m \}{Xm} 按某一范数收敛于 X0X_0X0 ,则 {Xm}\{X_m\}{Xm} 按任何范数都收敛于 X0X_0X0 ,即有限维空间按范数收敛是互相等价的 序列 {Xm}\{X_m\}{Xm} 按范数收敛于 X0X_0X0 ⟺\iff⟺ 按坐标收敛于 X0X_0X0 对于一个方阵 A∈Cn,nA\in C^{n,n}A∈Cn,n ,矩阵范数 ∥A∥\Vert A\Vert∥A∥ 表示某个法则与A对应的非负函数,且满足4个条件: 则 ∥A∥\Vert A\Vert∥A∥ 为矩阵范数(相容范数) 矩阵范数定义2:设方阵空间 Cn×nC^{n\times n}Cn×n 上非负函数 φ(A),A∈Cn×n\varphi(A),A\in C^{n\times n}φ(A),A∈Cn×n ,有: 则称 φ(A)\varphi(A)φ(A) 为空间 Cn×nC^{n\times n}Cn×n 上的矩阵范数,记为 φ(A)=∥A∥\varphi(A)=\Vert A\Vertφ(A)=∥A∥ 令方阵 A=(aij)n×n∈Cn×nA=(a_{ij})_{n\times n} \in C^{n\times n}A=(aij)n×n∈Cn×n 1-范数(最大列和):∥A∥1=maxj∑i=1n∣aij∣,j=1,⋯,n\Vert A\Vert_1=\max_j\limits \sum_{i=1}\limits^n\vert a_{ij}\vert ,j=1,\cdots,n∥A∥1=jmaxi=1∑n∣aij∣,j=1,⋯,n 列是一个数据,对应的是向量范数的1-范数,能代表一个列向量 ∞\infty∞ 范数(最大行和):∥A∥∞=maxi∑j=1n∣aij∣(i=1,⋯,n)\Vert A\Vert_{\infty}=\max_i\limits\sum_{j=1}\limits^n\vert a_{ij} \vert(i=1,\cdots,n)∥A∥∞=imaxj=1∑n∣aij∣(i=1,⋯,n) 行是一个维度,对应的是向量范数的 ∞\infty∞ -范数,能代表一个维度特征 2-范数(谱范数):∥A∥2=(λ1(AHA))12\Vert A\Vert_2 =(\lambda_1(A^HA))^\frac{1}{2}∥A∥2=(λ1(AHA))21 ,λ1(AHA)\lambda_1(A^HA)λ1(AHA) 表示 AHAA^HAAHA 的最大特征值,即 ∥A∥2\Vert A\Vert_2∥A∥2 是 A 的最大特征值 总和范数:∥A∥M=∑∣aij∣\Vert A\Vert_M=\sum\vert a_{ij}\vert∥A∥M=∑∣aij∣ F-范数:∥A∥F=(∑∣aij∣2)12=tr(AHA)\Vert A\Vert_F=(\sum \vert a_{ij}\vert^2)^\frac{1}{2}=\sqrt{tr(A^HA)}∥A∥F=(∑∣aij∣2)21=tr(AHA) G-范数:∥A∥G=n⋅max{∣aij∣}\Vert A\Vert_G=n\cdot max\{\vert a_{ij}\vert\}∥A∥G=n⋅max{∣aij∣} eg ∥A∥∞=∥AH∥1,∥A∥1=∥AH∥∞∥A∥2=∥AH∥2,∥A∥F=∥AH∥F=(tr(AHA))12U,V为U阵,则∥UA∥F=∥AV∥F=∥UAV∥F=∥A∥FA∈Cn×n,x∈Cn,则∥Ax∥2≤∥A∥F∥x∥2\begin{aligned} &\Vert A\Vert_{\infty}=\Vert A^H\Vert_1,\Vert A\Vert_1=\Vert A^H\Vert_\infty\\ &\Vert A\Vert_2=\Vert A^H\Vert_2,\Vert A\Vert_F=\Vert A^H\Vert_F=(tr(A^HA))^{\frac{1}{2}}\\ &U,V为U阵,则 \Vert UA\Vert_F=\Vert AV\Vert_F=\Vert UAV\Vert_F=\Vert A\Vert_F\\ &A\in C^{n\times n},x\in C^n,则 \Vert Ax\Vert_2\le \Vert A\Vert_F\Vert x\Vert_2 \end{aligned} ∥A∥∞=∥AH∥1,∥A∥1=∥AH∥∞∥A∥2=∥AH∥2,∥A∥F=∥AH∥F=(tr(AHA))21U,V为U阵,则∥UA∥F=∥AV∥F=∥UAV∥F=∥A∥FA∈Cn×n,x∈Cn,则∥Ax∥2≤∥A∥F∥x∥2 ∥A±B∥≤∥A∥+∥B∥\Vert A\pm B\Vert\le \Vert A\Vert+\Vert B\Vert∥A±B∥≤∥A∥+∥B∥ ∥AB∥≤∥A∥⋅∥B∥\Vert AB\Vert \le \Vert A\Vert\cdot \Vert B\Vert∥AB∥≤∥A∥⋅∥B∥ 幂公式:∥Ak∥≤∥A∥k\Vert A^k\Vert\le \Vert A\Vert^k∥Ak∥≤∥A∥k ∥I∥≥1\Vert I\Vert\ge 1∥I∥≥1 谱半径幂公式:ρ(Ak)≤[ρ(A)]k\rho(A^k)\le [\rho(A)]^kρ(Ak)≤[ρ(A)]k ,k=1,2,… 公式:∥kA∥=∣k∣⋅∥A∥\Vert kA\Vert=\vert k\vert\cdot\Vert A\Vert∥kA∥=∣k∣⋅∥A∥ ,ρ(kA)=∣k∣ρ(A)\rho(kA)=\vert k\vert\rho(A)ρ(kA)=∣k∣ρ(A) SP:∥−A∥=∥A∥\Vert -A\Vert=\Vert A\Vert∥−A∥=∥A∥ ,ρ(−A)=ρ(A)\rho(-A)=\rho(A)ρ(−A)=ρ(A) SP : 任一矩阵范数 ∥A∥\Vert A\Vert∥A∥ 都和总和范数 ∥A∥M=∑∣ai,j∣\Vert A\Vert_M=\sum\vert a_{i,j}\vert∥A∥M=∑∣ai,j∣ 等价,存在整数 k1k_1k1,k2k_2k2 ,使 k1≤∥A∥∥A∥M≤k2k_1\le \frac{\Vert A\Vert}{\Vert A\Vert_M}\le k_2k1≤∥A∥M∥A∥≤k2 1n≤∥A∥1∥A∥M≤1\frac{1}{n}\le \frac{\Vert A\Vert_1}{\Vert A\Vert_M}\le 1n1≤∥A∥M∥A∥1≤1 ,1n≤∥A∥∞∥A∥M≤1\frac{1}{n}\le \frac{\Vert A\Vert_\infty}{\Vert A\Vert_M}\le 1n1≤∥A∥M∥A∥∞≤1 ,1n≤∥A∥F∥A∥M≤1\frac{1}{n}\le \frac{\Vert A\Vert_F}{\Vert A\Vert_M}\le 1n1≤∥A∥M∥A∥F≤1
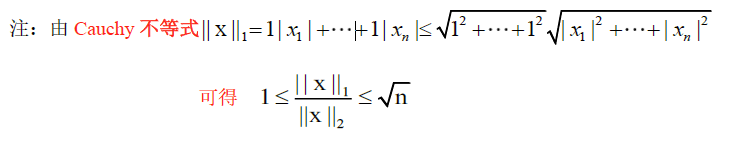

f. 范数收敛定理
收敛定义
X(k)→α⟺∥X(k)−α∥→0X^{(k)}\rightarrow \alpha\iff \Vert X^{(k)}-\alpha\Vert\rightarrow 0 X(k)→α⟺∥X(k)−α∥→0按范数收敛

取一组基底e1,e2,⋯,en,令Xm=ξ1(m)e1+⋯+ξn(m)en,X0=ξ1(0)e1+⋯+ξn(0)en由二范数定义,∀x=(ξ1ξ2⋮ξn)∈Cn,∥X∥2=(∑i=1n∣ξi∣2)12按范数收敛是等价的,∴limm→∞∥Xm−X0∥=0⟺limm→∞∥Xm−X0∥2=0⟺limm→∞(∑i=1n∣ξi(m)−ξi(0)∣2)⟺limm→∞ξi(m)=ξi(0)\begin{aligned} &取一组基底e_1,e_2,\cdots,e_n,令X_m=\xi_1^{(m)}e_1+\cdots+\xi_n^{(m)}e_n,X_0=\xi_1^{(0)}e_1+\cdots+\xi_n^{(0)}e_n\\ &由二范数定义,\forall x=\left( \begin{matrix} \xi_1\\\xi_2\\\vdots\\\xi_n \end{matrix} \right)\in C^n,\Vert X\Vert_2=(\sum_{i=1}\limits^n\vert \xi_i\vert^2)^{\frac{1}{2}}\\ &按范数收敛是等价的,\therefore\lim_{m\rightarrow \infty}\Vert X_m-X_0\Vert=0\iff \lim_{m\rightarrow \infty}\Vert X_m-X_0\Vert_2=0\\ &\iff \lim_{m\rightarrow \infty}(\sum_{i=1}\limits^n\vert \xi_i^{(m)}-\xi_i^{(0)}\vert^2 )\iff \lim_{m\rightarrow \infty}\xi_i^{(m)}=\xi_i^{(0)} \end{aligned} 取一组基底e1,e2,⋯,en,令Xm=ξ1(m)e1+⋯+ξn(m)en,X0=ξ1(0)e1+⋯+ξn(0)en由二范数定义,∀x=ξ1ξ2⋮ξn∈Cn,∥X∥2=(i=1∑n∣ξi∣2)21按范数收敛是等价的,∴m→∞lim∥Xm−X0∥=0⟺m→∞lim∥Xm−X0∥2=0⟺m→∞lim(i=1∑n∣ξi(m)−ξi(0)∣2)⟺m→∞limξi(m)=ξi(0)6.1.2 矩阵范数
a. 矩阵范数定义
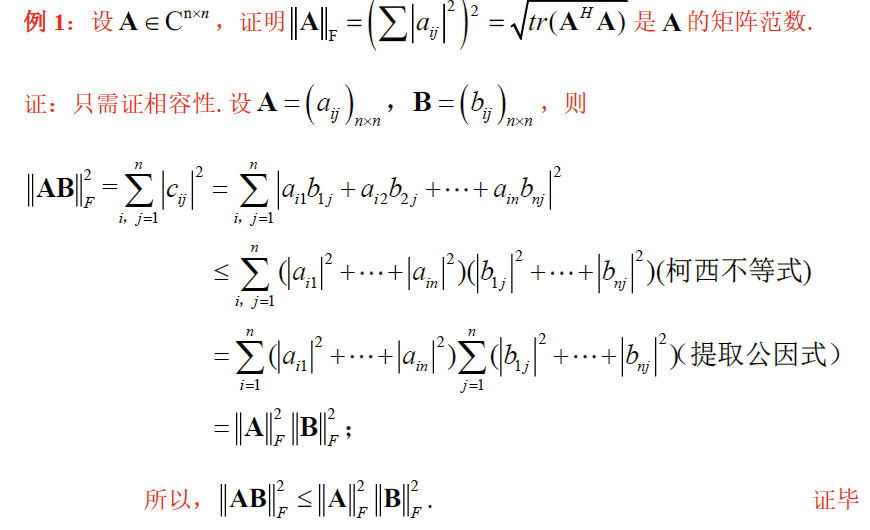
b. 常用范数
几种范数关系
c. 矩阵范数性质
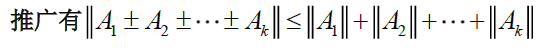
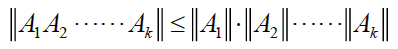
由谱半径定义ρ(A)=max{∣λ1∣,∣λ2∣,⋯,∣λn∣},其中方阵A=An×n特征值λ(A)={λ1,⋯,λn}可知λ(Ak)={λ1k,⋯,λnk}⇒ρ(Ak)=max{∣λ1∣k,⋯,∣λn∣k}=[ρ(A)]k\begin{aligned} &由谱半径定义 \rho(A)=max\{\vert \lambda_1\vert,\vert \lambda_2\vert,\cdots,\vert \lambda_n\vert\},\\ &其中方阵A=A_{n\times n} 特征值\lambda(A)=\{\lambda_1,\cdots,\lambda_n\}\\ &可知 \lambda(A^k)=\{\lambda_1^k,\cdots,\lambda_n^k\}\Rightarrow \rho(A^k)=max\{\vert \lambda_1\vert^k,\cdots,\vert \lambda_n\vert^k \}=[\rho(A)]^k \end{aligned} 由谱半径定义ρ(A)=max{∣λ1∣,∣λ2∣,⋯,∣λn∣},其中方阵A=An×n特征值λ(A)={λ1,⋯,λn}可知λ(Ak)={λ1k,⋯,λnk}⇒ρ(Ak)=max{∣λ1∣k,⋯,∣λn∣k}=[ρ(A)]kd. 矩阵范数定理
