引入

对一个数组进行操作，可以对某个下标位置增加或者减少，也可以对某一区域进行增加或者减少。最朴素的方式就是暴力，但是当数据过大的时候必然会T。这个时候就可以用到树状数组。树状数组形如其名，结构图像树，但是又和树不一样。他没有线段树那么拓展性高，很多线段树能做但是她不能做，但是他也有优点，如果一个题目线段树和树状数组都能用的时候，那么树状数组是明显比线段树快的（还没学线段树，但是听大佬都是这么说的）先把坑挖好

树状数组介绍

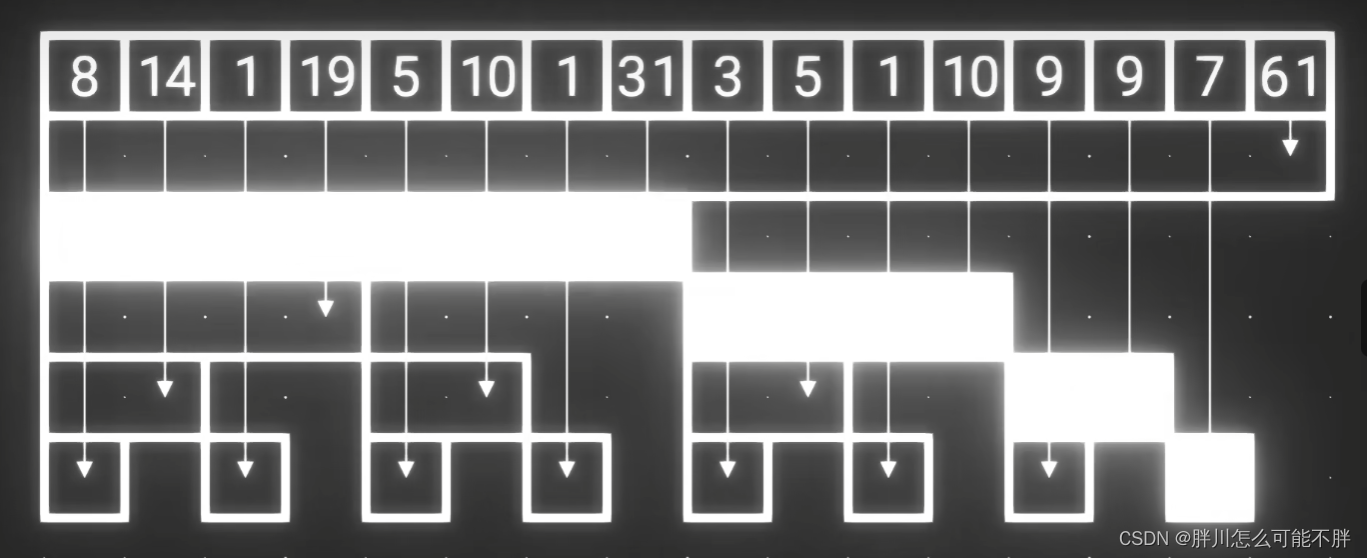
树状数组里面运用了前缀和的思想，先看图

把数字俩俩求和，这样修改数据就会减少一半的时间

那既然都想到求和了，那么为什么不多求几次和呢？

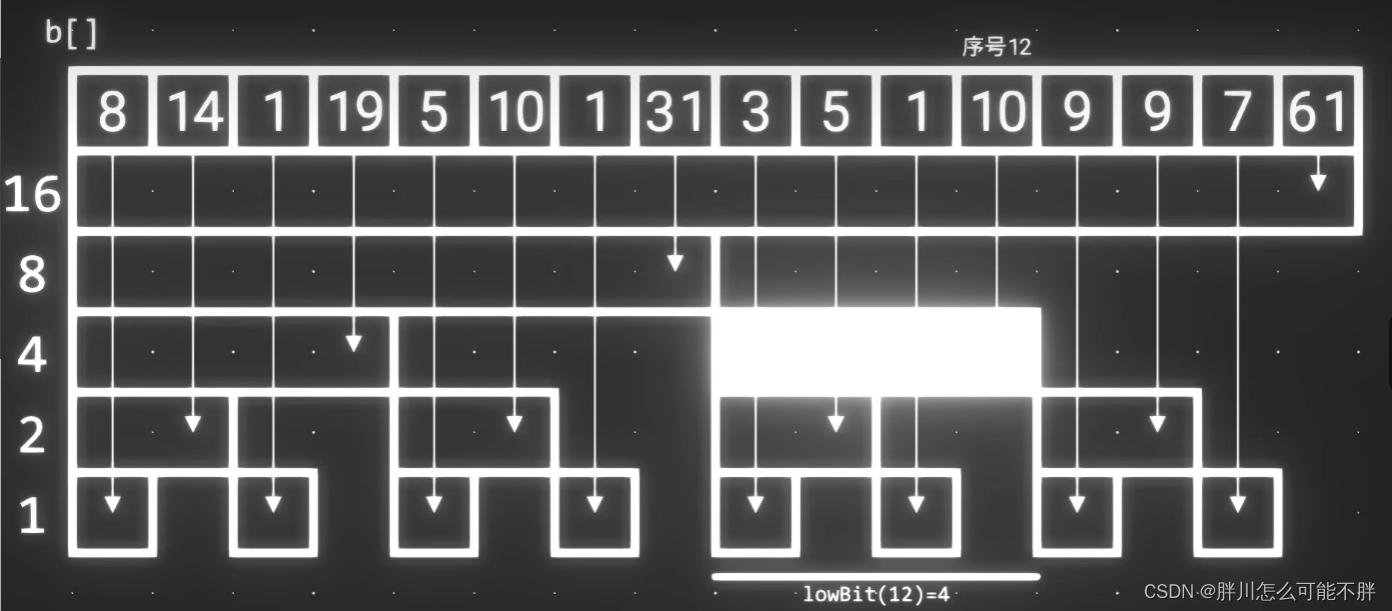
这样的话，即使计算几百万个数的和，也只要计算十几二十次，大大减少了TLE的可能性

但是不难发现，其实这个表格当中是由好多的数据是不用的比如5：

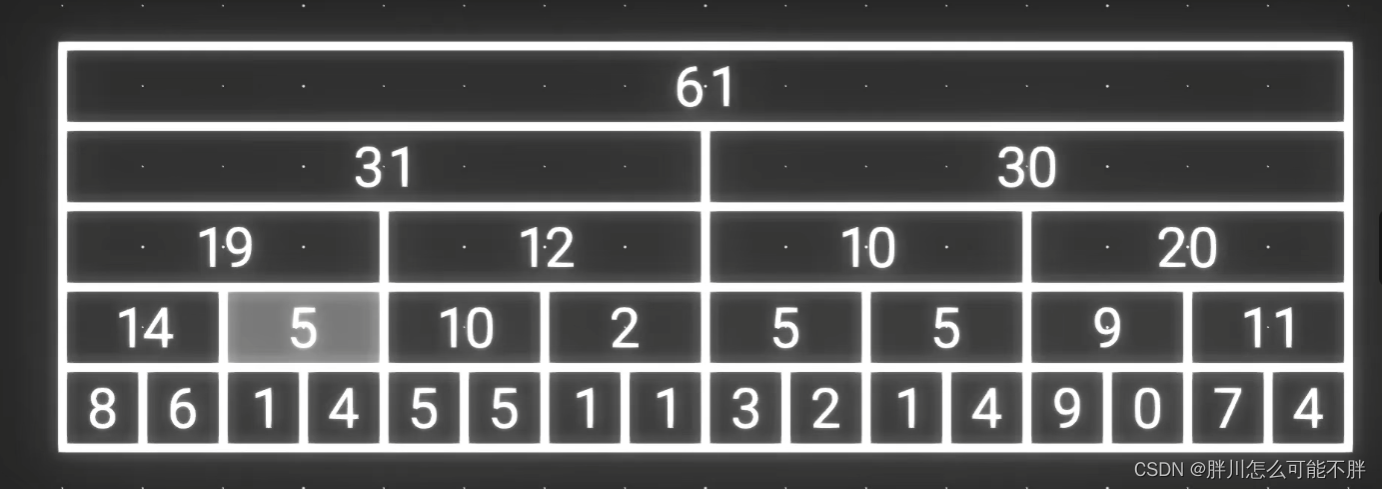
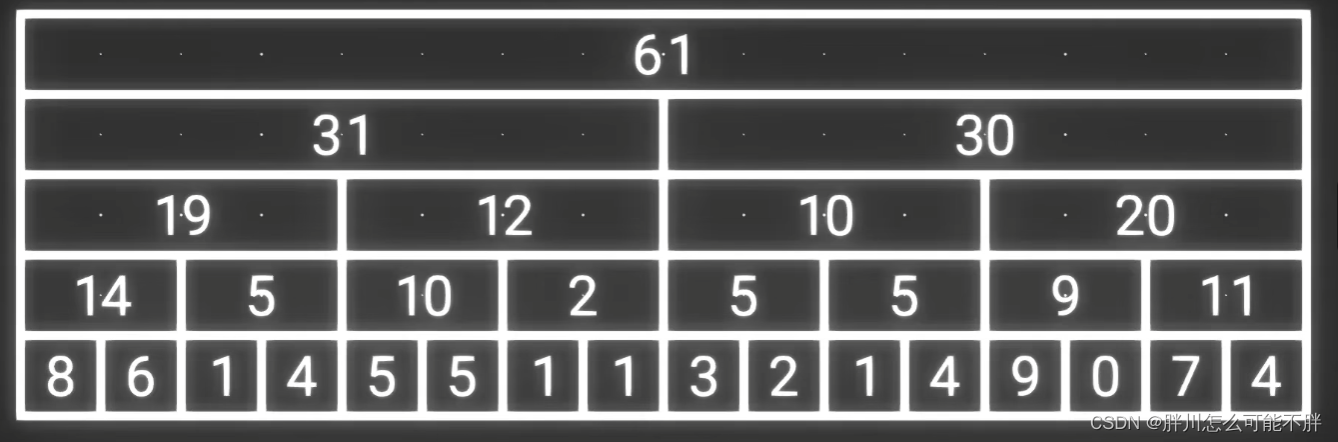
那么就将这些用不到的数字都删除掉，几乎所有层的第偶数个数字都是没用的，那么删掉之后就会得到如下情况

这么一来将他们平移上去刚好是n个数据，放到一个数组里面，那就是树状数组了

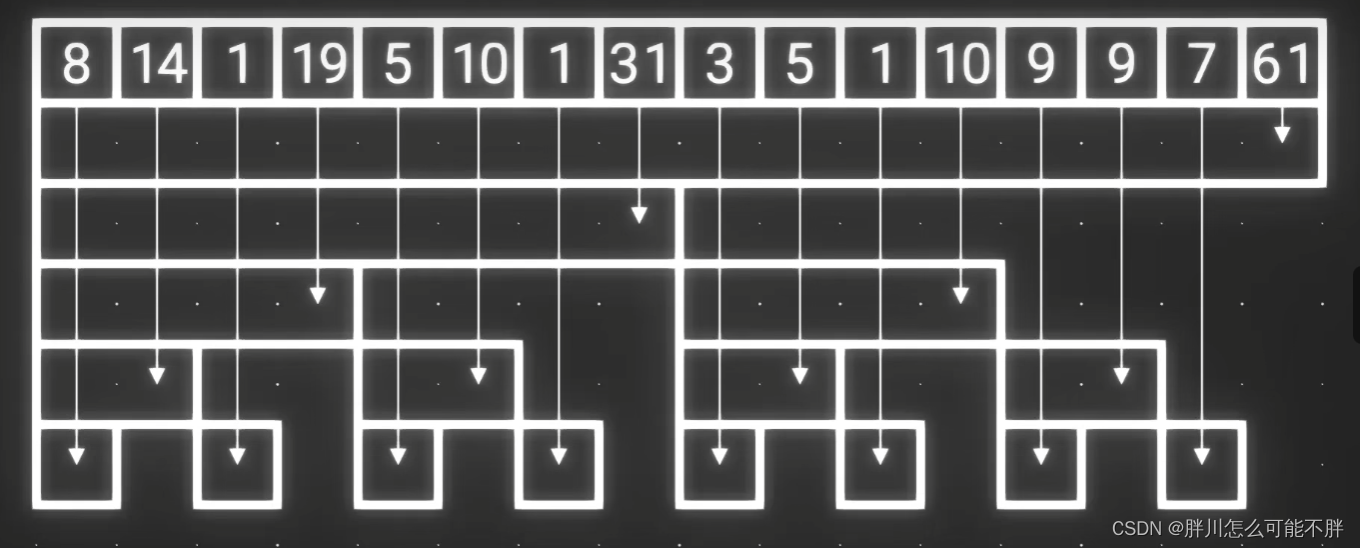
数组中的每一个元素都对应下面的每一个去区间，而下面每一个区间又表示为原数组的某个区间和，求和时只要找到某个对应的区间相加就能得到答案，修改区间的时候也只要向上找到包含该数据的区间修改即可

lowbit函数

lowbit函数，查找二进制数字最低为的数字，原理就是取反然后再进行与处理。

int lowbit(int x)
{return x & -x;
}

数组数组的查找和更改

为什么要介绍lowbit函数，是因为在树状数组中（下标从1开始），序号为i的序列正好就是长度为lowbit（i）且以i结尾的序列

因此查找的时候，就可以不断地找i-lowbit（i）的数组相加就能得到答案，区间查找的道理也是这样

void findd(int l, int r)
{sum = 0;for (int i = r;i;i -= lowbit(i))sum += arr[i];for (int i = l-1;i;i -= lowbit(i))sum -= arr[i];
}

如果要更改的话，因为在一个树状数组中arr[i]上面那个数组就是arr[i+lowbit(i)],因此在修改的时候直接向上查找并且都加上修改值就能解决了

void add(int x, int k)
{for (int i = x;i <= n;i += lowbit(i))arr[i] += k;
}

参考资料

练手题目

ac代码：

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include 
#include
#include
#include
#define dbug cout<<"hear!"<=b;i--)
#define pper(a,b) for(ll j=a;j>=b;j--)
#define no cout<<"NO"<,greater >q;
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair PII;
const int N = 2e5 + 100;
const int  INF = 0x3f3f3f3f;
ll gcdd(ll a, ll b)
{if (b) while ((a %= b) && (b %= a));return a + b;
}
ll h[N], ne[N], w[N], to[N], idx;
void add(int a, int b, int c)
{to[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
const int mod = 998244353;
int t, n, m, a, b, c,d, x,y, k, cnt, ans, ant, sum,q, p;
int arr[N], brr[N], crr[N];
int mp[2500][2500];int lowbit(int x)
{return x & -x;
}void add(int x, int k)
{for (int i = x;i <= n;i += lowbit(i))arr[i] += k;
}void findd(int l, int r)
{sum = 0;for (int i = r;i;i -= lowbit(i))sum += arr[i];for (int i = l-1;i;i -= lowbit(i))sum -= arr[i];
}int main()
{cin >> n >> m;rep(1, n){cin >> x;add(i, x);}while (m--){cin >> a >> b >> c;if (a == 1){add(b, c);}else{findd(b, c);cout << sum << endl;}}
}

词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：尚硅谷Docker实战（教程天花板）- 基础篇（零基小白）

下一篇：HCIP复习2

关于树状数组

引入

树状数组介绍

lowbit函数

数组数组的查找和更改

相关内容

热门资讯